概念
定義(1)
 微分方程
微分方程常微分方程與偏微分方程的總稱。含自變數、未知函式和它的微商(或偏微商)的方程稱為常(或偏)微分方程。未知函式為一元函式的微分方程,稱為常微分方程。未知函式為多元函,從而出現多元函式的偏導數的方程,稱為偏微分方程。
定義(2)
微分方程中所出現的未知函式的導數或微分的最高階數稱為微分函式的階。滿足微分方程的函式稱為微分方程的解。求一個微分方程的解的過程稱為解微分方程。
定義(3)
如果常微分方程的解中含有獨立的任意常數(“獨立”指不能將不同的常數合併),且獨立的任意常數的個數與方程的階相同,則這樣的解稱為方程的通解;不含任意常數的解稱為特解。
由通解確定通解時,通常需要一些函式值和導數值,這些已知的函式值和導數值稱為方程的初值或初始條件,把微分方程和其初值合到一起,稱為微分方程的初始問題。
n階微分方程的初值問題的一般形式為
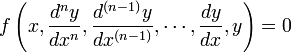 微分方程的基本形式
微分方程的基本形式來源歷史
微分方程研究的來源:它的研究來源極廣,歷史久遠。I.牛頓和G.W.萊布尼茨創造微分和積分運算時,指出了它們的互逆性,事實上這是解決了最簡單的微分方程 y┡=ƒ(x)的求解問題。當人們用微積分學去研究幾何學、力學、物理學所提出的問題時,微分方程就大量地湧現出來。
20世紀以來,隨著大量的邊緣科學諸如電磁流體力學、化學流體力學、動力氣象學、海洋動力學、地下水動力學等等的產生和發展,也出現不少新型的微分方程(特別是方程組)。70年代隨著數學向化學和生物學的滲透,出現了大量的反應擴散方程。
從“求通解”到“求解定解問題” 數學家們首先發現微分方程有無窮個解。常微分方程的解會含有一個或多個任意常數,其個數就是方程的階數。偏微分方程的解會含有一個或多個任意函式,其個數隨方程的階數而定。命方程的解含有的任意元素(即任意常數或任意函式)作儘可能的變化,人們就可能得到方程所有的解,於是數學家就把這種含有任意元素的解稱為“通解”。在很長一段時間裡,人們致力於“求通解”。但是以下三種原因使得這種“求通解”的努力,逐漸被放棄。第一,能求得通解的方程顯然是很少的。在常微分方程方面,一階方程中可求得通解的,除了線性方程、可分離變數方程和用特殊方法變成這兩種方程的方程之外,為數是很小的。如果把求通解看作求微商及消去法的某一類逆運算,那么,也和熟知的逆運算一樣,它是帶試探性而沒有一定的規則的,甚至有時是不可能的(J.劉維爾首先證明黎卡提方程不可能求出通解),何況這種通解也是隨著其自由度的增多而增加其求解的難度的。第二,當人們要明確通解的意義的時候(在19世紀初葉分析奠基時期顯然會考慮到此問題)就會碰到嚴重的含糊不清之處,達布在他的教學中經常提醒大家注意這些困難。這主要發生在偏微分方程的研究中。第三,微分方程在物理學、力學中的重要套用,不在於求方程的任一解,而是求得滿足某些補充條件的解。A.-L.柯西認為這是放棄“求通解”的最重要的和決定性的原因。這些補充條件即定解條件。求方程滿足定解條件的解,稱之為求解定解問題。早期由於外彈道學的需要,以及40年代由於高速氣動力學研究激波的需要,擬線性一階雙曲組的間斷解的研究更得到了重大發展,蘇聯和美國學者作出了貢獻。泛函分析和偏微分方程間的相互聯繫,相互促進發展,首先應歸功於法、波、蘇等國學者的努力。
中華人民共和國建立後,微分方程得到了重視和發展。培養了許多優秀的微分方程的工作者,在常微分方程穩定性、極限環、結構穩定性等方面做出了很多有水平的結果;在偏微分方程混合型刻畫滲流問題的擬線性退縮拋物型、橢圓組和擬線性雙曲組的間斷解等方面做出了很多有水平的結果。
分類
微分方程可分為以下幾類,而隨著微分方程種類的不同,其相關研究的方式也會隨之不同。
常微分方程及偏微分方程
 微分方程
微分方程f\left(x,\frac{d^ny}{dx^n},\frac{d^{(n-1)}y}{dx^{(n-1)}},\cdots,\frac{dy}{dx},y\right)=0
常微分方程常依其階數分類,階數是指自變數導數的最高階數:p.3,最常見的二種為一階微分方程及二階微分方程。例如以下的貝塞爾方程:
x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}+(x^2-\alpha^2)y=0
(其中y為應變數)為二階微分方程,其解為貝塞爾函式。
偏微分方程(PDE)是指一微分方程的未知數是多個自變數的函式 ,且方程式中有未知數對自變數的偏微分。偏微分方程的階數定義類似常微分方程,但更細分為橢圓型、雙
 微分方程
微分方程\frac{\partialu}{\partialt}+t\frac{\partialu}{\partialx}=0。
線性及非線性
常微分方程及偏微分方程都可以分為線性及非線性二類。
若微分方程中沒有出現未知數及微分項的平方或其他乘積項,也沒有出現未知數及其微分項的乘積,此微分方程為線性微分方程,否則即為非線性微分方程。
齊次線性微分方程是線性微分方程中更細的分類,微分方程的解乘上一係數或是與另一個解相加後的結果仍為微分方程的解。
若線性微分方程的係數均為常數,則為常係數線性微分方程。常係數線性微分方程可以利用拉氏轉換轉換為代數方程:p.315-316,因此簡化求解的過程。
針對非線性的微分方程,只有相當少數的方法可以求得微分方程的解析解,而且這些方法需要微分方程有特別的對稱性。長時間時非線性微分方程可能會出現非常複雜的特性,也可能會有混沌現象。有關非線性微分方程的一些基本問題,例如解的存在性、唯一性及初始值非線性微分方程的適定性問題,以及邊界值非線性微分方程都是相當難的問題,甚至針對特定非線性微分方程的上述基本問題都被視為是數學理論的一大突破。例如2000年提出的7個千禧年大獎難題中,其中一個是納維-斯托克斯存在性與光滑性,都是探討納維-斯托克斯方程式其解的數學性質,至2012年8月為止此問題尚未被證明。
線性微分方程常常用來近似非線性微分方程,不過只在特定的條件下才能近似。例如單擺的運動方程為非線性的微分方程,但在小角度時可以近似為線性的微分方程。
舉例
以下是常微分方程的一些例子,其中u為未知的函式,自變數為x,c及ω均為常數。
非齊次一階常係數線性微分方程:
\frac{du}{dx}=cu+x^2.
齊次二階線性微分方程:
\frac{d^2u}{dx^2}-x\frac{du}{dx}+u=0.
描述諧振子的齊次二階常係數線性微分方程:
\frac{d^2u}{dx^2}+\omega^2u=0.
非齊次一階非線性微分方程:
\frac{du}{dx}=u^2+1.
描述長度為L的單擺的二階非線性微分方程:
L\frac{d^2u}{dx^2}+g\sinu=0.
以下是偏微分方程的一些例子,其中u為未知的函式,自變數為x及t或者是x及y。
齊次一階線性偏微分方程:
\frac{\partialu}{\partialt}+t\frac{\partialu}{\partialx}=0.
拉普拉斯方程,是橢圓型的齊次二階常係數線性偏微分方程:
\frac{\partial^2u}{\partialx^2}+\frac{\partial^2u}{\partialy^2}=0.
KdV方程,是三階的非線性偏微分方程:
\frac{\partialu}{\partialt}=6u\frac{\partialu}{\partialx}-\frac{\partial^3u}{\partialx^3}。
性質
普遍性的數學描述許多物理或是化學的基本定律都可以寫成微分方程的形式。在生物學及經濟學中,微分方程用來作為複雜系統的數學模型。微分方程的數學理論最早是和方程對應的科學領域一起出現,而微分方程的解就可以用在該領域中。不過有時二個截然不同的科學領域會形成相同的微分方程,此時微分方程對應的數學理論可以看到不同現象後面一致的原則。
例如考慮光和聲音在空氣中的傳播,以及池塘水面上的波動,這些都可以用同一個二階的偏微分方程來描述,此方程即為波動方程,因此可以將光和聲音視為一種波,和水面上的水波有些類似之處。約瑟夫·傅立葉所發展的熱傳導理論,其統御方程是另一個二階偏微分方程-熱傳導方程式,擴散作用看似和熱傳導不同,但也適用同一個統御方程,而經濟學中的布萊克-休斯方程也和熱傳導方程有關。
微分方程的解通常是一個函式表達式y=f(x)\,(含一個或多個待定常數,由初始條件確定)。例如:
\frac{dy}{dx}=\sinx,的解是y=-\cosx+C,其中C是待定常數;
例如,如果知道y=f(\pi)=2,則可推出C=1,而可知y=-\cosx+1,
一階線性常微分方程
對於一階線性常微分方程,常用的方法是常數變易法:
對於方程:y'+p(x)y+q(x)=0
可知其通解:y=C(x)e^{-\intp(x)\,dx}
然後將這個通解代回到原式中,即可求出C(x)的值
二階常係數齊次常微分方程
對於二階常係數齊次常微分方程,常用方法是求出其特徵方程的解
對於方程:y''+py'+qy=0
可知其通解:y=c_1y_1+c_2y_2
其特徵方程:r^2+pr+q=0
根據其特徵方程,判斷根的分布情況,然後得到方程的通解
一般的通解形式為(在\begin{smallmatrix}r_1=r_2\end{smallmatrix}
的情況下):y=(C_1+C_2x)e^{rx}
(在\begin{smallmatrix}r_1\ner_2\end{smallmatrix}的情況下):y=C_1e^{r_1x}+C_2e^{r_2x}
(在共軛複數根的情況下):y=e^{\alphax}(C_1\cos(\betax)+C_2\sin(\betax))
約束條件
微分方程的約束條件是指其解需符合的條件,依常微分方程及偏微分方程的不同,有不同的約束條件。
常微分方程常見的約束條件是函式在特定點的值,若是高階的微分方程,會加上其各階導數的值,有這類約束條件的常微分方程稱為初值問題。
若是二階的常微分方程,也可能會指定函式在二個特定點的值,此時的問題即為邊界值問題。若邊界條件指定二點數值,稱為狄利克雷邊界條件(第一類邊值條件),此外也有指定二個特定點上導數的邊界條件,稱為諾伊曼邊界條件(第二類邊值條件)等。
偏微分方程常見的問題以邊界值問題為主,不過邊界條件則是指定一特定超曲面的值或導數需符定特定條件。
解的存在性及唯一性
存在性是指給定一微分方程及約束條件,判斷其解是否存在。唯一性是指在上述條件下,是否只存在一個解。
針對常微分方程的初值問題,皮亞諾存在性定理可判別解的存在性,柯西-利普希茨定理則可以判別解的存在性及唯一性。
針對偏微分方程,柯西-克瓦列夫斯基定理可以判別解的存在性及唯一性。皮亞諾存在性定理可以判斷常微分方程初值問題的解是否存在。
套用
平面二次曲線方程含有五個參數,兩端對x求五次微商,連同原方程共得六個方程,消去參數就得到微分方程
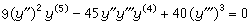 。 (1)
。 (1)
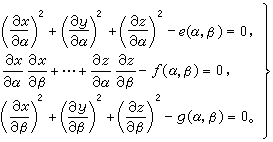 (2)
(2)
幾何學提出的微分方程很多。(J.-)G.達布的《曲面一般理論教程》一直是這方面值得參考的書。
變分學中令積分取極值的必要條件歐拉方程一般是非線性微分方程(或組)。
剛體力學的基本方程就是一個微分方程組。流體力學的基本方程就是所謂納維-斯托克斯方程,彈性力學的方程一般是高階方程。電磁學提出了著名的拉普拉斯方程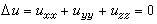 ,光學和聲學提出了波動方程
,光學和聲學提出了波動方程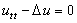 ,熱學提出了熱傳導方程
,熱學提出了熱傳導方程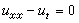 ,量子力學中提出了薛丁格方程
,量子力學中提出了薛丁格方程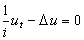 。
。
發展過程
從理論上講,若已知方程的通解,則只需選擇其中的任意元素使之滿足定解條件即可得出定解問題的解。而實際上這種選擇往往是非常難的,更不用說求得通解的困難了。相反地,如果把出現在定解條件中的數據或多或少地變動一下都能求得方程的一個解,那么把這些數據作儘可能地變動時就可能求得方程所有的解即通解。就是採取了這種觀點,柯西和K.(T.W.)外爾斯特拉斯幾乎同時證明了常微分方程通解的存在性,而偏微分方程也從此得到了迅速的發展。定解問題的定義和要求方程(或稱泛定方程)
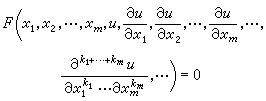
是加在含m個自變數x1,x2,…,xm的未知函式u及其各階偏微商上的一個關係,即若把u和由它而得的它的各階偏微商(至少是方程中出現的)都代入F中,則所得結果對於Rm 中的某區域Ωm的所有內點x1,x2,…,xm來說,都要求恆等於零;但對於Ωm的邊界點來說,並不作這樣的要求。
至於定解條件當xm=0時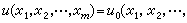
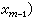 則是在Rm 中(m-1)維流形xm=0上被滿足的。這時,xm=0就稱為支柱。xm=0有時是Ωm中的一個(m-1)維流形,有時就是Ωm的邊界дΩm或дΩm的一部分。所謂當xm=0時有
則是在Rm 中(m-1)維流形xm=0上被滿足的。這時,xm=0就稱為支柱。xm=0有時是Ωm中的一個(m-1)維流形,有時就是Ωm的邊界дΩm或дΩm的一部分。所謂當xm=0時有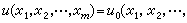
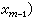 ,就是在Ωm 內當xm=0附近任一點沿任一曲線趨近於xm=0上任一點(x嬼,x嬽,…,x圛)時,u趨近於u0(x嬼,x嬽,…,x圛)。在這種理解下,P.班勒衛指出了這時u0(x1,x2,…,xm-1)應是連續的。定解條件
,就是在Ωm 內當xm=0附近任一點沿任一曲線趨近於xm=0上任一點(x嬼,x嬽,…,x圛)時,u趨近於u0(x嬼,x嬽,…,x圛)。在這種理解下,P.班勒衛指出了這時u0(x1,x2,…,xm-1)應是連續的。定解條件
當xm=0時,
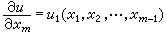
當然也應是在Rm 中一(m-1)維流形xm=0上被滿足的。這時,xm=0仍被稱為支柱,但對微商取值的理解有兩種:一是把它看作當xm趨近於0時
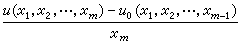
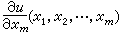 當 xm趨近於0時的極限。顯然,若第二種理解成立則第一種理解必然成立。反之則不盡然。應該指出,也可以用
當 xm趨近於0時的極限。顯然,若第二種理解成立則第一種理解必然成立。反之則不盡然。應該指出,也可以用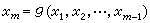 或
或 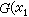 ,
,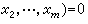 或更一般地用 Rm 中任何一個(m-1)維流形來代替xm=0,它們這時也都被稱為支柱。對函式取值和微商取值若要作上述理解,還需對支柱作必要的正規要求,例如支柱至少是一個若爾當流形等等。
或更一般地用 Rm 中任何一個(m-1)維流形來代替xm=0,它們這時也都被稱為支柱。對函式取值和微商取值若要作上述理解,還需對支柱作必要的正規要求,例如支柱至少是一個若爾當流形等等。由於一階常微分方程的一般形式是F(x,y,y┡)=0,要套用柯西定理,就必需套用隱函式理論解出y┡。在不滿足隱函式定理的條件的情況,常常就是產生奇解的情況。克萊羅方程就是一個最簡單的例子。定解問題研究的開展,大大幫助了對奇解的了解。
柯西提出定解問題的時代也是複變函數論開始蓬勃發展的時代,“兩個實域真理間的最短途徑時常是通過一個復真理的”影響,這是當時特別流行的說法,復域裡常微分方程理論(即復解析理論)得到了發展。從推廣柯西定理的布里奧-布凱定理,從(J.-)H.龐加萊的工作到班勒衛、J.馬爾姆奎斯特等人的工作,最引人注目的是線上性方程方面,從I.L.富克斯的結果開始一直到龐加萊的自守函式理論已很完整。但是在非線性方面顯然沒有取得如此令人滿意的成果,其原因可能是多複變函數的奇點理論和解析開拓尚有待發展。
二階常微分方程的柯西問題
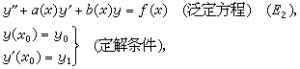
(D1): 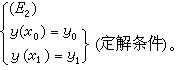
這兩個問題均可歸結為線性積分方程。前者可歸結為第二種沃爾泰拉積分方程,後者則是第二種弗雷德霍姆積分方程。沃爾泰拉方程可以看作弗雷德霍姆方程的特例,但不同的是後者有本徵值、本徵函式問題,而前者沒有。邊值問題和由它而引起的本徵值、本徵函式問題,不僅有理論上的價值,為人們提供很多特殊函式,而且有實用價值(特徵值問題在大型建築中必需考慮到)。
在橢圓型偏微分方程的邊值問題中同樣也引起本徵值和本徵函式問題。
在柯西的倡導下,人們從“求通解”的時代進入了“求解定解問題”的時代,隨著龐加萊的定性理論,常微分方程又從“求解定解問題”的時代進入“求所有解”的時代。
稍後,D.伯克霍夫在動力系統方面開闢了一個新領域。近年來,由於拓撲方法的滲入,更加得到發展。蘇聯Α.М.李亞普諾夫在運動穩定性方面的工作,對天文學、物理學以及工程技術有廣泛套用,極受重視。
此外,在考慮時滯問題時,人們還創立了差分微分方程。近年來,泛函微分方程有很大發展。泛函微分方程是差分微分方程的推廣。
柯西曾把他有關常微分方程方面的結果推廣到一階偏微分方程組的柯西問題,但他在偏微分方程中所考慮的方程並沒有象在常微分方程中所考慮的方程那樣有代表性。因此,後來又引進了模組的概念,柯西和稍後的柯瓦列夫斯卡婭都用長函式法證明了模組柯西問題的解析解是惟一存在的。模的概念顯然依賴於支柱。從而引入了特徵的概念。應特別注意,有些組的特徵表達式A能恆等於零,其中有些方程組是比較重要的,例如方程(2)就是這樣的,廣義相對論的基本方程組也是這樣的。
20世紀初才由霍姆格倫在方程是非重特徵的、係數是解析的、支柱是解析的而非特徵的條件下,證明了解的惟一性。阿達馬指出,只要能在方程是非重特徵的、係數是非解析的、支柱是非特徵的條件下證明霍姆格倫定理,則該定理在方程是非重特徵的、非線性的、非解析的、支柱是非特徵的條件下仍是正確的。至於連續依賴性則並不成立,阿達馬的著名例子
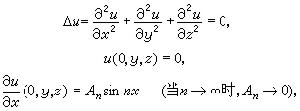
就說明這個問題。
阿達馬分析了他以前和當時的有關線性二階偏微分方程的工作,緊緊抓住“形式相似的方程卻有迥然不同的適定問題”這個矛盾,反覆論證,終於發現了長期未被注意的事實,即柯西-柯瓦列夫斯卡婭定理在方程、支柱和數據有一非解析時是不真的。例如Δu=0在支柱z=0的柯西問題在數據不都是解析時未必是有解的。誠然,雙側的解(即z≤0和z≥0時都存在的解)不存在,因為根據杜恩定理,若存在,則兩個數據必然都是解析的。單側的解也不存在,因為否則用照像法(實際上是一種解析開拓),則雙側解也將存在,但解析方程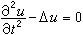 ,解析支柱 t=0、非解析數據的柯西問題卻是實際中提出的,理論證明是適定的。
,解析支柱 t=0、非解析數據的柯西問題卻是實際中提出的,理論證明是適定的。
阿達馬提出了基本解。這不僅是他對前人工作的總結,而且從他本人以前的成就也必然得到這個重要概念。有了基本解,模雙曲型方程的柯西問題的解,只要支柱是空向的,已給數據適當正規,就可以用一個發散積分的有限部分來表示;橢圓型方程就可以形成勢代表解,並通過這個勢滿足的弗雷德霍爾姆型積分方程求得狄里克雷問題的解。間接地求拋物型方程的基本解的步驟也是阿達馬提出來的。他有一句名言:“所有線性偏微分方程問題應該並且可以用基本解來解決。”
在V.沃爾泰拉暗示下,G.F.特里科米進行了混合型方程的所謂特里科米問題的研究。所謂混合型方程,是指在蛻型線L一側是橢圓型,在另一側是雙曲型的方程;1927年特里科米證明了解的存在性。雖然蘇聯學者C.A.洽普雷金在V.沃爾泰拉之前已在射流理論中提出更一般的混合型方程即洽普雷金方程,但只有在40年代由於超音速飛機的製造,在跨音速氣動力學中這類方程才大受重視。M.H.普羅特爾證明了洽普雷金方程特里科米問題的解的惟一性,蘇聯學者A.B.比察澤也在這方面做了大量有意義的工作。由於滲流的研究,促進了擬線性退縮拋物型方程的研究發展,蘇聯學者為此作出了貢獻。
發展中產生的問題
一個方程或方程組的定解問題一旦提出,就產生下列三個問題。
①存在性問題,即這個定解問題是否有解。
②惟一性問題,即其解是否惟一。
③連續依賴性問題,即解是否連續依賴於數據,亦即是否是數據的某階連續泛函。
若定解問題的解是存在的、惟一的、連續依賴於數據的,則這個定解問題稱為適定的。對它就可以進行計算。一般而言,只有適定問題計算才有意義。這樣,微分方程的研究成果才能為實際所套用。
如果對上述三個問題的回答有一個是否定的,這個定解問題就稱為不適定的。一般,不適定問題是原來用來刻畫實際規律的數學模型不恰當,必須另建合適的數學模型。不適定問題也是需要研究的,這種研究有時會導致理論上的新發展。
定解問題研究的發展對常微分方程最早提出的定解問題是柯西問題(C): 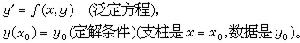
柯西問題(C)是適定的,其根據是柯西定理:若ƒ(x,y)在|x-x0|≤α,|y-y0|≤b上連續,並滿足李普希茨條件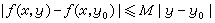 ,則柯西問題(C)在滿足條件
,則柯西問題(C)在滿足條件 下,存在惟一的連續依賴於y0的連續解。由於泛定方程的任一解當x=x0時總要取一個值y0,因此就可以提出柯西問題(C)。由於惟一性,這個柯西問題的解一定就是所考慮的解,所以柯西問題(C)的解就是泛定方程的“通解”。
下,存在惟一的連續依賴於y0的連續解。由於泛定方程的任一解當x=x0時總要取一個值y0,因此就可以提出柯西問題(C)。由於惟一性,這個柯西問題的解一定就是所考慮的解,所以柯西問題(C)的解就是泛定方程的“通解”。
柯西利用L.歐拉早就提出的近似解法(所謂歐拉折線法)證明了當折線邊數無限增加、邊長無限縮小時,這些折線有一極限即(C)的惟一連續依賴於y0的解。這個方法稱為柯西-李普希茨方法。若取消李普希茨條件,則用阿爾澤拉定理仍能證明解的存在性,但不能證明惟一性和連續依賴性。可見李普希茨條件的作用只在於保證解的惟一性。逐次逼近法導源於代數方程近似解法,劉維爾首先把它用於解沃爾泰拉積分方程,(C.-)É.皮卡才把它廣泛套用於解常微分方程柯西問題(C)上,首先把柯西問題變為非線性沃爾泰拉積分方程,然後用逐次逼近法求解,結果完全和歐拉折線法的一樣。
![微分方程[數學分支] 微分方程[數學分支]](/img/8/f98/nBnauM3X3QTM1EjMwQDNwIzNyQTM5IjMwgDMzQTNwAzMwIzL0QzLxczLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg)
