初等常微分方程
常微分方程的通解,粗略地說就是:①它把未知函式y表示為自變數x的顯函式的形式y=φ(x),此函式滿足該微分方程。②在此表達式中含有一些任意常數,其個數恰等於方程的階數。當這些常數任意變動時即能得到方程的所有解,除了少數解是例外。③表達式適用於全空間,或至少不是局部的而是大範圍的。如果在這定義中不要求①成立,即在所得的表達式中未知函式可能是自變數的隱函式形式φ(x,y)=0,則稱此表達式為通積分。通解(或通積分)的嚴格定義,實際上就是進一步把條件②的後半部作嚴格的敘述,即要求:對於該表達式所適用的區域中任意給定的初始條件,必能找到任意常數的一組確定的值,使得這組值所對應的解(或積分)能夠滿足這個初始條件。出現於方程中的變數x、y可以是實變數,也可以是復變數。一個解y=φ(x)或積分φ(x,y)=0在(x,y)空間中的軌跡稱為方程的積分曲線。當(x,y)為實數時,積分曲線就是(x,y)平面上的曲線。當(x,y)為複數(x=x1+ix2,y=y1+iy2)時,積分曲線是四維實空間(x1,x2,y1,y2)中的二維曲面。通解或通積分的軌跡稱為積分曲線族。要求一個解或積分滿足已給的初始條件,就是要求由它所確定的積分曲線通過預先給定的一點。
下面根據方程形式的不同,或階數與個數的不同,分別作簡要的介紹:
可分離變數的方程 形如
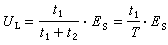 (1)
(1)
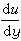
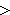 (2)
(2)
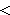 , (3)
, (3)
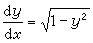 時丟掉的解y=±1不能包含在通解 y=sin(x+C)之中。這一類丟掉的解往往是奇解。所謂奇解就是在其上處處破壞初值問題惟一性的解(見常微分方程初值問題)。
時丟掉的解y=±1不能包含在通解 y=sin(x+C)之中。這一類丟掉的解往往是奇解。所謂奇解就是在其上處處破壞初值問題惟一性的解(見常微分方程初值問題)。 有些看上去是不能分離變數的方程,通過變數代換可以化為可分離變數的方程來求解。最常遇到的是齊次常微分方程
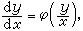 (4)
(4)
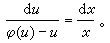
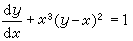 經代換y=x+u,方程
經代換y=x+u,方程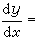
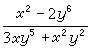 經兩次代換y3=v及v=ux,均可化為可分離變數的方程。不過用這種方法有時並非易事,也並不一定都能辦到。
經兩次代換y3=v及v=ux,均可化為可分離變數的方程。不過用這種方法有時並非易事,也並不一定都能辦到。 一階線性方程 形如
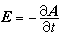 (5)
(5)
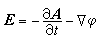 (6)
(6)
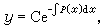 (7)
(7)
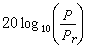 (8)
(8)
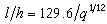 (9)
(9)
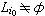 (10)
(10)
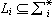 (11)
(11)
有些微分方程可以通過變數代換而化為一階線性方程。最常見的是伯努利方程
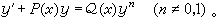 (12)
(12)
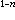 。又如對方程
。又如對方程 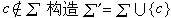 可改用x為未知函式、y為自變數而化為
可改用x為未知函式、y為自變數而化為 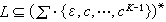 又如
又如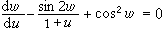 可借變數代換w=arctan v而化為線性方程,等等。
可借變數代換w=arctan v而化為線性方程,等等。 黎卡提方程及其他 在常微分方程的發展史上,黎卡提方程
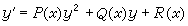 (13)
(13)
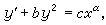 (14)
(14)
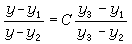
復變數的黎卡提方程在常微分方程解析理論中也有它的重要性,因為它是只可能有動極點而無動支點的方程,此外,它還和微分幾何學與複變函數論中的一些重要問題有密切關係。
熟知的可積類型還有:①雅可比方程
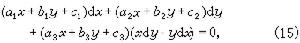
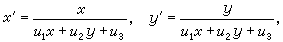
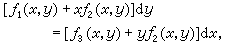 (16)
(16)
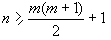 個特解為已知時,它是可積分的。③第一類阿貝爾方程
個特解為已知時,它是可積分的。③第一類阿貝爾方程 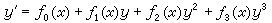
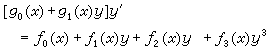
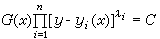 (17)
(17)
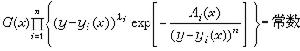
恰當方程與積分因子 滿足條件
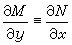 (18)
(18)
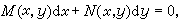 (19)
(19)
當條件(18)不滿足時,如果能找到函式 μ(x,y) 使
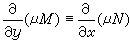
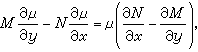 (20)
(20)
(20)是關於μ(x,y)的一階線性偏微分方程,求它的通解比求(19)的通解困難。但當M、N滿足一定的條件時可以只求(20)的一個一元函式特解。例如,若
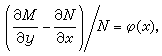 (21)
(21)
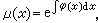
 等形狀的積分因子時所應滿足的條件。
等形狀的積分因子時所應滿足的條件。 易見方程(1)實際上是借積分因子
 而被化為恰當方程(2),方程(5)滿足條件(21),故有積分因子
而被化為恰當方程(2),方程(5)滿足條件(21),故有積分因子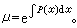 又當(19)為齊次方程且xM+yN扝0時有積分因子
又當(19)為齊次方程且xM+yN扝0時有積分因子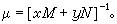
一階隱方程 形如
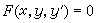 (22)
(22)
若(22)可就y┡解得若干個一階顯方程
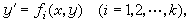 (23)
(23)
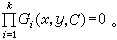
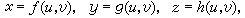
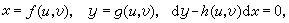
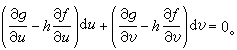 (24)若
(24)若
在求解(22)時,常記y┡為p,且以p為參數來表達積分曲線族的方程。若由(22)可解得y=ƒ(x,p)或x=φ(y,p),取x、p(或y、p)為參數即可把(22)化成(24)的形式。又若(22)取特殊形式
 (25)
(25)
如果存在常數k,使(22)中的函式F能滿足

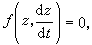 即(25)的前一方程的形式。顯然當k=1時(22)是比(4)更廣的齊次一階隱方程。
即(25)的前一方程的形式。顯然當k=1時(22)是比(4)更廣的齊次一階隱方程。 一階隱方程中,特別重要的是克萊羅方程
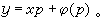 (26)
(26)
有時對方程(22)可使用勒讓德變換Χ=y┡, Y=xy┡-y將方程變形。此變換的逆變換也具有同樣的形式:
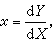
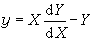 ;稱為對稱原理。當兩方程F(x,y,p)=0與F(P,ΧP-Y,Χ)=0中的任一個可求積時,另一方程的通解便可借代數方法由前一方程的通解導出。這種變換在微分方程的理論研究中也很有用處。
;稱為對稱原理。當兩方程F(x,y,p)=0與F(P,ΧP-Y,Χ)=0中的任一個可求積時,另一方程的通解便可借代數方法由前一方程的通解導出。這種變換在微分方程的理論研究中也很有用處。 對於方程(22),由F(x,y,p)=0及
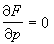 消去p得到的關係式φ(x,y)=0,稱為(22)的p-判別式。設(22)的通積分為φ(x,y,с)=0, 則由φ(x,y,с)=0及
消去p得到的關係式φ(x,y)=0,稱為(22)的p-判別式。設(22)的通積分為φ(x,y,с)=0, 則由φ(x,y,с)=0及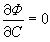 消去C而得到的關係式ψ(x,y)=0稱為(22)的C-判別式。如果(22)的奇解或積分曲線族的包絡存在的話,其方程必同時含於p-判別式和C-判別式之中,但其逆不一定成立。一個典型的例子是
消去C而得到的關係式ψ(x,y)=0稱為(22)的C-判別式。如果(22)的奇解或積分曲線族的包絡存在的話,其方程必同時含於p-判別式和C-判別式之中,但其逆不一定成立。一個典型的例子是 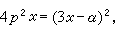 (27)
(27)
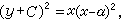 C-判別式為x(x-α)=0,p-判別式為
C-判別式為x(x-α)=0,p-判別式為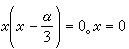 是奇解,也是積分曲線族的包絡。但x=α是結點軌跡,不是(27)的解;
是奇解,也是積分曲線族的包絡。但x=α是結點軌跡,不是(27)的解;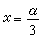 是切點軌跡,也不是(27)的解。若α=0,則x=0成為積分曲線族
是切點軌跡,也不是(27)的解。若α=0,則x=0成為積分曲線族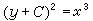 的尖點軌跡,它也不是方程4p2=9x的解。
的尖點軌跡,它也不是方程4p2=9x的解。 高階方程 一般形式為
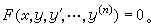 (28)
(28)
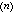 =ƒ(x),對 x積分n次即得通解。②y″=ƒ(y),此方程有明顯的物理學意義。以 2dy乘之,積分,得:
=ƒ(x),對 x積分n次即得通解。②y″=ƒ(y),此方程有明顯的物理學意義。以 2dy乘之,積分,得: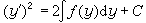 它表示能量守恆律,再積分即得通解。③F(x,y
它表示能量守恆律,再積分即得通解。③F(x,y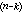 ,…,y
,…,y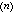 )=0可借代換z=y
)=0可借代換z=y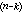 降階k次。④F(y,y┡,…,y
降階k次。④F(y,y┡,…,y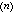 )=0,可改取y為自變數,y┡=p為未知函式而降階一次。⑤ F(x,y
)=0,可改取y為自變數,y┡=p為未知函式而降階一次。⑤ F(x,y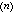 )=0,若能找到方程的參數表示式x=φ(t),y
)=0,若能找到方程的參數表示式x=φ(t),y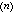 =ψ(t),便可將y
=ψ(t),便可將y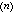 逐次對x積分而得出通解的參數表示式。⑥若F 對 y,y┡,…,y
逐次對x積分而得出通解的參數表示式。⑥若F 對 y,y┡,…,y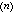 為齊次函式,即F(x,ty,…,ty
為齊次函式,即F(x,ty,…,ty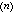 )=tmF(x,y,…,y
)=tmF(x,y,…,y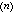 ),則可借代換z=y┡/y而把(28)降階一次。⑦像一階恰當方程一樣,(28)有時也可表為
),則可借代換z=y┡/y而把(28)降階一次。⑦像一階恰當方程一樣,(28)有時也可表為 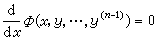
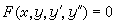 (29)
(29)
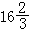 且M、N滿足條件(18),則(29)即為恰當方程。特別,二階線性方程 y″+p(x)y┡+q(x)y+r(x)=0,當q(x)=p┡(x)時為恰當方程。
且M、N滿足條件(18),則(29)即為恰當方程。特別,二階線性方程 y″+p(x)y┡+q(x)y+r(x)=0,當q(x)=p┡(x)時為恰當方程。 方程組的初等積分法 方程組
 (30)
(30)
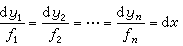
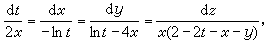 (31)
(31)
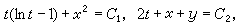
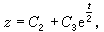 它和前兩個首次積分一起就構成(31)的通積分。有時用不同的方法可得不同的首次積分,但可證明(30)的獨立的首次積分最多只有 n個。又若能用上述方法求得(30)的k個獨立的首次積分,就可以利用它們來把(30)降為只 含n-k個未知函式的方程組。一般,由實際問題導出的方程組要想用初等積分來求得通解往往是辦不到的。例如在天體力學中,由三體問題建立的一階方程組含有18個方程,而人們只能找到它的10個獨立的首次積分。即使對平面限制性圓形三體問題的最簡單情況,通積分也還未求出來。
它和前兩個首次積分一起就構成(31)的通積分。有時用不同的方法可得不同的首次積分,但可證明(30)的獨立的首次積分最多只有 n個。又若能用上述方法求得(30)的k個獨立的首次積分,就可以利用它們來把(30)降為只 含n-k個未知函式的方程組。一般,由實際問題導出的方程組要想用初等積分來求得通解往往是辦不到的。例如在天體力學中,由三體問題建立的一階方程組含有18個方程,而人們只能找到它的10個獨立的首次積分。即使對平面限制性圓形三體問題的最簡單情況,通積分也還未求出來。