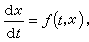常微分方程初值問題
正文
求常微分方程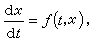
(1)
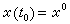(2)
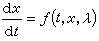時，解同參數λ有何依賴關係；等等。初值問題是A.-L.柯西於19世紀30年代首先提出的,所以又叫柯西問題。在這之前，求解常微分方程是企圖求其通解，但能夠求出通解的只是一些特殊的方程，而在力學和物理學中出現的大多數方程都無法求出通解。柯西從另一種觀點考慮，提出了初值問題，並採用優函式方法，在函式ƒ(t,x)於點(t0,x0)的某個鄰域裡解析的條件下第一次證明了初值問題 (1)+(2)的解析解的存在惟一性。所謂優函式是指：若ƒ(t,x)、F(t,x)均在點(t0,x0)的某一鄰域內解析，設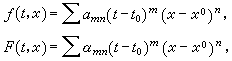 
為簡單起見,以下沒有特別指明之處，都是對n=1的情況而言的，但所有結論對一般的n都成立。
解的存在性 初值問題(1)+(2)並非都有解存在。例如，初值問題
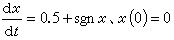的解就不存在。甚至有的方程在它右端函數定義域上的任何一點都無解存在。例如方程 
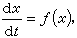其中當x為無理數時ƒ(x)=0,當x為有理數時 ƒ(x)=1，就是如此。初值問題有解存在的基本定理是柯西-皮亞諾存在定理:若ƒ(t,x)在矩形域R(│t-t0│≤α│x-x0│≤b)上連續,則初值問題(1)+（2）在區間│t-t0│≤h上至少存在一個解x(t)。在這裡,
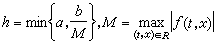,（圖1）。 
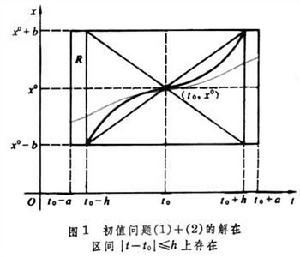常微分方程初值問題
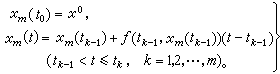(3)
解的開拓性 柯西－皮亞諾存在定理描述的是解在t0附近的一個區間上的存在性，因而是一個局部性的定理。若 ƒ（t，x）在某一平面有界區域 G上連續，G 可能很大，這時，可以用如下方法把在小區間上有定義的解開拓到較大的區間上去。適當地選取 α0、b0> 0，作
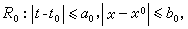使R0嶅G，則過點（t0,x0）至少有方程（1）的一個解x（t）在區間│t-t0│≤h0上存在。其中 
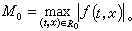令
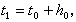
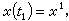顯然,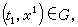
則又可適當地選取α1b1>0，作R1:
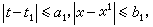使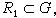
於是可向右邊開拓到區間 t1≤t≤t1+h1上(見圖2
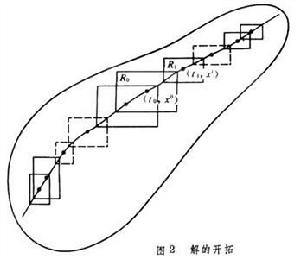)。如此繼續下去，可一直開拓到G的邊界嬠G的任何鄰近。同樣,也可將解 x(t)從點(t0-h0，x(t0-h0))向左邊開拓。如此經開拓而得的解稱為方程(1)過點(t0,x0)的飽和解。飽和解的定義區間稱為解的最大存在區間;它必為開區間。綜上所述有開拓定理:設ƒ(t,x)在平面有界開域G上連續,設x(t)為(1)的任一解（或積分曲線）,其最大存在區間為(с,d)，則必有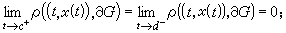 
當G無界時,G上的積分曲線或是開拓到無限接近G的境界線，或者趨向無窮遠。但在接近於G的境界線時,可能是振動的。事實上，不管G是有界還是無界，如果將G的無窮遠處也理解為其邊界，那么方程(1)過G中任一點的積分曲線必可開拓到G的邊界。因此,下面的結論總是成立的：
設x(t)的最大存在區間是(α,b),則t→α+或t→b－時有
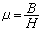(4)
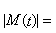
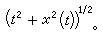
解的惟一性 ƒ(t,x) 的連續性不能保證初值問題(1)+(2)的解惟一。例如方程
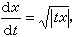其右端函式在整個平面R2上定義且連續，但過點(0，0)的解至少有兩個：x1(t)=0 和
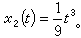實際上這時有無限個解通過這個點(圖3
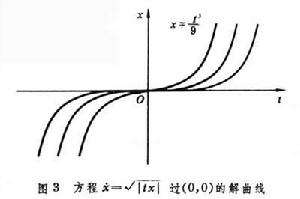)，形成過點(0,0)的一束解(稱其為皮亞諾束)。這是平面情形。對一般的n,若方程(1)在域
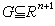上過點(t0,x0)的解不惟一,則過此點的積分曲線的全體形成一個漏斗狀的集合，稱為積分漏斗。 惟一性條件 初值問題解的惟一性條件,最常用的是李普希茨條件。設ƒ(t,x)在R:|t-t0|≤α,│x-x0│≤b上連續,存在常數K 使
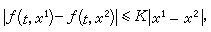當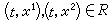
時,則說ƒ（t,x）在R上滿足李普希茨條件。此外,常見的還有奧斯古德條件: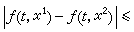
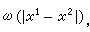當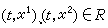
時。 其中ω(r)在r≥0上非負連續,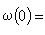
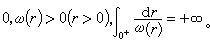還有卡姆克條件: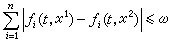
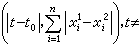
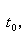當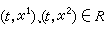
時。 其中ω(t,r)是 0<t<α,r≥0上的連續非負函式,對任何α∈(0,α),在0≤t≤α上連續可微的函式 r(t)呏0是滿足方程
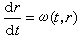及條件r(0)=妝+(0)=0在區間0<t≤α上的惟一解。 如果ƒ(t,x)滿足這些惟一性條件,則方程(1)只能有一個滿足初值條件 (2)的解(惟一性定理)。這個定理可以用比較原理給以證明。在李普希茨條件下，解的存在性可以作皮卡逐步逼近序列 {xm(t)}於│t-t0│≤h上一致收斂於此解來證明。這些惟一性條件只保證解的局部惟一性。但只要ƒ在域G中每一點都滿足惟一性條件，則方程(1)過G中任一點的飽和解都是惟一的。惟一性的討論已有一百多年的歷史，至今仍有人在研究，並相繼提出了許多惟一性條件。
解對初值和參數的相依性 在套用初值問題描述一個物理過程時,由於初值和方程(1)的右端函式通常由實驗測定，而小的測量誤差可能引起解的很大變化，因此在套用中（如在變分法和最優控制等學科中），就需要考察初值和參數變化時解的變化規律。於是解對初值和參數的依賴關係在理論上和套用上都很重要。
考慮帶參數的常微分方程
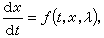(1)λ
解對初值和參數連續的一般定理 設 ƒ（t,x,λ）在G×Iλ上連續,關於x滿足李普希茨條件,即存在常數K>0，使
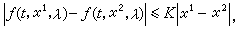那么對每個(t0，x0)∈G,λ∈Iλ,存在通過(t0,x0)的 惟一解 x=φ(t,t0,x0,λ),其定義域是R1×G×Iλ中的開集E,在E上φ(t,t0,x0,λ)是連續的。這個定理只表明過點（t0,x0）的解在定義區域內是連續的，但並沒有反映當初值和參數變化時解在 t的定義區間上整體的變化情況。下面的定理指出了對某個大範圍內的t,解對初值和參數連續是一致的。 解對初值和參數的整體連續性定理 設ƒ(t,x,λ)滿足上述定理的條件,又設x＝ψ(t)是方程(1)λ當λ=憳 時的解，其最大存在區間為(с,d)。對任一閉子區間【α,b】嶅（с,d），存在δ>0，使當
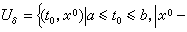
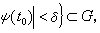
時,對任意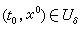
和λ∈(憳-δ,憳+δ)，則方程(1)λ的惟一解φ（t,t0,x0,λ）至少在【α,b】上有定義，且是變數t，t0，x0，λ在區域【α,b】×Uδ×（憳-δ，憳+δ）上的連續函式。並且對任意慪∈【α,b】，當
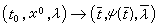時,φ(t,t0,x0,λ)→ψ(t) 對 t∈【α,b】一致成立。對任意 ε>0，存在δ>0，使當│x0- ψ(t0)|<δ，|λ-憳|<δ時有 |φ(t,t0,x0,λ)-ψ(t)│<ε,t∈【α,b】。 上述兩定理中，ƒ（t，x，λ）關於x滿足李普希茨條件，目的是保證解的惟一性。事實上，只要初值問題(1)λ+(2)的解是惟一的，那么上面兩定理仍然成立。
解對初值和參數的可微性定理 設ƒ（t,x，λ）在G×Iλ內關於(x，λ)連續可微，那么初值問題(1)λ+(2)的解x＝φ(t,t0,x0,λ)作為變數(t,t0,x0,λ)的函式在其定義域內連續可微。
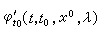和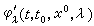
作為t的函式分別滿足初值問題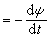
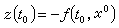和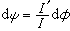
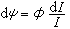
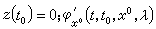作為t的函式滿足矩陣微分方程的初值問題
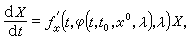Χ(0)=E。E為n×n單位矩陣。 在上面三個定理中，固定 λ時，就分別得到解對初值的有關依賴性定理。
初值問題的推廣 當ƒ(t,x)連續時，就能保證牛頓解的存在性，但在實際套用中出現了ƒ(t,x)為不連續的情形，這類方程已成為現代微分方程理論研究的一個重要課題。前面已有例子表明，ƒ(t,x)不連續時，不一定有牛頓解存在，因此很有必要推廣解的概念。到目前為止，已有多種解的推廣，下面簡述常遇到的卡拉西奧多里解的概念和一個存在性定理。設 φ(t)是區間I上的絕對連續函式，對t∈I上除了一個測度為零的集合外，滿足方程
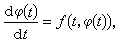則φ(t)稱為方程(1)的卡拉西奧多里解或卡氏解。 卡拉西奧多里存在定理 設ƒ(t,x)在G上定義,對每個固定的x關於t可測，對每個固定的t關於x連續；對任一有界閉域D嶅G，存在勒貝格可積函式 m(t)，使得當(t,x)∈D時 |ƒ(t,x)|≤m(t),則方程(1)存在一個滿足初值條件(2)的卡氏解。當ƒ(t,x)在G上連續時，卡氏解就歸結為牛頓解。
常微分方程初值問題在常微分方程理論的發展中有著重要的作用，在實際套用中也極其重要，在促進某些數學分支的發展中也起了很大的作用。到目前為止，這方面的研究還在進行。
