常微分方程邊值問題數值解法

常微分方程邊值問題數值解法

正文

用某種離散化數值步驟求出常微分方程邊值問題在離散點上的近似解的方法。各種實際問題導出不同類型的邊值問題。較簡單的有二階常微分方程兩點邊值問題：求函式y=y(x)，x∈【α,b】，使它滿足微分方程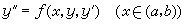

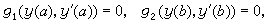
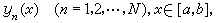
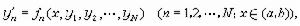
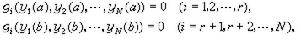
和邊值條件

式中ƒ、g1、g2為已知函式；α與b為兩個給定的端點。較一般地有一階常微分方程組兩點邊值問題:求N個函式

使其滿足微分方程組

和邊值條件

式中諸ƒn、gi是已知函式;r為給定的自然數。有些問題因求解區間是無窮區間而被稱作奇異邊值問題，相應的邊界條件變為對解在無窮遠處漸近行為的限制,例如,要求y(x)在區間【0，)上平方可積或要求當x趨於無窮時，y(x)趨於某極限值。還有些實際問題因要求解滿足多個點上的條件而被稱作多點邊值問題。近年來，對反映邊界層現象的奇異攝動邊值問題提出了一些新的數值解法。此外，關於存在多個解的分歧現象數值解問題也引起人們的注意。
解常微分方程邊值問題常用的數值解法有差分法和打靶法。
差分法　主要步驟是：將區間【α,b】作剖分

把微分方程差分離散化（見數值微分），加上邊值條件一併構成一代數方程組，解此代數方程組即可得到邊值問題的數值解。
打靶法　主要思路是:適當選擇和調整初值條件,求解一系列初值問題，使之逼近給定的邊界條件。如果將描述的曲線視作彈道，那么求解過程即不斷調整試射條件使之達到預定的靶子,所以稱作打靶法或試射法,此類方法的關鍵是設計選取初值的步驟。對非線性邊值問題

可通過下列步驟求數值解： ①計算初值問題

的數值解y1。若g(y1(b),y姈(b))=B,近似地滿足，則y1即為所求；否則進行②。 ②計算初值問題

的數值解y2,若g(y2(b),y娦(b))=B近似地滿足，則y2即為所求；否則令m＝3進行③。
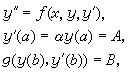
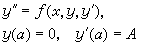
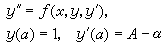
③ 將g(y(b),y┡(b))視為y(α)的函式,用線性逆插值法調整初值，即計算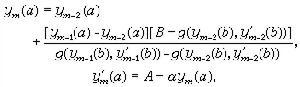然後進行④。 ④計算初值問題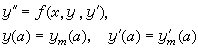

的數值解ym並進行判定：若b點邊值條件近似地滿足,則ym即為所求;否則令m+1崊m轉向③繼續計算直到滿意為止。
特別地，若微分方程是線性的，則打靶法變成線性組合法，即根據常微分方程理論適當選取初值可得到一組線性獨立解，利用它們的線性組合導出邊值問題的解。例如線性方程邊值問題

的數值解可通過兩個初值問題數值解來實現。事實上，設y1(x)和y2(x)分別是方程(1)的具有初值條件和

的兩個解，於是

是(1)與(2)的解。
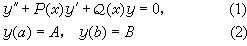
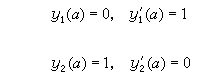
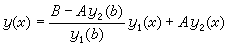
參考書目
　P.Henrici,Discrete variable Methods in Ordinary Differential Equations, John Wiley & Sons,New York,1962.
　S.M.Roberts and J.S.Shipman,Two-Point Boundary value Problems: Shooting Methods,Elsevier, New York,1972.

配圖

相關連線