函式項級數
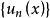 一致收斂
一致收斂 設 是定義在數集I上的函式列,表達式
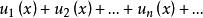 一致收斂
一致收斂 稱為定義在I上的函式項級數,而
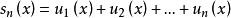 一致收斂
一致收斂 稱為函式項級數的部分和。
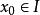 一致收斂
一致收斂 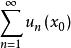 一致收斂
一致收斂 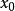 一致收斂
一致收斂 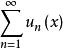 一致收斂
一致收斂 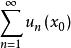 一致收斂
一致收斂 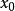 一致收斂
一致收斂 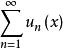 一致收斂
一致收斂 對於每一個 ,如果常數項級數 收斂,則 稱為函式項級數 的收斂點;如果常數項級數 發散,則 稱為函式項級數 的發散點。
定義
 一致收斂
一致收斂  一致收斂
一致收斂  一致收斂
一致收斂 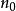 一致收斂
一致收斂 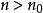 一致收斂
一致收斂 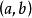 一致收斂
一致收斂  一致收斂
一致收斂 若對任給的正數 ,不論它如何小,常能找到一個只依賴於 但與 無關的數 ,使對 以及區間 中的每一 ,都有
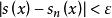 一致收斂
一致收斂 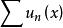 一致收斂
一致收斂 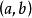 一致收斂
一致收斂 則稱級數 在區間 上一致收斂。
判別法
柯西準則
 一致收斂
一致收斂 函式列 在數集D上一致收斂的充要條件是:
 一致收斂
一致收斂 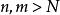 一致收斂
一致收斂 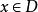 一致收斂
一致收斂 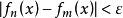 一致收斂
一致收斂 對任給>0,總存在正整數N,使得當 時,對一切 ,都有 。
餘項準則
 一致收斂
一致收斂 函式列 在數集D上一致收斂的充要條件是 :
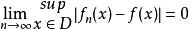 一致收斂
一致收斂 Weierstrass判別法
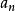 一致收斂
一致收斂 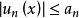 一致收斂
一致收斂 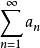 一致收斂
一致收斂 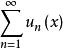 一致收斂
一致收斂 若對充分大的n,恆有實數 ,使得 對E上任意的x都成立,並且數項級數 收斂,則 在E上一致收斂。
Abel判別法
如果
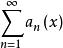 一致收斂
一致收斂 1)函式項級數 在E上一致收斂
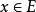 一致收斂
一致收斂 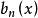 一致收斂
一致收斂 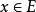 一致收斂
一致收斂 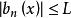 一致收斂
一致收斂 2)對每一固定的 , 隨n而單調,而對任意的 和n,有 (不依賴於x和n的定數)
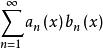 一致收斂
一致收斂 那么 在E上一致收斂。
Dirichlet判別法
如果
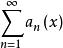 一致收斂
一致收斂 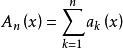 一致收斂
一致收斂 1)函式項級數 的部分和 在E上一致有界
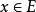 一致收斂
一致收斂 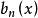 一致收斂
一致收斂 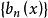 一致收斂
一致收斂 2)對每一 , 隨n而單調,並且函式序列 在E上一致收斂於零
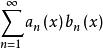 一致收斂
一致收斂 那么 在E上一致收斂。