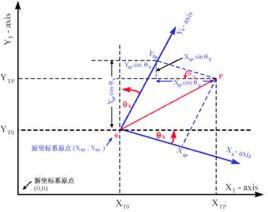
定義
一般定義
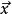 仿射變換
仿射變換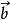 仿射變換
仿射變換一個對向量 平移 ,與鏇轉放大縮小 A的仿射映射為
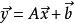 仿射變換
仿射變換上式在齊次坐標上,等價於下面的式子
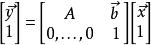 仿射變換
仿射變換在分形的研究里,收縮平移仿射映射可以製造制具有自相似性的分形。
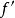 仿射變換
仿射變換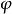 仿射變換
仿射變換 仿射變換
仿射變換一個在兩個仿射空間之間的仿射變換,是在向量上呈現線性之坐標點的變換(即為空間中點與點之間的向量)。以符號表示的話, 使得 ,決定任一對點的線性變換:
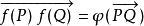 仿射變換
仿射變換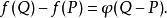 仿射變換
仿射變換或者
其他定義
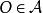 仿射變換
仿射變換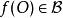 仿射變換
仿射變換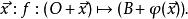 仿射變換
仿射變換. 我們可以將此定義繼續延伸: 假設選定一原點 , 且B表示其圖像 ,如此即代表對任何向量
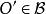 仿射變換
仿射變換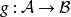 仿射變換
仿射變換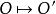 仿射變換
仿射變換假設選定一原點
,此即可以拆解成一仿射變換使得,特定而言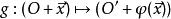 仿射變換
仿射變換總結即,很直觀的, f包含了一個變換與線性坐標。
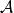 仿射變換
仿射變換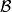 仿射變換
仿射變換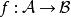 仿射變換
仿射變換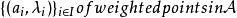 仿射變換
仿射變換給定同一場中的兩個仿射空間
與,一函式為一仿射映射若且唯若對任一加權點的集合我們得到
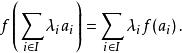 仿射變換
仿射變換此定義等價於 f 保留了質心。
表示
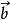 仿射變換
仿射變換如上所示,仿射變換為兩函式的複合:平移及線性映射。普通向量代數用矩陣乘法呈現線性映射,用向量加法表示平移。正式言之,於有限維度之例中,假如該線性映射被表示為一矩陣“A”,平移被表示為向量,一仿射映射f可被表示為
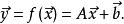 仿射變換
仿射變換增廣矩陣
使用一增廣矩陣與一增廣向量, 用一矩陣乘法同時表示平移與線性映射是有可能的。此技術需要所有向量在其末端擴長 “1”且所有矩陣都於底部添加一排零,右邊擴長一列轉換向量,及右下角添加一個 “1”。
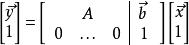 仿射變換
仿射變換等價於
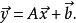 仿射變換
仿射變換以上所言之擴長矩陣被稱為 “仿射變換矩陣”,又或稱為 “投射變換矩陣” (其可套用於投影轉換).
此表示法以 K之半直積與 GL( n, k)展示了 所有可逆仿射變換的集合。 此為一個於眾函式集結下進行的一個群,被稱為仿射群。
普通矩陣向量乘法總將原點映射至原點,因此無法呈現平移(原點必須映射至其他點)。藉由於所有向量上擴增一坐標 “1”,我們將原空間映至更高維空間的一個子集合以進行變換。在該空間中,原本之空間占有了擴長坐標一的1的子集合。 因此原空間的原點可在(0,0, ... 0, 1). 原空間的平移可藉由更高維度空間的線性轉換來達成(即為錯切變換)。在高維度中的坐標即為齊次坐標的一例。 假如原空間為歐幾里德, 則更高維空間為實射影空間.
使用齊次坐標的優點為,藉由相對應矩陣之乘積,可將任意數目的仿射變換結合為一。此性質被大量運用於計算機圖形,計算機視覺與機器人學。
性質
一仿射變換保留了:
(1)點之間的共線性,例如通過同一線之點 (即稱為共線點)在變換後仍呈共線。
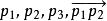 仿射變換
仿射變換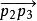 仿射變換
仿射變換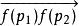 仿射變換
仿射變換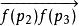 仿射變換
仿射變換(2)向量沿著一線的比例,例如對相異共線三點與的比例同於及。
(3)帶不同質量的點之質心。
一仿射變換為可逆的若且唯若A為可逆的。在矩陣表示中,其逆元為
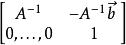 仿射變換
仿射變換可逆仿射變換組成仿射群,其中包含具n階的一般線性群為子群,且自身亦為一n+1階的一般線性群之子群。 當A為常數乘以正交矩陣時,此子集合構成一子群,稱之為相似變換。舉例而言,假如仿射變換於一平面上且假如A之行列式為1或-1,那么該變換即為等面積變換。此類變換組成一稱為等仿射群的子集。一同時為等面積變換與相似變換之變換,即為一平面上保持歐幾里德距離不變之保距映射。 這些群都有一保留了原定向的子群,也就是其對應之 A的行列式大於零。在最後一例中,即為三維中剛體運動之群(鏇轉加平移)。 假如有一不動點,我們可以將其當成原點,則仿射變換被縮還到一線性變換。這使得變換更易於分類與理解。舉例而言,將一變換敘述為特定軸的鏇轉,相較於將其形容為平移與鏇轉的結合,更能提供變換行為清楚的解釋。只是,這取決於套用與內容。
實例
實數
函式 f: R→ R, f( x) = mx+ c,其中 m與 c為常數,此即為一般之仿射變換。
有限域
以下等式表示了有限域(2)中的仿射變換:
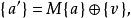 仿射變換
仿射變換此處[M]為矩陣 且 {v} 為向量:
此處 [M] 為矩陣且 {v} 為向量  仿射變換 仿射變換 |
舉例來講,將以大端序二進制表示的元素{a} = y+ y+ y+ y= {11001010}轉換成大端序十六進制,計算如下:
 仿射變換
仿射變換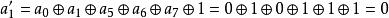 仿射變換
仿射變換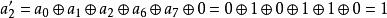 仿射變換
仿射變換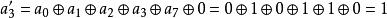 仿射變換
仿射變換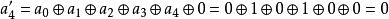 仿射變換
仿射變換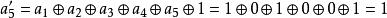 仿射變換
仿射變換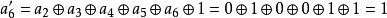 仿射變換
仿射變換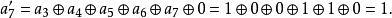 仿射變換
仿射變換於是, {a′} = y7 + y6 + y5 + y3 + y2 + 1 = {11101101} = {ED}。
平面幾何
在 ℝ,左方所示之變換即為以下映射:
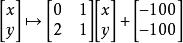 仿射變換
仿射變換將原紅色三角形之三個頂點作變換後給出了新藍色三角形的三個頂點。事實上,所有三角形皆可由仿射變換來達成,所有平行四邊形也可以,但一般四邊形不行。