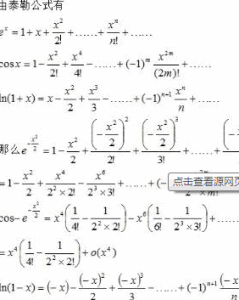簡介
數學中, 泰勒公式是一個用 函式在某 點的信息描述其附近取值的 公式。如果函式足夠 光滑的話,在已知函式在某一點的各階 導數值的情況之下,泰勒公式可以用這些導數值的相應倍數作為 係數構建一個 多項式來近似函式在這一點的 鄰域中的值。帶拉格朗日餘項的泰勒公式還給出了這個多項式和實際的函式值之間的偏差。泰勒公式得名於 英國數學家布魯克·泰勒。他在1712年的一封信里首次敘述了這個公式,儘管1671年詹姆斯·格雷高里已經發現了它的特例。公式定義
泰勒公式(Taylor's formula)
形式1:帶Peano餘項的Taylor公式:
若f(x)在x0處有n階導數,則存在x0的一個鄰域(x0-δ,x0+δ)內任意一點x(δ>0),成立下式:
f(x)=f(x0)+f'(x0)/1!*(x-x0)+f''(x0)/2!*(x-x0)^2+…+f(n) (x0)/n!(x-x0)^n+o((x-x0)^n)
f(n)(x)表示f(x)的n階導數,f(n) (x0)表示f(n)(x)在x0處的取值
(可以反覆使用L'Hospital法則來推導)
形式2::帶Lagrange餘項的Taylor公式:
若 函式f(x)在閉區間[a,b]上有n階連續 導數,在(a,b)上有n+1階導數。任取x0∈[a,b]是一定點,則對任意x∈[a,b]成立下式:
f(x)=f(x。)+f'(x。)(x-x。)+f''(x。)/2!*(x-x。)^2,+f'''(x。)/3!*(x-x。)^3+……+f(n)(x。)/n!*(x-x。)^n+Rn(x),
Rn(x)=f(n+1)(ξ)/(n+1)!*(x-x。)^(n+1), ξ在x。和x之間,是依賴於x的量。
(註:f(n)(x。)是f(x。)的n階導數,不是f(n)與x。的相乘。)
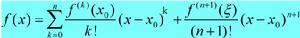
函式的 Maclaurin展開指上面Taylor公式中x0取0的情況,即是Taylor公式的特殊形式,反過來通過平移和換元, Maclaurin展開式和上面的展開式是等價的。
Taylor公式最典型的套用就是求任意函式的近似值。Taylor公式還可以求等價無窮小,證明不等式,求極限等
證明
我們知道f(x)=f(x.)+f'(x.)(x-x.)+α(根據 拉格朗日中值定理導出的有限增量定理有limΔx→0 f(x.+Δx)-f(x.)=f'(x.)Δx,其中誤差α是在limΔx→0 即limx→x.的前提下才趨向於0,所以在近似計算中往往不夠精確;於是我們需要一個能夠足夠精確的且能估計出誤差的多項式:
P(x)=A0+A1(x-x.)+A2(x-x.)^2+……+An(x-x.)^n
來近似地表示函式f(x)且要寫出其誤差f(x)-P(x)的具體表達式。設函式P(x)滿足P(x.)=f(x.),P'(x.)=f'(x.),P''(x.)=f''(x.),……,P(n)(x.)=f(n)(x.),於是可以依次求出A0、A1、A2、……、An。顯然,P(x.)=A0,所以A0=f(x.);P'(x.)=A1,A1=f'(x.);P''(x.)=2!A2,A2=f''(x.)/2!……P(n)(x.)=n!An,An=f(n)(x.)/n!。至此,多項的各項係數都已求出,得:P(x)=f(x.)+f'(x.)(x-x.)+[f''(x.)/2!](x-x.)^2+……+[f(n)(x.)/n!](x-x.)^n.
接下來就要求誤差的具體表達式了。設Rn(x)=f(x)-P(x),於是有Rn(x.)=f(x.)-P(x.)=0。所以可以得出Rn(x.)=Rn'(x.)=Rn''(x.)=……=Rn(n)(x.)=0。根據 柯西中值定理可得Rn(x)/(x-x.)^(n+1)=(Rn(x)-Rn(x.))/((x-x.)^(n+1)-0)=Rn'(ξ1)/(n+1)(ξ1-x.)^n(註:(x.-x.)^(n+1)=0),這裡ξ1在x和x.之間;繼續使用柯西中值定理得(Rn'(ξ1)-Rn'(x.))/((n+1)(ξ1-x.)^n-0)=Rn''(ξ2)/n(n+1)(ξ2-x.)^(n-1)這裡ξ2在ξ1與x.之間;連續使用n+1次後得出Rn(x)/(x-x.)^(n+1)=Rn(n+1)(ξ)/(n+1)!,這裡ξ在x.和x之間。但Rn(n+1)(x)=f(n+1)(x)-P(n+1)(x),由於P(n)(x)=n!An,n!An是一個常數,故P(n+1)(x)=0,於是得Rn(n+1)(x)=f(n+1)(x)。綜上可得,餘項Rn(x)=f(n+1)(ξ)/(n+1)!?(x-x.)^(n+1)。一般來說展開函式時都是為了計算的需要,故x往往要取一個定值,此時也可把Rn(x)寫為Rn。
麥克勞林展開式
函式的 Maclaurin展開指上面Taylor公式中x0取0的情況,即是Taylor公式的特殊形式.
Taylor公式的套用
:
1、展開三角函式y=sinx和y=cosx。
解:根據導數表得:f(x)=sinx,f'(x)=cosx,f''(x)=-sinx,f'''(x)=-cosx,f⑷(x)=sinx……
f(n)(x)=sin(x+nπ/2)
於是得出了 周期規律。分別算出f(0)=0,f'(0)=1,f''(x)=0,f'''(0)=-1,f⑷=0……
最後可得:sinx=x-x^3/3!+x^5/5!-x^7/7!+x^9/9!+Rn(x)
Rn(x)=o(x^10) (Peano餘項)
或Rn(x)=sin(ξ+11π/2)/11!*x^11,ξ∈(0,x)
類似地,可以展開y=cosx。
2、計算近似值e=lim x→∞ (1+1/x)^x。
解:對指數函式y=e^x運用 麥克勞林展開式並捨棄餘項:
e^x≈1+x+x^2/2!+x^3/3!+……+x^n/n!
當x=1時,e≈1+1+1/2!+1/3!+……+1/n!
取n=10,即可算出近似值e≈2.7182818。
3、歐拉公式:e^ix=cosx+isinx(i為-1的開方,即一個虛數單位)
證明:這個公式把 複數寫為了冪指數形式,其實它也是由 麥克勞林展開式確切地說是麥克勞林級數證明的。過程具體不寫了,就把思路講一下:先展開指數函式e^z,然後把各項中的z寫成ix。由於i的冪 周期性,可已把係數中含有土i的項用乘法分配律寫在一起,剩餘的項寫在一起,剛好是cosx,sinx的展開式。然後讓sinx乘上提出的i,即可導出 歐拉公式。有興趣的話可自行證明一下。
背景
e的來源和作用
e的發現始於微分,當 h 逐漸接近零時,計算 之值,其結果無限接近一定值 2.71828...,這個定值就是 e,最早發現此值的人是 瑞士著名數學家 歐拉,他以自己姓名的字頭小寫 e 來命名此無理數.
計算對數函式 的導數,得,當 a=e 時,的導數為,因而有理由使用以 e 為底的對數,這叫作自然對數.
若將指數函式 ex 作泰勒展開,則得
以 x=1 代入上式得
此級數收斂迅速,e 近似到小數點後 40 位的數值是
將指數函式 ex 擴大它的定義域到 複數 z=x+yi 時,由
透過這個級數的計算,可得
由此,De Moivre 定理,三角函式的和差角公式等等都可以輕易地導出.譬如說,z1=x1+y1i,z2=x2+y2i,
另方面,
所以,
我們不僅可以證明 e 是無理數,而且它還是個超越數,即它不是任何一個整係數多項式的根,這個結果是 Hermite 在1873年得到的.
甲)差分.
考慮一個離散函式(即數列) R,它在 n 所取的值 u(n) 記成 un,通常我們就把這個函式書成 或 (un).數列 u 的差分 還是一個數列,它在 n 所取的值以定義為
以後我們乾脆就把 簡記為
(例):數列 1,4,8,7,6,-2,... 的差分數列為 3,4,-1,-1,-8 ...
註:我們說「數列」是「定義在離散點上的函式」如果在高中,這樣的說法就很惡劣.但在此地,卻很恰當,因為這樣才跟連續型的函式具有完全平行的類推.
差分運算元的性質
(i) [合稱線性]
(ii) (常數) [差分方程根本定理]
(iii)
其中,而 (n(k) 叫做排列數列.
(iv) 叫做自然等比數列.
(iv)' 一般的指數數列(幾何數列)rn 之差分數列(即「導函式」)為 rn(r-1)
(乙).和分
給一個數列 (un).和分的問題就是要算和 . 怎么算呢 我們有下面重要的結果:
定理1 (差和分根本定理) 如果我們能夠找到一個數列 (vn),使得,則
和分也具有線性的性質:
甲)微分
給一個函式 f,若 牛頓商(或差分商) 的極限 存在,則我們就稱此極限值為 f 為點 x0 的導數,記為 f'(x0) 或 Df(x),亦即
若 f 在定義區域上每一點導數都存在,則稱 f 為可導微函式.我們稱 為 f 的導函式,而 叫做微分運算元.
微分運算元的性質:
(i) [合稱線性]
(ii) (常數) [差分方程根本定理]
(iii) Dxn=nxn-1
(iv) Dex=ex
(iv)' 一般的指數數列 ax 之導函式為
(乙)積分.
設 f 為定義在 [a,b] 上的函式,積分的問題就是要算陰影的面積.我們的辦法是對 [a,b] 作分割:
;其次對每一小段 [xi-1,xi] 取一個樣本點 ;再求近似和 ;最後再取極限 (讓每一小段的長度都趨近於 0).
若這個極限值存在,我們就記為 的幾何意義就是陰影的面積.
(事實上,連續性也「差不多」是積分存在的必要條件.)
積分運算元也具有線性的性質:
定理2 若 f 為一連續函式,則 存在.(事實上,連續性也「差不多」是積分存在的必要條件.)
定理3 ( 微積分根本定理) 設 f 為定義在閉區間 [a,b] 上的連續函式,我們欲求積分 如果我們可以找到另一個函式 g,使得 g'=f,則
註:⑴⑵兩式雖是類推,但有一點點差異,即和分的上限要很小心!
上面定理1及定理3基本上都表述著差分與和分,微分與積分,是兩個互逆的操作,就好像加法與減法,乘法與除法是互逆的操作一樣.
我們都知道差分與微分的操作比和分與積分簡單多了,而上面定理1及定理3告訴我們,要計算 (un) 的和分及 f 的積分,只要去找另一個 (vn) 及 g 滿足,g'=f (這是差分及微分的問題),那么對 vn 及 g 代入上下限就得到答案了.換句話說,我們可以用較簡單的差分及微分操作來掌握較難的和分及積分操作,這就是"以簡御繁"的精神.牛頓與萊布尼慈對微積分最大的貢獻就在此.
甲)Taylor展開公式
這分別有離散與連續的類推.它是數學中「逼近」這個重要想法的一個特例.逼近想法的意思是這樣的:給一個函式 f,我們要研究 f 的行為,但 f 本身可能很複雜而不易對付,於是我們就想法子去找一個較「簡單」的函式 g,使其跟 f 很「靠近」,那么我們就用 g 來取代 f.這又是以簡御繁的精神表現.由上述我們看出,要使用逼近想法,我們還需要澄清
兩個問題:即如何選取簡單函式及逼近的尺度.
(一) 對於連續世界的情形,Taylor 展式的逼近想法是選取多項函式作為簡單函式,並且用局部的「切近」作為逼近尺度.說得更明白一點,給一個直到到 n 階都可導微的函式 f,我們要找一個 n 次多項函式 g,使其跟 f 在點 x0 具有 n 階的「切近」,即,答案就是
此式就叫做 f 在點 x0 的 n 階 Taylor 展式.
g 在 x0 點附近跟 f 很靠近,於是我們就用 g 局部地來取代 f.從而用 g 來求得 f 的一些局部的定性行為.因此 Taylor 展式只是局部的逼近.當f是足夠好的一個函式,即是所謂解析的函式時,則 f可展成 Taylor 級數,而且這個 Taylor 級數就等於 f 自身.
值得注意的是,一階 Taylor 展式的特殊情形,此時 g(x)=f(x0)+f'(x0)(x-x0) 的圖形正好是一條通過點 (x0,f(x0)) 而且切於 f 的圖形之直線.因此 f 在點 x0 的一階 Taylor 展式的意義就是,我們用過點 (x0,f(x0)) 的切線局部地來取代原來 f 曲線.這種局部化「用平直取代彎曲」的精神,是微分學的精義所在.
利用 Taylor 展式,可以幫忙我們做很多事情,比如判別函式的極大值與極小值,求積分的近似值,作函式表(如三角函式表,對數表等),這些都是意料中事.事實上,我們可以用逼近的想法將微積分「一以貫之」.
複次我們注意到,我們選取多項函式作為逼近的簡單函式,理由很簡單:在眾多初等函式中,如三角函式,指數函式,對數函式,多項函式等,從算術的觀點來看,以多項函式最為簡單,因為要計算多項函式的值,只牽涉到加減乘除四則運算,其它函式就沒有這么簡單.
當然,從別的解析觀點來看,在某些情形下還另有更有用更重要的簡單函式.例如,三角多項式,再配合上某種逼近尺度,我們就得到 Fourier 級數展開,這在 套用數學上占有舉足輕重的地位.(事實上,Fourier 級數展開是採用最小方差的逼近尺度,這在 高等數學中經常出現,而且在統計學中也有套用.)
註:取 x0=0 的特例,此時 Taylor 展式又叫做 Maclaurin 展式.不過只要會做特例的展開,欲求一般的 Taylor 展式,作一下平移(或變數代換)就好了.因此我們大可從頭就只對 x=0 點作 Taylor 展式.
(二) 對於離散的情形,Taylor 展開就是:
給一個數列,我們要找一個 n 次多項式數列 (gt),使得 gt 與 ft 在 t=0 點具有 n 階的「差近」.所謂在 0 點具有 n 階差近是指:
答案是 此式就是離散情形的 Maclaurin 公式.
乙)分部 積分公式與Abel分部和分公式的類推
(一) 分部 積分公式:
設 u(x),v(x) 在 [a,b] 上連續,則
(二) Abel分部和分公式:
設(un),(v)為兩個數列,令 sn=u1+......+un,則
上面兩個公式分別是萊布尼慈導微公式 D(uv)=(Du)v+u(Dv),及萊布尼慈差分公式 的結論.注意到,這兩個萊布尼慈公式,一個很對稱,另一個則不然.
(丁)複利與連續複利 (這也分別是離散與連續之間的類推)
(一) 複利的問題是這樣的:有本金 y0,年利率 r,每年複利一次,要問 n 年後的本利和 yn= 顯然這個數列滿足差分方程 yn+1=yn(1+r)
根據(丙)之(二)得知 yn=y0(1+r)n 這就是複利的公式.
(二) 若考慮每年複利 m 次,則 t 年後的本利和應為
令,就得到連續複利的概念,此時本利和為y(t)=y0ert
換句話說,連續複利時,t 時刻的本利和 y(t)=y0ert 就是 微分方程 y'=ry 的解答.
由上述我們看出離散複利問題由差分方程來描述,而連續複利的問題由微分方程來描述.對於常係數線性的差分方程及微分方程,解方程式的整個要點就是疊合原理,因此求解的辦法具有完全平行的類推.
(戊)Fubini 重和分定理與 Fubini 重積分定理(也是離散與連續之間的類推)
(一) Fubini 重和分定理:給一個兩重指標的數列 (ars),我們要從 r=1 到 m,s=1到 n,對 (ars) 作和,則這個和可以這樣求得:光對 r 作和再對 s 作和(反過來亦然).亦即我們有
(二)Fubini 重積分定理:設 f(x,y) 為定義在 上之可積分函式,則
當然,變數再多幾個也都一樣.
(己)Lebesgue 積分的概念
(一) 離散的情形:給一個數列 (an),我們要估計和,Lebesgue 的想法是,不管這堆數據指標的順序,我們只按數值的大小來分堆,相同的分在一堆,再從每一堆中取一個數值,乘以該堆的個數,整個作和起來,這就得到總和.
(二)連續的情形:給一個函式 f,我們要定義曲線 y=f(x) 跟 X 軸從 a 到 b 所圍出來的面積.
Lebesgue 的想法是對 f 的影域 作分割:
函式值介 yi-1 到 yi 之間的 x 收集在一齊,令其為,於是 [a,b] 就相應分割成,取樣本點,作近似和
讓影域的分割加細,上述近似和的極限若存在的話,就叫做 f 在 [a,b] 上的 Lebesgue 積分.
餘項
泰勒公式的餘項f(x)=f(a) + f'(a)(x-a)/1! + f''(a)(x-a)^2/2! + …… + f(n)(a)(x-a)^n/n! + Rn(x) [其中f(n)是f的n階導數]
泰勒餘項可以寫成以下幾種不同的形式:
⒈佩 亞諾(Peano)餘項:
Rn(x) = o((x-a)^n)
⒉施勒米爾希-羅什(Schlomilch-Roche)餘項:
Rn(x) = f(n+1)(a+θ(x-a))(1-θ)^(n+1-p)(x-a)^(n+1)/(n!p)
[f(n+1)是f的n+1階導數,θ∈(0,1)]
⒊拉格朗日(Lagrange)餘項:
Rn(x) = f(n+1)(a+θ(x-a))(x-a)^(n+1)/(n+1)!
[f(n+1)是f的n+1階導數,θ∈(0,1)]
⒋柯西(Cauchy)餘項:
Rn(x) = f(n+1)(a+θ(x-a))(1-θ)^n (x-a)^(n+1)/n!
[f(n+1)是f的n+1階導數,θ∈(0,1)]
⒌積分餘項:
Rn(x) = [f(n+1)(t)(x-t)^n在a到x上的積分]/n!
[f(n+1)是f的n+1階導數]
這裡諸多餘項事實上很多是等價的。
泰勒簡介
18世紀早期 英國牛頓學派最優秀代表人物之一的英國數學家泰勒(Brook Taylor), 於1685 年8月18日在英格蘭 德爾塞克斯郡的 埃德蒙頓市出生。1701年,泰勒進 劍橋大學的聖約翰學院學習。1709年後移居 倫敦,獲得法學學士學位。1712年當選為 英國皇家學會會員,同年進入促裁牛頓和萊布尼茲發明微積分優先權爭論的委員會。並於兩年後獲法學博士學位。從1714年起擔任皇家學會第一秘書,1718年以健康為由辭去這一職務。1717年,他以泰勒定理求解了數值方程。最後在1731年1 2月29日於 倫敦逝世。
由於工作及健康上的原因,泰勒曾幾次訪問 法國並和法國數學家蒙莫爾多次通信討論級數問題和機率論的問題。1708年,23歲的泰勒得到了“振動中心問題”的解,引起了人們的注意,在這個工作中他用了 牛頓的瞬的記號。 從1714到1719年,是泰勒在數學上多產的時期。
主要著作
他的兩本著作:《正和反的增量法》及《直線透視》都出版於1715年,它們的第二版分別出於1717和1719年。從1712到1724年,他在《哲學會報》上共發表了13篇文章,其中有些是通信和評論。文章中還包含毛細管現象、磁學及溫度計的實驗記錄。
在生命的後期,泰勒轉向宗教和哲學的寫作,他的第三本著作《哲學的沉思》在他死後由外孫W.楊於1793年出版。
泰勒以微積分學中將 函式展開成無窮 級數的定理著稱於世。這條定理大致可以敘述為:函式在一個點的鄰域內的值可以用函式在該點的值及各階 導數值組成的無窮級數表示出來。然而,在半個世紀裡,數學家們並沒有認識到泰勒定理的重大價值。這一重大價值是後來由 拉格朗日發現的,他把這一定理刻畫為微積分的基本定理。泰勒定理的嚴格證明是在定理誕生一個世紀之後,由柯西給出的。
泰勒定理開創了有限差分理論,使任何單變數函式都可展成 冪級數;同時亦使 泰勒成了有限差分理論的奠基者。泰勒於書中還討論了 微積分對一系列物理 問題之套用,其中以有關弦的橫向振動之結果尤為重要。他透過求解方程 導出了基本頻率公式,開創了研究弦振問題之先河。此外,此書還包括了他於 數學上之其他創造性工作,如論述常 微分方程的奇異解,曲率 問題之研究等。
1715年,他出版了另一名著《線性透 視論》,更發表了再版的《線性透視原理》(1719)。他以極嚴密之形式展開其線性透 視學體系,其中最突出之貢獻是提出和使用「沒影點」概念, 這對攝影測量製圖學之發展有 一定影響。另外,還撰有哲學遺作,發表於1793年。
展開式
泰勒公式可以用(無限或者有限)若干項連加式(-級數)來表示一個函式,這些相加的項由函式在某一點(或者加上在臨近的一個點的次導數)的導數求得。
對於正整數n,若函式在閉區間上階連續可導,且在上階可導。任取是一定點,則對任意成立下式:
其中,表示的n階導數,多項式稱為函式在a處的泰勒展開式,剩餘的是泰勒公式的餘項,是的高階無窮小。[1]
餘項
泰勒公式的餘項可以寫成以下幾種不同的形式:
1、佩亞諾(Peano)餘項:
這裡只需要n階導數存在
2、施勒米爾希-羅什(Schlomilch-Roche)餘項:
其中θ∈(0,1)。
3、拉格朗日(Lagrange)餘項:
其中θ∈(0,1)。
4、柯西(Cauchy)餘項:
其中θ∈(0,1)。
5、積分餘項:
以上諸多餘項事實上很多是等價的。
2公式推廣
編輯
麥克勞林展開
函式的麥克勞林展開指上面泰勒公式中a取0的情況,即是泰勒公式的特殊形式,若在x=0處n階連續可導,則下式成立:
其中表示的n階導數。[1]
泰勒中值定理
若在包含的某開區間(a,b)內具有直到n+1階的導數,則當x∈(a,b)時,有
其中是n階泰勒公式的拉格朗日餘項:
,
多元泰勒公式
對於多元函式,也有類似的泰勒公式。設B(a,r)是歐幾里得空間RN中的開球,ƒ是定義在B(a,r)的閉包上的實值函式,並在每一點都存在所有的n+1次偏導數。這時的泰勒公式為:
對所有
3驗證推導
編輯
我們知道,根據拉格朗日中值定理導出的有限增量定理有:
於是:
其中誤差α是在limΔx→0即limx→x0的前提下才趨向於0,所以在近似計算中往往不夠精確;於是我們需要一個能夠足夠精確的且能估計出誤差的多項式:
來近似地表示函式f(x)且要寫出其誤差f(x)-P(x)的具體表達式。設函式P(x)滿足:
於是可以依次求出A0、A1、A2、……、An,顯然有:
,所以;
,所以;
,所以;
,所以;
至此,多項的各項係數都已求出,得:
以上就是函式的泰勒展開式。[1]
接下來就要求誤差的具體表達式了。設,令得到:
進而:
根據柯西中值定理:
其中;
繼續使用柯西中值定理得到:
其中;
連續使用n+1次後得到:
其中;
同時:
而:
進而:
綜上可得:
一般來說展開函式時都是為了計算的需要,故x往往要取一個定值,此時也可把Rn(x)寫為Rn。[1]
4發展簡史
編輯
希臘哲學家芝諾在考慮利用無窮級數求和來得到有限結果的問題時,得出不可能的結論-芝諾悖論,這些悖論中最著名的兩個是“阿喀琉斯追烏龜”和“飛矢不動”。
後來,亞里士多德對芝諾悖論在哲學上進行了反駁,直到德謨克利特以及後來的阿基米德進行研究,此部分數學內容才得到解決。阿基米德套用窮舉法使得一個無窮級數能夠被逐步的細分,得到了有限的結果。[2]
14世紀,瑪達瓦發現了一些特殊函式,包括正弦、餘弦、正切、反正切等三角函式的泰勒級數。
17世紀,詹姆斯·格雷果里同樣繼續著這方面的研究,並且發表了若干麥克勞林級數。直到1712年,英國牛頓學派最優秀代表人物之一的數學家泰勒提出了一個通用的方法,這就是為人們所熟知的泰勒級數;愛丁堡大學的科林·麥克勞林教授發現了泰勒級數的特例,稱為麥克勞林級數。
5公式套用
編輯
實際套用中,泰勒公式需要截斷,只取有限項,一個函式的有限項的泰勒級數叫做泰勒展開式。泰勒公式的餘項可以用於估算這種近似的誤差。
泰勒展開式的重要性體現在以下三個方面:
冪級數的求導和積分可以逐項進行,因此求和函式相對比較容易。
一個解析函式可被延伸為一個定義在複平面上的一個開片上的解析函式,並使得複分析這種手法可行。
泰勒級數可以用來近似計算函式的值。
實例
1、展開三角函式和。
解:根據導數表得:
最後可得:
其中為皮亞諾餘項:
或:
其中
[3]類似地,可以展開y=cos(x)。
2、計算近似值
解:對指數函式
運用麥克勞林展開式並捨棄餘項:
當x=1時:
取n=10,即可算出近似值e≈2.7182818。[3]
3、歐拉公式:
(其中,即一個虛數單位)
證明:這個公式把複數寫為了冪指數形式,其實它也是由麥克勞林展開式確切地說是麥克勞林級數證明的。證明思路是先展開指數函式e^z,然後把各項中的z寫成ix。由於i的冪周期性,可已把係數中含有土i的項用乘法分配律寫在一起,剩餘的項寫在一起,剛好是cosx,sinx的展開式。然後讓sinx乘上提出的i,即可導出歐拉公式。