概念
 柯西中值定理
柯西中值定理柯西(Cauchy)中值定理設函式f(x),g(x)滿足
⑴在閉區間[a,b]上連續;
⑵在開區間(a,b)內可導;
⑶對任一x∈(a,b)有g'(x)≠0,
則存在ξ∈(a,b),使得
[f(b)-f(a)]/[g(b)-g(a)]=f'(ξ)/g'(ξ)
證明
 柯西中值定理
柯西中值定理由羅爾中值定理知:存在ξ∈(a,b),使得F'(ξ)=0.
故F'(ξ)=f'(ξ)-[f(a)-f(b)]g'(ξ)/[g(a)-g(b)]=0,即f'(ξ)/g'(ξ)=[f(a)-f(b)]/[g(a)-g(b)]
命題得證。
拉氏定理
在柯西中值定理中,若取g(x)=x時,則其結論形式和拉格朗日中值定理的結論形式相同。
因此,拉格朗日中值定理為柯西中值定理的一個特例;反之,柯西中值定理可看作是拉格朗日中值定理的推廣。幾何意義
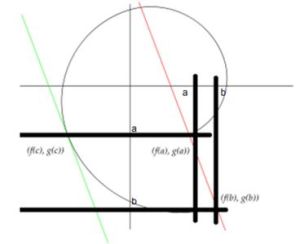
若令u=f(x),v=g(x),這個形式可理解為參數方程,而[f(a)-f(b)]/[g(a)-g(b)]則是連線參數曲線的端點斜率,f'(ξ)/g'(ξ)表示曲線上某點處的切線斜率,在定理的條件下,可理解如下:
用參數方程表示的曲線上至少有一點,它的切線平行於兩端點所在的弦。套用
判斷函式的單調性
函式的單調性也就是函式的增減性,怎樣才能判斷函式的增減性呢?
我們知道若函式在某區間上單調增(或減),則在此區間內函式圖形上切線的斜率均為正(或負),也就是函式的導數在此區間上均取正值(或負值).因此我們可通過判定函式導數的正負來判定函式的增減性.例1 設f(0)=0,f(x)在(0,+∞)上單調遞增.證明:f(x)x在(0,+∞)上單調遞增.
證明由柯西中值定理,可以得出f(x)x=f(x)-f(0)x-0=f′(ξ)1=f′(ξ),0<;ξ 0.這樣就可以證明f(x)x在(0,+∞)上單調遞增.
不等式極限
柯西中值定理的一個極其重要的套用就是可以用來計算未定型的極限.兩個無窮小量或兩個無窮大量的比的極限統稱為不定式極限,分別記00,∞∞,0/∞;0-∞,∞-∞和∞∞型不定式.仔細觀察柯西中值定理表達式的形式,可以看到兩個函式式的比值,在移動條件下可以化成兩個函式的導數的比值,這樣就有可能使得作為未定型的分式的分子與分母所表示的函式,我們將以微分中值定理為理論依據,通過求導,建立一個簡便而有效的求非未定型極限的方法.我們得出下面這個定理:
⑴兩個函式f(x)和g(x)在開區間(a,b)可微,並且在這個開區間上,g(x)的導數不等於0;
⑵存在極限limx→a+0f′(x)g′(x)=A,其中A為一個有限的常數.則在以下情況下:limx→a+0f(x)=0和limx→a+0g(x)=0或者limx→a+0g(x)=∞.那么就有:limx→a+0f(x)g(x)=limx→a+0f′(x)g′(x)=A.反過來在區間的另一個端點也存在相類似的結果.這個定理就稱之為羅必達法則,能有效地套用於未定型的極限計算.
羅必達法則可以運用於7種未定型的極限計算,而最為基本的未定型只有兩種:00和∞∞.00和∞∞型的我們都知道,那么在此就不做介紹了.其他的未定型都可以化成這兩種形式:
①0;∞型.
通過恆等式:f(x)·g(x)=f(x)1g(x),從而得到00或∞∞這兩種基本形式.
②∞-∞型.
通過恆等式:f(x)-g(x)=1g(x)-1f(x)1f(x)×1g(x),從而得到00型.
③00,∞0,1∞型.
通過恆等式f(x)g(x)=elnf(x)g(x)=eg(x)lnf(x),從而得到00;0-∞,∞-∞,00,∞0,1∞型.再進一步化成00或∞∞這兩種基本形式.
對於兩種基本形式的未定型,直接套用洛必達法則即可,即表示為limf(x)g(x)=limf′(x)g′(x)=A.
顯然這時的條件為f′(x),g′(x)都存在,並且g′(x)≠0.還有一個不是很明顯,因此初學者常常犯錯誤的地方,就是要求f(x)和g(x)同時以0或者∞為極限.在實際做題時,一定要注意隨時驗證這三個條件,否則必定會犯錯誤..
例2 證明:limx→0+x1-ex=-1.
證明令t=x,當x→0+時有t→0+,則可以得到:
limx→0+x1-ex=limx→0+t1-et=limx→0+1-et=-1.
推導中值公式
例3 設f(x)在開區間(a,b)內二次可微,證明:任意的x,x0∈(a,b),存在ξ∈(x,x0),使f(x)=f(x0)+f′(x0)(x-x0)+12f″(ξ)(x-x0)2成立(這就是泰勒公式一次展開式).證明由題可知,只需證明x>x0這一種情況.令
F(x)=f(x)-f(x0)-f′(x0)(x-x0),G(x)=12(x-x0)2.
求導可得F′(x)=f′(x)-f′(x0),G′(x)=x-x0.
因為F(x0)=G(x0)=0,F′(x0)=G′(x0)=0兩次套用到柯西中值定理,可以得到:
f(x)-f(x0)-f(x0)(x-x0)12(x-x0)2=F(x)G(x)=F(x)-F(x0)G(x)-G(x0)=F′(η)G′(η)=F′(η)-F′(x0)G′(η)-G′(x0)=F″(ξ)G″(ξ)=F″(ξ).
其中η∈(x,x0),ξ∈(x0,η),則f(x)=f(x0)+f′(x0)(x-x0)+12f″(ξ)(x-x0)2得到證明.故命題得證.
研究函式的某些特性
⑴證明中值點的存在性例4 設函式f在區間[a,b]上連續,在(a,b)內可導,則?ξ∈(a,b),使得f(b)-f(a)=ξlnbaf′(ξ).
證明設g(x)=lnx,顯然它在[a,b]上與f一起滿足柯西中值定理的條件,於是存在ξ∈(a,b),使得f(b)-f(a)lnb-lna=f′(ξ)1ξ,即存在ξ∈(a,b)使得f(b)-f(a)=ξf′(ξ)lnba.
⑵證明恆等式
例5 證明:arcsinx+arccosx=π2,x∈[0,1].
證明令f(x)=arcsinx+arccosx,則f′(x)=11-x2-11-x2≡0,?x∈(0,1),由於f(x)在[0,1]連續,所以f(x)≡f(0)=π2.

