定義
在隨機事件的大量重複出現中,往往呈現幾乎必然的規律,這個規律就是大數定律。通俗地說,這個定理就是,在試驗不變的條件下,重複試驗多次,隨機事件的頻率近似於它的機率。比如,我們向上拋一枚硬幣,硬幣落下後哪一面朝上本來是偶然的,但當我們上拋硬幣的次數足夠多後,達到上萬次甚至幾十萬幾百萬次以後,我們就會發現,硬幣每一面向上的次數約占總次數的二分之一。偶然中包含著某種必然。
大數定律分為弱大數定律和強大數定律。
發展歷史
 大數定理
大數定理表現形式
初等機率
(1)帶方差的弱大數定律:若小於無窮,則依機率收斂到0。
證明方法:Chebyshev不等式即可得到。這個證明是Chebyshev給出的。
(2)帶均值的弱大數定律:若u存在,則依機率收斂到0。
證明方法:用Taylor展開特徵函式,證明其收斂到常數,得到依分布收斂,然後再用依分布收斂到常數等價於依機率收斂。
現代機率
(3).精確弱大數定律:若xP(|X|>x)當x趨於無窮時收斂到0,則依機率收斂到0,其中un=E[X1_{|X|<n}].(在這個定理里,不需要u存在。)
證明方法:需要用到截斷隨機變數X1{|X|<n}.然後要用的三角陣列的依機率收斂定理和Fubini定理分析積分變換。
(4).帶4階矩的強大數定律:若E(X^4)小於無窮,則幾乎必然收斂到0.
證明方法:與(1)類似,先用Chebyshev不等式。然後因為4階矩的存在,得到P(S_n>nt)對任意常數t的收斂速度足夠快,滿足Borel-Cantelli的要求,用Borel-Cantelli引理得到大數定律。
(5).帶方差的強大數定律:若E(X^2)小於無窮,則幾乎必然收斂到0.
證明方法:用Kolgoromov三級數定理和Kronecker定理。
(6).精確強大數定律:若u存在,則幾乎必然收斂到0.
證明方法:這個大數定律的證明確實有幾種不同的方法。最早的證明是由數學大師Kolgoromov給出的。Durrett(2010)的書上用的是Etemadi(1981)的方法,需要截斷X,用到現代機率論的知識如Borel-Cantelli引理、Kolgomorov三級數定理、Fubini定理等。(感謝讀者指出,Durrett的書在倒向鞅一章中給出了大數定律的倒向鞅方法證明,只需要用到倒向鞅的知識和Hewitt-Savage0-1律,不過這也是現代機率論的知識。)
此外,還有很多不同的大數定律,不同分布的,不獨立的序列等。定律也不一定是關於隨機變數的,也可以是關於隨機函式的,甚至隨機集合的等等。以數學家命名的也有Khinchin大數定律(不獨立序列的強大數定律)、Chebyshev大數定律(弱大數定律(1))、Poisson大數定律(不同機率的隨機事件序列的大數定律)、Bernoulli大數定律(隨機事件的大數定律)、Kolgomorov大數定律(強大數定律(6))等等……
以上(1-6)是常見的獨立同分布序列的大數定律。其中,(3)和(6)是最嚴格也是最精妙的結果,證明所涉及的高等機率論知識也最多。它們成立的條件不僅是充分條件,也是必要條件,因此它們算是完結了大數定律的發展。大數定律的發展符合數學的一般規律:想證明某一結論,條件越弱(弱大數定律:2階矩條件->1階矩條件->沒矩條件;強大數定律:4階矩條件→2階矩條件→1階矩條件),證明也就變得越難。
雖然只有(3)和(6)是最精確的結果,但是必須認識到,數學的發展是一個循序漸進的過程,如果沒有前面那些更強條件下的定理,也無法得到最後的大數定律。
從最開始的自然界觀察到大數定律的存在,到最後證明最終形式,歷時數百年,現代機率論也在這個過程中建立起來。此外,雖然(3)和(6)比前面的(1)和(5)強很多,但是(1)和(5)的條件僅僅是2階矩(或方差)的存在,因此他們在幾百年間早就被廣泛使用,對於一般的社會科學問題、統計問題等已經足足夠用了。
總之,大數定律包含機率論里核心的知識。“大數定律的四種證法”儘管表述模糊,原意也充滿調侃,但並不是真如《孔乙己》里"回字四種寫法"所暗示的那樣迂腐或毫無價值。作為機率或統計專業的研究生,弄懂這些定理表述的區別和證明方法的區別和聯繫,了解前代數學家的工作,對於深刻理解現代機率論是很有好處的。當然,任何人也不應去死記硬背這些證法,只要能理解、弄清其中微妙即可。
舉例說明
 大數定律
大數定律幾乎處處收斂與依機率收斂不同。生活例子:開始上課了,慢慢地大家都安靜下來,這是幾乎處處收斂。絕大多數同學都安靜下來,但每一個人都在不同的時間不安靜,這是依機率收斂。
數學家
拉普拉斯
拉普拉斯,1749年3月23日生於法國西北部卡爾瓦多斯的博蒙昂諾日,曾任巴黎軍事學院數學教授,1795年任巴黎綜合工科學校教授,後又在高等師範學校任教授。1799年他還擔任過法國經度局局長,並在拿破崙政府中任過6個星期的內政部長,1816年被選為法蘭西學院院士,1817年任該院院長,1827年3月5日卒於巴黎。
拉普拉斯在研究天體問題的過程中,創造和發展了許多數學的方法,以他的名字命名的拉普拉斯變換、拉普拉斯定理和拉普拉斯方程,在科學技術的各個領域有著廣泛的套用。
德莫佛
德莫佛,法文原名AbrahamdeMoivre,(1667.05.26法國-1754.11.27英國倫敦),法國數學家。德莫佛對數學最著名的貢獻是德莫佛公式(deMoivreFormula)和德莫佛-拉普拉斯中心極限定理,以及他對常態分配和機率理論的研究。德莫佛還寫了一本機率理論的教科書,TheDoctrineofChances,據說這本書被投機主義者(gambler)高度讚揚。德莫佛是解析幾何和機率理論的先驅之一;他還最早發現了一個二項分布的近似公式,這一公式被認為是常態分配的首次露面。
大數法則又稱“大數定律”或“平均法則”。人們在長期的實踐中發現,在隨機現象的大量重複中往往出現幾乎必然的規律,即大數法則。此法則的意義是:風險單位數量愈多,實際損失的結果會愈接近從無限單位數量得出的預期損失可能的結果。據此,保險人就可以比較精確的預測危險,合理的厘定保險費率,使在保險期限內收取的保險費和損失賠償及其它費用開支相平衡。大數法則是近代保險業賴以建立的數理基礎。保險公司正是利用在個別情形下存在的不確定性將在大數中消失的這種規則性,來分析承保標的發生損失的相對穩定性。按照大數法則,保險公司承保的每類標的數目必須足夠大,否則,缺少一定的數量基礎,就不能產生所需要的數量規律。但是,任何一家保險公司都有它的局限性,即承保的具有同一風險性質的單位是有限的,這就需要通過再保險來擴大風險單位及風險分散面。
常見類型
由於隨機變數序列向常數的收斂有多種不同的形式,按其收斂為依機率收斂,以機率 1 收斂或均方收斂,分別有弱大數定律、強大數定律和均方大數定律。
常用的大數定律[1]有:伯努利大數定律、辛欽大數定律、柯爾莫哥洛夫強大數定律和重對數定律。
設有一隨機變數序列,假如它具有形如(1)的性質,則稱該隨機變數服從大數定律。
伯努利大數定律設為n重伯努利實驗中事件A發生的次數,p為每次實驗中A出現的機率,則對任意的ε>0,有(2)成立。切比雪夫大數定律設{Xn}為一列兩兩不相關的隨機變數序列,若每個Xn的方差存在,且有共同的上界,即Var(Xn)小於或等於c,則{Xn}服從大數定律,即對任意的ε>0,(1)式成立。馬爾可夫大數定律對隨機變數序列{Xn},若(3)成立,則{Xn}服從大數定律,即對任意的ε>0,(1)式成立。辛欽大數定律XnXnXn設{Xn}為獨立同分布的隨機變數序列,若的數學期望存在,則{Xn}服從大數定律,即對任意的ε>0,(1)成立。泊松大數定律如果在一個獨立試驗序列中,事件A在第k次試驗中出現的機率等於Pk,以Un記在前n次試驗中事件A出現的次數,則對任意ε>0,都有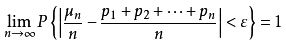 泊松大數定律
泊松大數定律
