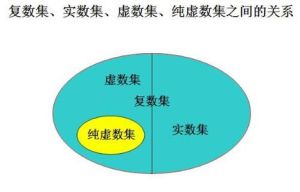
複數（complexnumber）為，形如a＋bi的數。式中a，b為實數，i是一個滿足i2＝－1的數，因為任何實數的平方不等於－1，所以i不是實數，而是實數以外的新的數。在複數a＋bi中，a稱為複數的實部，b稱為複數的虛部，i稱為虛數單位。當虛部等於零時，這個複數就是實數；當虛部不等於零時，這個複數稱為虛數，虛數的實部如果等於零，則稱為純虛數。由上可知，複數集包含了實數集，因而是實數集的擴張。
調和函式編輯定義：如圖所示：定理：如圖所示：對定理的證明過程，如圖所示：共軛調和函式：定義：如圖所示：定義的相關知識，如圖冊所示： 共軛調和函式關於定義的相關知識(4張)定理：如圖所示：定理公式推導過程，如圖所示：複數歷史
最早有關複數方根的文獻出於公元1世紀希臘數學家海倫，他考慮的是平頂金字塔不可能問題。
16世紀義大利米蘭學者卡當（JeromeCardan1501—1576）在1545年發表的《重要的藝術》一書中，公布了三次方程的一般解法，被後人稱之為“卡當公式”。他是第一個把負數的平方根寫到公式中的數學家，並且在討論是否可能把10分成兩部分，使它們的乘積等於40時，他把答案寫成
儘管他認為和這兩個表示式是沒有意義的、想像的、虛無飄渺的，但他還是把10分成了兩部分，並使它們的乘積等於40。給出“虛數”這一名稱的是法國數學家笛卡爾（1596—1650），他在《幾何學》（1637年發表）中使“虛的數”與“實的數”相對應，從此，虛數才流傳開來。
數系中發現一顆新星——虛數，於是引起了數學界的一片困惑，很多大數學家都不承認虛數。德國數學家萊布尼茨（1646—1716）在1702年說：“虛數是神靈遁跡的精微而奇異的隱避所，它大概是存在和虛妄兩界中的兩棲物”。瑞士數學大師歐拉（1707—1783）說：“一切形如，的數學式子都是不可能有的，想像的數，因為它們所表示的是負數的平方根。對於這類數，我們只能斷言，它們既不是什麼都不是，也不比什麼都不是多些什麼，更不比什麼都不是少些什麼，它們純屬虛幻。”然而，真理性的東西一定可以經得住時間和空間的考驗，最終占有自己的一席之地。法國數學家達朗貝爾（1717—1783）在1747年指出，如果按照多項式的四則運算規則對虛數進行運算，那么它的結果總是的形式（a、b都是實數）。法國數學家棣莫弗（1667—1754）在1730年發現了著名的棣莫佛定理。歐拉在1748年發現了有名的關係式，並且是他在《微分公式》（1777年）一文中第一次用i來表示-1的平方根，首創了用符號i作為虛數的單位。“虛數”實際上不是想像出來的，而它是確實存在的。挪威的測量學家成塞爾（1745—1818）在1779年試圖給於這種虛數以直觀的幾何解釋，並首先發表其作法，然而沒有得到學術界的重視。
十八世紀末，複數漸漸被大多數人接受，當時卡斯帕爾·韋塞爾提出複數可看作平面上的一點。數年後，高斯再提出此觀點並大力推廣，複數的研究開始高速發展。詫異的是，早於1685年約翰·沃利斯已經在DeAlgebratractatus提出此一觀點。
卡斯帕爾·韋塞爾的文章發表在1799年的ProceedingsoftheCopenhagenAcademy上，以當今標準來看，也是相當清楚和完備。他又考慮球體，得出四元數並以此提出完備的球面三角學理論。1804年，AbbéBuée亦獨立地提出與沃利斯相似的觀點，即以來表示平面上與實軸垂直的單位線段。1806年，Buée的文章正式刊出，同年讓-羅貝爾·阿爾岡亦發表同類文章，而阿岡的複平面成了標準。1831年高斯認為複數不夠普及，次年他發表了一篇備忘錄，奠定複數在數學的地位。柯西及阿貝爾的努力，掃除了複數使用的最後顧忌，後者更是首位以複數研究著名的。
複數吸引了著名數學家的注意，包括庫默爾（1844年）、克羅內克（1845年）、Scheffler（1845年、1851年、1880年）、Bellavitis（1835年、1852年）、喬治·皮庫克（1845年）及德·摩根（1849年）。莫比烏斯發表了大量有關複數幾何的短文，約翰·彼得·狄利克雷將很多實數概念，例如素數，推廣至複數。
德國數學家阿甘得（1777—1855）在1806年公布了虛數的圖象表示法，即所有實數能用一條數軸表示，同樣，虛數也能用一個平面上的點來表示。在直角坐標系中，橫軸上取對應實數a的點A，縱軸上取對應實數b的點B，並過這兩點引平行於坐標軸的直線，它們的交點C就表示複數。象這樣，由各點都對應複數的平面叫做“複平面”，後來又稱“阿甘得平面”。高斯在1831年，用實數組代表複數，並建立了複數的某些運算，使得複數的某些運算也象實數一樣地“代數化”。他又在1832年第一次提出了“複數”這個名詞，還將表示平面上同一點的兩種不同方法——直角坐標法和極坐標法加以綜合。統一於表示同一複數的代數式和三角式兩種形式中，並把數軸上的點與實數一一對應，擴展為平面上的點與複數一一對應。高斯不僅把複數看作平面上的點，而且還看作是一種向量，並利用複數與向量之間一一對應的關係，闡述了複數的幾何加法與乘法。至此，複數理論才比較完整和系統地建立起來了。
經過許多數學家長期不懈的努力，深刻探討並發展了複數理論，才使得在數學領域遊蕩了200年的幽靈——虛數揭去了神秘的面紗，顯現出它的本來面目，原來虛數不“虛”。虛數成為了數系大家庭中一員，從而實數集才擴充到了複數集。
隨著科學和技術的進步，複數理論已越來越顯出它的重要性，它不但對於數學本身的發展有著極其重要的意義，而且為證明機翼上升力的基本定理起到了重要作用，並在解決堤壩滲水的問題中顯示了它的威力，也為建立巨大水電站提供了重要的理論依據。
主要內容
形式
數集拓展到實數範圍內，仍有些運算無法進行。比如判別式小於0的一元二次方程仍無解，因此將數集再次擴充，達到複數範圍。
形如z=a+bi的數稱為複數（complexnumber)，其中規定i為虛數單位，且i²=i×i=－1（a，b是任意實數）
我們將複數z=a+bi中的實數a稱為複數z的實部（realpart)記作Rez=a
調和函式編輯定義：如圖所示：定理：如圖所示：對定理的證明過程，如圖所示：共軛調和函式：定義：如圖所示：定義的相關知識，如圖冊所示： 共軛調和函式關於定義的相關知識(4張)定理：如圖所示：定理公式推導過程，如圖所示：複數實數b稱為複數z的虛部（imaginarypart）記作Imz=b.
已知：當b=0時，z=a，這時複數成為實數；若且唯若a=b=0時，它是實數0；
當a=0且b≠0時，z=bi，我們就將其稱為純虛數。
複數的模
將複數的實部與虛部的平方和的正的平方根的值稱為該複數的模，記作∣z∣.
即對於複數z=a+bi，它的模
∣z∣=√（a^2+b^2)
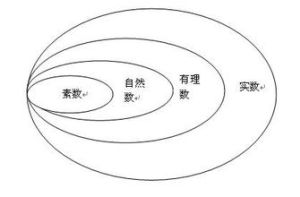
複數的集合用C表示，實數的集合用R表示，顯然，R是C的真子集。
複數集是無序集，不能建立大小順序。
產生
複數的產生來自解代數方程的需要。16世紀，義大利數學家G.卡爾達諾首先用公式表示出了一元三次方程的根，但公式中引用了負數開方的形式，並把i＝當作數，與其他數一起參與運算。由於人們無法理解的實質，所以在很長時間內不承認負數的平方根也是數，而稱之為虛數。直到19世紀，數學家們對這些虛數參與實數的代數運算作出了科學的解釋，並在解方程和其他領域中使虛數得到了廣泛的套用，人們才認識了這種新的數。
複數共軛複數
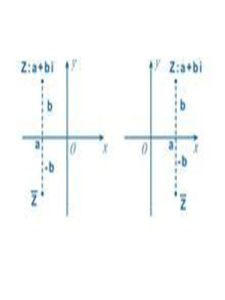
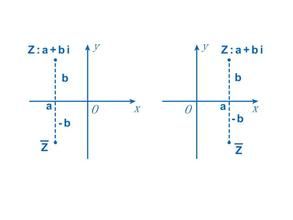
釋義對於複數z=a+bi，稱複數z'=a-bi為z的共軛複數。即兩個實部相等，虛部互為相反數的複數互為共軛複數(conjugatecomplexnumber）。複數z的共軛複數記作z'。表示方法為在字母z上方加一橫線即共軛符號。
性質
根據定義，若z=a+bi(a，b∈R），則zˊ=a－bi（a,b∈R）。共軛複數所對應的點關於實軸對稱。兩個複數：x+yi與x-yi稱為共軛複數,它們的實部相等，虛部互為相反數.在複平面上。表示兩個共軛複數的點關於X軸對稱，而這一點正是"共軛"一詞的來源。兩頭牛平行地拉一部犁，它們的肩膀上要共架一個橫樑，這橫樑就叫做"軛"。如果用Z表示X+Yi，那么在Z字上面加個"一"就表示X-Yi，或相反。
共軛複數有些有趣的性質：
︱x+yi︱=︱x-yi︱
(x+yi)*(x-yi)=x^2+y^2
複數的輻角
概述在複變函數中，自變數z可以寫成z=r*(cosθ+isinθ).r是z的模，即r=|z|;θ是z的輻角。在0到2π間的輻角稱為輻角主值，記作：arg（z）或者arc(z)
釋義
任意一個不為零的複數z=a+bi的輻角有無限多個值，且這些值相差2π的整數倍。把適合於-π<θ≤π的輻角θ的值，叫做輻角的主值，記作argz。輻角的主值是唯一的。且有Arg（z）=arg（z）+2kπ。
指數形式：。
四則運算
複數的四則運算規定為：
複數（a＋bi）＋（c＋di）＝（a＋c）＋（b＋d）i，
（a＋bi）－（c＋di）＝（a－c）＋（b－d）i，
（a＋bi）·（c＋di）＝（ac－bd）＋（bc＋ad）i，
（c與d不同時為零）。
表示形式
複數有多種表示形式，常用形式z＝a＋bi叫做代數式。此外有下列形式。
①幾何形式。複數z＝a＋bi用直角坐標平面上點Z（a，b）表示。這種形式使複數的問題可以藉助圖形來研究。也可反過來用複數的理論解決一些幾何問題。
②向量形式。複數z＝a＋bi用一個以原點O為起點，點Z（a，b）為終點的向量OZ表示。這種形式使複數的加、減法運算得到恰當的幾何解釋。
③三角形式。複數z＝a＋bi化為三角形式
z＝｜z｜（cosθ＋isinθ）式中｜z｜=，叫做複數的模（或絕對值）；θ是以x軸為始邊；向量OZ為終邊的角，叫做複數的輻角。這種形式便於作複數的乘、除、乘方、開方運算。
④指數形式。將複數的三角形式z＝｜z｜(cosθ＋isinθ）中的cosθ＋isinθ換為eiq，複數就表為指數形式
z＝｜z｜eiq，複數的乘、除、乘方、開方可以按照冪的運算法則進行。
複數複數集不同於實數集的幾個特點是：開方運算永遠可行；一元n次復係數方程總有n個根（重根按重數計）；複數不能建立大小順序。
複數與函式
單連/多連通域定義：複平面上的一個區域B，如果B內的任何簡單閉曲線的內部總在B內，就稱B為單連通域；非單連通域稱為多連通域。
1.複變函數的定義—與實變函式定義相類似
2.映射的概念——複變函數的幾何意義
在幾何上，w=f(z)可以看作：
複變函數的幾何意義是一個映射（變換）
在複變函數中用兩個複平面上點集之間的對應關係來表達兩對變數u，v與x，y之間的對應關係，以便在研究和理解複變函數問題時，可藉助於幾何直觀.
3.反函式或逆映射
定義設w=f(z)的定義集合為G,函式值集合為G*
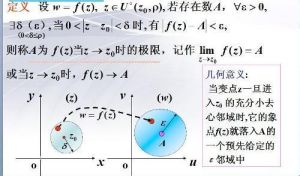
複數1.函式的極限
幾何意義:當變點z一旦進入z0的充分小去心鄰域時,它的象點f(z)就落入A的一個預先給定的ε鄰域中
(1)意義中Z→Z0的方式是任意的.與一元實變函式相比較要求更高.
(2)A是複數.
(3)若f(z)在Z0處有極限,其極限是唯一的.
2.運算性質
3.函式的連續性
導數定義
如果w=f(z)在區域D內處處可導，則稱f(z)在區域D內可導。
註：(1)Δz→0是在平面區域上以任意方式趨於零。
(2)z=x+iy,Δz=Δx+iΔy,Δf=f(z+Δz)-f(z)
2.求導公式與法則----實函式中求導法則的推廣①常數的導數c=(a+ib)=0.
②(zn)=nzn-1(n是自然數).
.............
分類
數的分類拓展到複數範圍後，我們對複數範圍的數集做以下分類複數（a+bi）——集合符號C
實數（b=0）——集合符號R
有理數——集合符號Q（p/q)
（一）正有理數——集合符號Q+
正整數——集合符號N+或N*
1--質數--合數正分數--0
－負有理數——集合符號Q-
複數－負整數——集合符號Z-
－負分數
（二）整數——集合符號Z
（自然數）——集合符號N--奇數--偶數--分數--無理數--正無理數--負無理數
－－虛數（b≠0)
－－純虛數（a=0)
－－混虛數（a≠0）
套用
系統分析在系統分析中，系統常常通過拉普拉斯變換從時域變換到頻域。因此可在複平面上分析系統的極點和零點。分析系統穩定性的根軌跡法、奈奎斯特圖法（Nyquistplot）和尼科爾斯圖法（Nicholsplot）都是在複平面上進行的。
無論系統極點和零點在左半平面還是右半平面，根軌跡法都很重要。如果系統極點
位於右半平面，則因果系統不穩定；都位於左半平面，則因果系統穩定；位於虛軸上，則系統為臨界穩定的。如果系統的全部零點和極點都在左半平面，則這是個最小相位系統。如果系統的極點和零點關於虛軸對稱，則這是全通系統。
信號分析
信號分析和其他領域使用複數可以方便的表示周期信號。模值|z|表示信號的幅度，輻角arg(z）表示給定頻率的正弦波的相位。
利用傅立葉變換可將實信號表示成一系列周期函式的和。這些周期函式通常用形式如下的複函數的實部表示：
其中ω對應角頻率，複數z包含了幅度和相位的信息。
電路分析中，引入電容、電感與頻率有關的虛部可以方便的將電壓、電流的關係用簡單的線性方程表示並求解。（有時用字母j作為虛數單位，以免與電流符號i混淆。）
反常積分
複數在套用層面，複分析常用以計算某些實值的反常函式，藉由復值函式得出。方法有多種，見圍道積分方法。
量子力學
量子力學中複數是十分重要的，因其理論是建基於複數域上無限維的希爾伯特空間。
相對論
如將時間變數視為虛數的話便可簡化一些狹義和廣義相對論中的時空度量(Metric)方程。
套用數學
實際套用中，求解給定差分方程模型的系統，通常首先找出線性差分方程對應的特徵方程的所有復特徵根r，再將系統以形為f(t)=e的基函式的線性組合表示。
流體力學
複函數於流體力學中可描述二維勢流(2DPotentialFlow）。
碎形
一些碎形如曼德勃羅集合和茹利亞集(Juliaset)是建基於複平面上的點的。
黎曼猜想軌跡
一，分解質數源數[開拓]：函式[]18rr+1]
1，r*6
2，18rr--r*6+1=0
二，整形第一部分
1，【[r1+r2]*6】*1/2=1
2，【18*[r1]*[r2]-[r1+r2]*6+1】*1/2=0
三，黎曼猜想化為[素數分布球體模式]
數系理論
引子
數系理論的歷史發展表明，數的概念的每一次擴張都標誌著數學的進步，但是這種進步並不是按照數學教科書的邏輯步驟展開的。希臘人關於無理數的發現暴露出有理數系的缺陷，而實數系的完備性一直要到19世紀才得以完成。負數早在《九章算術》中就已被中國數學家所認識，然而，15世紀的歐洲人仍然不願意承認負數的意義。“四元數”的發明，打開了通向抽象代數的大門，同時也宣告在保持傳統運算定律的意義下，複數是數系擴張的終點。人類發明的記數法並沒有束縛自己的想像力，中國古代“數窮則變”的思想對於當代數學哲學仍具有積極的意義。數，是數學中的基本概念，也是人類文明的重要組成部分。數的概念的每一次擴充都標誌著數學的巨大飛躍。一個時代人們對於數的認識與套用，以及數系理論的完善程度，反映了當時數學發展的水平。今天，我們所套用的數系，已經構造的如此完備和縝密，以致於在科學技術和社會生活的一切領域中，它都成為基本的語言和不可或缺的工具。在我們得心應手地享用這份人類文明的共同財富時，是否想到在數系形成和發展的歷史過程中，人類的智慧所經歷的曲折和艱辛呢？
十進制計數法
人類在進化的蒙昧時期，就具有了一種“識數”的才能，心理學家稱這種才能為“數覺”（perceptionofnumber）。動物行為學家則認為，這種“數覺”並非為人類所獨有。人類智慧的卓越之處在於他們發明了種種記數方法。《周易·繫辭下》記載“上古結繩而治，後世聖人，易之以書契”。東漢鄭玄稱：“事大，大結其繩；事小，小結其繩。結之多少，隨物眾寡”。以結繩和書契記數的方法實際上遍及世界各地，如希臘、波斯、羅馬、巴勒斯坦、伊斯蘭和中美洲國家都有文獻記載和實物標本。直到1826年，英國財政部才決定停止採用符契作為法定記數器。隨著人類社會的進步，數的語言也在不斷發展和完善。數系發展的第一個里程碑出現了：位置制記數法。所謂位置制記數法，就是運用少量的符號，通過它們不同個數的排列，以表示不同的數。引起歷史學家、數學史家興趣的是，在自然環境和社會條件影響下，不同的文明創造了迥然不同的記數方法。如巴比倫的楔形數字系統、埃及象形數字系統、希臘人字母數字系統、瑪雅數字系統、印度—阿拉伯數字系統和中國的算籌記數系統。
複數最早發展的一類數系應該是簡單分群數系（simplegroupingsystem），如在公元前3400年埃及象形文字中就有實例，它是10進的，但卻不是位置的。在公元前3000到2000年之間，巴比倫人發展了60進位的定位數系（positionalnumeralsystem），它採用了位置制，卻不是10進的。而最重要和最美妙的記數法則是10進位位置制記數法。
法國著名數學家拉普拉斯（Laplace,1749–1827）曾經寫道：
用十個記號來表示一切的數，每個記號不但有絕對的值，而且有位置的值，這種巧妙的方法出自印度。這是一個深遠而又重要的思想，它今天看來如此簡單，以致我們忽視了它的真正偉績。但恰恰是它的簡單性以及對一切計算都提供了極大的方便，才使我們的算術在一切有用的發明中列在首位；而當我們想到它竟逃過了古代最偉大的兩位人物阿基米德和阿波羅尼斯的天才思想的關注時，我們更感到這成就的偉大了。
拉普拉斯的這段評論十分精彩，只可惜他張冠李戴，把這項發明歸之於印度。現已有充分而確鑿的史料證明，10進位位置制記數法最先產生於中國。這一點也為西方的一些數學史家所主張。李約瑟就曾指出“在西方後來所習見的‘印度數字’的背後，位置制已在中國存在了兩千年。”不過，10進位位置制記數法的產生不能單純地歸結為天才的智慧。記數法的進步是與計算工具的改進相聯繫的。研究表明，10進位位置制記數之產生於中國，是與算籌的使用與籌算制度的演進分不開的。
“0”作為記數法中的空位，在位置制記數的文明中是不可缺少的。早期的巴比倫楔形文字和宋代以前的中國籌算記數法，都是留出空位而沒有符號。印度人起初也是用空位表示零，後來記成點號“·”，最後發展為圈號。印度數碼在公元8世紀傳入阿拉伯國家。13世紀初，義大利的商人斐波那契（LeonadoFibonacci,1175-1250）編著《算經》（LiberAbacci,1202），把包括零號在內完整的印度數碼介紹到了歐洲。印度數碼和10進位位置制記數法被歐洲人普遍接受後，在歐洲的科學和文明的進步中扮演了重要的角色。
大數記法
古代希臘人曾經提出一個問題：他們認為世界上的沙子是無窮的，即使不是無窮，也沒有一個可以寫出來的數超過沙子的數。阿基米德（Archimedes,BC287-212）的回答是：不。在《數沙術》中，阿基米德以萬（myriad）為基礎，建立新的記數法，使得任何大的數都能表示出來。他的做法是：從1起到1億（原文是萬萬，myriadmyriads，這裡按照中文的習慣改稱為億）叫做第1級數；以億（10^8）為第2級數的單位，從億起到億億（即10^16）叫做第2級數；在以億億為單位，直到億億億（10^24）叫做第3級數。直到第1億級數的最後一數億億。阿基米德算出充滿宇宙的沙子的數目不過是10^51，即使擴充到“恆星宇宙”，即以太陽到恆星的距離為半徑的天球，也不過只能容納10^63個沙粒！
大數記法 複數同樣的問題也出現在中國古代。漢代以前，數皆10進，以10萬為億。韋昭解《國語·鄭語》第十六：“計億事，材兆物，收經入，行垓極”。注稱“計，算也；材，裁也。賈唐說皆以萬萬為億，鄭後司農云：十萬曰億，十億曰兆，從古數也。”《數術記遺》中則詳細記載了對大數的一整套命名和三種進位方法。《數術記遺》稱：
黃帝為法，數有十等，及其用也，乃有三焉。十等者億、兆、京、垓、秭、壤、溝、澗、正、載；三等者，謂上、中、下也。其下數者。十十變之，若言十萬曰億，十億曰兆，十兆曰京也。中數者，萬萬變之，若言萬萬曰億、萬億曰兆，萬兆曰京。上數者，數窮則變，若言萬萬曰億，億億曰兆，兆兆曰京也。從億至載，終於大衍。
《數術記遺》中的“大數之法”的數學意義並不僅僅在於它構造了三種記數方法，更為重要的是它揭示了人們對數的認識從有限走向無限的艱難歷程。客觀的需要和數學的發展都促使人們去認識和把握越來越大的數。起初，對一些較大的數，人們還可以理解它，還能夠利用已有的記數單位去表示它。但是，隨著人們認識的發展，這些大數也在迅速的擴張，原有的記數單位難以為用。人們不禁要問：
數有窮乎？
這是數系發展中的需要回答的重大命題。《數術記遺》中記載的徐岳和他的老師劉洪的對話，精彩的闡明了“數窮則變”的深刻道理：
徐岳問曰：數有窮乎？
會稽（劉洪）答曰：吾曾游天目山中，見有隱者，世莫知其名，號曰天目先生，余亦以此意問之。先生曰：世人言三不能比兩，乃雲捐悶與四維。數不識三，妄談知十。不辨積微之為量，詎曉百億於大千？黃帝為法，數有十等。……從億至載，終於大衍。
會稽問曰：先生之言，上數者數窮則變，既雲終於大衍，大衍有限，此何得無窮？
先生答曰：數之為用，言重則變，以小兼大，又加循環。循環之理，且有窮乎！
天目先生的做法是藉助“以小兼大”的“循環之理”，以有限來認識無限，而指引這一途徑的重要思想是“言重則變”。即便是今日，“數窮則變”這一樸素的辯證思維所蘊涵的深邃哲理仍值得人們深思。
http://baike.baidu.com/picview/10078/12656510/0/8718367adab44aed9759dd35b31c8701a08bfbc8.html?fr=lemma有理數系
位置制記數法的出現，標誌著人類掌握的數的語言，已從少量的文字個體，發展到了一個具有完善運算規則的數系。人類第一個認識的數系，就是常說的“自然數系”。但是，隨著人類認識的發展，自然數系的缺陷也就逐漸顯露出來。首先，自然數系是一個離散的、而不是稠密的數系[2]，因此，作為量的表征，它只能限於去表示一個單位量的整數倍，而無法表示它的部分。同時，作為運算的手段，在自然數系中只能施行加法和乘法，而不能自由地施行它們的逆運算。這些缺陷，由於分數和負數的出現而得以彌補。有趣的是這些分數也都帶有強烈的地域特徵。巴比倫的分數是60進位的，埃及採用的是單分數（unitfraction），阿拉伯的分數更加複雜：單分數、主分數和複合分數。這種繁複的分數表示必然導致分數運算方法的繁雜，所以歐洲分數理論長期停滯不前，直到15世紀以後才逐步形成現代的分數算法。與之形成鮮明對照的是中國古代在分數理論上的卓越貢獻。
原始的分數概念來源於對量的分割。如《說文·八部》對“分”的解釋：“分，別也。從八從刀，刀以分別物也。”但是，《九章算術》中的分數是從除法運算引入的。其“合分術”有云：“實如法而一。不滿法者，以法命之。”這句話的今譯是：被除數除以除數。如果不能除盡，便定義了一個分數。中國古代分數理論的高明之處是它藉助於“齊同術”把握住了分數算法的精髓：通分。劉徽在《九章算術注》中所言：
複數眾分錯雜，非細不會。乘而散之，所以通之。通之則可並也。凡母互乘子謂之齊，群母相乘謂之同。同者，相與通同共一母也。齊者，子與母齊，勢不可失本數也。
有了齊同術，就可將分數化異類為同類，變相違為相通。劉徽深得其中奧秘，稱：“然則齊同之術要矣。錯綜度數，動之斯諧，其猶佩?解結，無往而不理焉。乘以散之，約以聚之，齊同以通之，此其算之綱紀乎。”
容易證明，分數系是一個稠密的數系，它對於加、乘、除三種運算是封閉的。為了使得減法運算在數系內也同行無阻，負數的出現就是必然的了。盈餘與不足、收入與支出、增加與減少是負數概念在生活中的實例，教科書在向學生講授負數是也多循此途。這就產生一種誤解：似乎人類正是從這種具有相反意義的量的認識而引進了負數的。歷史的事實表明：負數之所以最早為中算家所引進，這是由中國古代傳統數學中，算法高度發達和籌算機械化的特點所決定的。負數的概念和算法首先出現在《九章算術》“方程”章，因為對“方程”進行兩行之間的加減消元時，就必須引入負數和建立正負數的運算法則。劉徽的注釋深刻的闡明了這點：
負數
今兩算得失相反，要令正負以名之。正算赤，負算黑，否則以斜正為異。方程自有赤黑相取，左右數相推求之術。而其並減之勢不得廣通，故使赤黑相消奪之。……故赤黑相雜足以定上下之程，減益雖殊足以通左右之數，差實雖分足以應同異之率。然則其正無入負之，負無入正之，其率不妄也。負數雖然通過阿拉伯人的著作傳到了歐洲，但16世紀和17世紀的大多數數學家並不承認它們是數，或者即使承認了也並不認為它們是方程的根。如丘凱（NicolasChuquet，）和斯蒂費爾（Stifel,）都把負數說成是荒謬的數，是“無稽之零下”。卡丹（Cardan,1501-1576)把負數作為方程的根，但認為它們是不可能的解，僅僅是一些記號；他把負根稱作是虛有的。韋達(Vieta,1540-1630)完全不要負數，帕斯卡（Pascal,1623-1662）則認為從0減去4純粹是胡說。
負數是人類第一次越過正數域的範圍，前此種種的經驗，在負數面前全然無用。在數系發展的歷史進程中，現實經驗有時不僅無用，反而會成為一種阻礙。我們將會看到，負數並不是惟一的例子。
無理數
無理數的發現，擊碎了畢達哥拉斯（Pythagoras）學派“萬物皆數”的美夢。同時暴露出有理數系的缺陷：一條直線上的有理數儘管是“稠密”，但是它卻漏出了許多“孔隙”，而且這種“孔隙”多的“不可勝數”。這樣，古希臘人把有理數視為是連續銜接的那種算術連續統的構想，就徹底的破滅了。它的破滅，在以後兩千多年時間內，對數學的發展，起到了深遠的影響。不可通約的本質是什麼？長期以來眾說紛紜。兩個不可通約量的比值也因其得不到正確的解釋，而被認為是不可理喻的數。15世紀達文西（LeonardodaVinci,1452-1519）把它們稱為是“無理的數”（irrationalnumber），克卜勒（J.Kepler,1571-1630）稱它們是“不可名狀”的數。這些“無理”而又“不可名狀”的數，找到雖然在後來的運算中漸漸被使用，但是它們究竟是不是實實在在的數，卻一直是個困擾人的問題。中國古代數學在處理開方問題時，也不可避免地碰到無理根數。對於這種“開之不盡”的數，《九章算術》直截了當地“以面命之”予以接受，劉徽注釋中的“求其微數”，實際上是用10進小數來無限逼近無理數。這本是一條完成實數系統的正確道路，只是劉徽的思想遠遠超越了他的時代，而未能引起後人的重視。不過，中國傳統數學關注的是數量的計算，對數的本質並沒有太大的興趣。而善於究根問底的希臘人就無法邁過這道坎了，既然不能克服它，那就只好迴避它。此後的希臘數學家，如歐多克斯（Eudoxus）、歐幾里得（Euclid）在他們的幾何學裡，都嚴格避免把數與幾何量等同起來。歐多克斯的比例論（見《幾何原本》第5卷），使幾何學在邏輯上繞過了不可公度的障礙，但就在這以後的漫長時期中，形成了幾何與算術的顯著分離。
17、18世紀微積分的發展幾乎吸引了所有數學家的注意力，恰恰是人們對微積分基礎的關注，使得實數域的連續性問題再次突顯出來。因為，微積分是建立在極限運算基礎上的變數數學，而極限運算，需要一個封閉的數域。無理數正是實數域連續性的關鍵。
無理數是什麼？法國數學家柯西（A.Cauchy,1789-1875）給出了回答：無理數是有理數序列的極限。然而按照柯西的極限定義，所謂有理數序列的極限，意即預先存在一個確定的數，使它與序列中各數的差值，當序列趨於無窮時，可以任意小。但是，這個預先存在的“數”，又從何而來呢？在柯西看來，有理序列的極限，似乎是先驗地存在的。這表明，柯西儘管是那個時代大分析學家，但仍未能擺脫兩千多年來以幾何直覺為立論基礎的傳統觀念的影響。
變數數學獨立建造完備數域的歷史任務，終於在19世紀後半葉，由維爾斯特拉斯（Weierstrass,1815-1897）、戴德金（R.Dedekind1831-1916）、康托（G.Cantor,1845-1918）等人加以完成了。
1872年，是近代數學史上最值得紀念的一年。這一年，克萊因（F.Kline,1849-1925）提出了著名的“埃爾朗根綱領”（ErlangerProgramm），維爾斯特拉斯給出了處處連續但處處不可微函式的著名例子。也正是在這一年，實數的三大派理論：戴德金“分割”理論；康托的“基本序列”理論，以及維爾斯特拉斯的“有界單調序列”理論，同時在德國出現了。
努力建立實數的目的，是為了給出一個形式化的邏輯定義，它既不依賴幾何的含義，又避免用極限來定義無理數的邏輯錯誤。有了這些定義做基礎，微積分中關於極限的基本定理的推導，才不會有理論上的循環。導數和積分從而可以直接在這些定義上建立起來，免去任何與感性認識聯繫的性質。幾何概念是不能給出充分明白和精確的，這在微積分發展的漫長歲月的過程中已經被證明。因此，必要的嚴格性只有通過數的概念，並且在割斷數的概念與幾何量觀念的聯繫之後才能完全達到。這裡，戴德金的工作受到了崇高的評價，這是因為，由“戴德金分割”定義的實數，是完全不依賴於空間與時間直觀的人類智慧的創造物。
實數的三大派理論本質上是對無理數給出嚴格定義，從而建立了完備的實數域。實數域的構造成功，使得兩千多年來存在於算術與幾何之間的鴻溝得以完全填平，無理數不再是“無理的數”了，古希臘人的算術連續統的構想，也終於在嚴格的科學意義下得以實現。
複數
複數概念的進化是數學史中最奇特的一章，那就是數系的歷史發展完全沒有按照教科書所描述的邏輯連續性。人們沒有等待實數的邏輯基礎建立之後，才去嘗試新的征程。在數系擴張的歷史過程中，往往許多中間地帶尚未得到完全認識，而天才的直覺隨著勇敢者的步伐已經到達了遙遠的前哨陣地。1545年，此時的歐洲人尚未完全理解負數、無理數，然而他們智力又面臨一個新的“怪物”的挑戰。例如卡丹在所著《重要的藝術》（1545）中提出一個問題：把10分成兩部分，使其乘積為40。這需要解方程x(10-x)=40，他求得的根是5-√-15和5+√-15，然後說“不管會受到多大的良心責備，”把5+√-15和5-√-15相乘，得到25-(-15)=40。於是他說，“算術就是這樣神妙地搞下去，它的目標，正如常言所說，是有精緻又不中用的。”笛卡爾（Descartes,1596-1650）也拋棄復根，並造出了“虛數”（imaginarynumber）這個名稱。對複數的模糊認識，萊布尼茲（Leibniz,1646-1716）的說法最有代表性：“聖靈在分析的奇觀中找到了超凡的顯示，這就是那個理想世界的端兆，那個介於存在與不存在之間的兩棲物，那個我們稱之為虛的—1的平方根。”
直到18世紀，數學家們對複數才稍稍建立了一些信心。因為，不管什麼地方，在數學的推理中間步驟中用了複數，結果都被證明是正確的。特別是1799年，高斯（Gauss,1777-1855）關於“代數基本定理”的證明必須依賴對複數的承認，從而使複數的地位得到了近一步的鞏固。當然，這並不是說人們對“複數”的顧慮完全消除了。甚至在1831年，棣莫甘（DeMorgan,1806-1871）在他的著作《論數學的研究和困難》中依然認為：
"……
已經證明了記號是沒有意義的，或者甚至是自相矛盾或荒唐可笑的。然而，通過這些記號，代數中極其有用的一部分便建立起來的，它依賴於一件必須用經驗來檢驗的事實，即代數的一般規則可以套用於這些式子（複數）。
……"
我們知道，18世紀是數學史上的“英雄世紀”，人們的熱情是如何發揮微積分的威力，去擴大數學的領地，沒有人會對實數系和複數系的邏輯基礎而操心。既然複數至少在運算法則上還是直觀可靠的，那又何必去自找麻煩呢？
1797年，挪威的韋塞爾（C.Wessel,1745-1818）寫了一篇論文“關於方向方向的分析表示”，試圖利用向量來表示複數，遺憾的是這篇文章的重大價值直到1897年譯成法文後，才被人們重視。瑞士人阿甘達（J.Argand,1768-1822）給出複數的一個稍微不同的幾何解釋。他注意到負數是正數的一個擴張，它是將方向和大小結合起來得出的，他的思路是：能否利用新增添某種新的概念來擴張實數系？在使人們接受複數方面，高斯的工作更為有效。他不僅將a+bi表示為複平面上的一點(a,b），而且闡述了複數的幾何加法和乘法。他還說，如果1，-1和原來不稱為正、負和虛單位，而稱為直、反和側單位，那么人們對這些數就可能不會產生種種陰暗神秘的印象。他說幾何表示可以使人們對虛數真正有一個新的看法，他引進術語“複數”（complexnumber）以與虛數相對立，並用i代替。
在澄清複數概念的工作中，愛爾蘭數學家哈米爾頓（Hamilton,1805–1865）是非常重要的。哈米爾頓所關心的是算術的邏輯，並不滿足於幾何直觀。他指出：複數a+bi不是2+3意義上的一個真正的和，加號的使用是歷史的偶然，而bi不能加到a上去。複數a+bi只不過是實數的有序數對（a，b），並給出了有序數對的四則運算，同時，這些運算滿足結合律、交換率和分配率。在這樣的觀點下，不僅複數被邏輯地建立在實數的基礎上，而且至今還有點神秘的-1的平方根也完全消除了。
http://baike.baidu.com/picview/10078/12656510/0/8718367adab44aed9759dd35b31c8701a08bfbc8.html?fr=lemma四元數
回顧數系的歷史發展，似乎給人這樣一種印象：數系的每一次擴充，都是在舊的數系中添加新的元素。如分數添加於整數，負數添加於正數，無理數添加於有理數，複數添加於實數。但是，現代數學的觀點認為：數系的擴張，並不是在舊的數系中添加新元素，而是在舊的數系之外去構造一個新的代數系，其元素在形式上與舊的可以完全不同，但是，它包含一個與舊代數系同構的子集，這種同構必然保持新舊代數系之間具有完全相同的代數構造。當人們澄清了複數的概念後，新的問題是：是否還能在保持複數基本性質的條件下對複數進行新的擴張呢？答案是否定的。當哈米爾頓試圖尋找三維空間複數的類似物時，他發現自己被迫要做兩個讓步：第一，他的新數要包含四個分量；第二，他必須犧牲乘法交換律。這兩個特點都是對傳統數系的革命。他稱這新的數為“四元數”。“四元數”的出現昭示著傳統觀念下數系擴張的結束。1878年，富比尼（F.Frobenius,1849–1917)證明：具有有限個原始單元的、有乘法單位元素的實係數先行結合代數，如果服從結合律，那就只有實數，複數和實四元數的代數。
四元數 數學的思想一旦衝破傳統模式的藩籬，便會產生無可估量的創造力。哈米爾頓的四元數的發明，使數學家們認識到既然可以拋棄實數和複數的交換性去構造一個有意義、有作用的新“數系”，那么就可以較為自由地考慮甚至偏離實數和複數的通常性質的代數構造。數系的擴張雖然就此終止，但是，通向抽象代數的大門被打開了。
初等函式
實變初等函式
我們把數學分析中基本的實變初等函式推廣到復變初等函式，使得定義的各種復變初等函式，當z變為實變數x(y=0）時與相應的實變初等函式相同。注意根據這些定義，在z為任意復變數時，
複數①．哪些相應的實變初等函式的性質被保留下來
②．哪些相應的實變初等函式的性質不再成立
③．出現了哪些相應的實變初等函式所沒有的新的性質。
復變指數函式
e^(a+bi)=e^a*e^bi=e^a*(cosb+isinb)複數的三角函式
證明：把yi代入泰勒級數，藉助sinx=x-x^3/3!+x^5/5!-...(-1)^(k-1)*x^(2k-1)/(2k-1)!+Rn(x）和cosx=1-x^2/2!+x^4/4!-...(-1)^k*x^(2k)/(2k)!+...+Rn(x）來化簡即可；
同理可得a^ix=cos(xlna)+isin(xlna)=(e^ix)^lna.
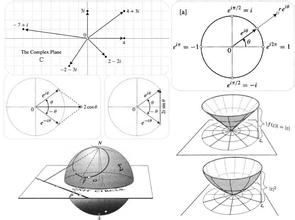複數藉助e^ix=cosx+isinx可以方便地證明棣莫佛定理
公式口決
虛數單位i一出，數集擴大到複數。一個複數一對數，橫縱坐標實虛部。對應複平面上點，原點與它連成箭。箭桿與X軸正向，所成便是輻角度。
箭桿的長即是模，常將數形來結合。代數幾何三角式，相互轉化試一試。
代數運算的實質，有i多項式運算。i的正整數次冪，四個數值周期現。
一些重要的結論，熟記巧用得結果。虛實互化本領大，複數相等來轉化。
利用方程思想解，注意整體代換術。幾何運算圖上看，加法平行四邊形，
減法三角法則判;乘法除法的運算，逆向順向做鏇轉，伸縮全年模長短。
三角形式的運算，須將輻角和模辨。利用棣莫弗公式，乘方開方極方便。
輻角運算很奇特，和差是由積商得。四條性質離不得，相等和模與共軛，
兩個不會為實數，比較大小要不得。複數實數很密切，須注意本質區別。
