分類
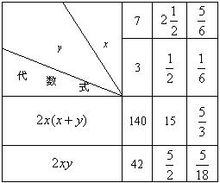 代數式
代數式在實數範圍內,代數式分為有理式和無理式。
有理式有理式包括整式(除數中沒有字母的有理式)和分式(除數中有字母且除數不為0的有理式)。這種代數式中對於字母只進行有限次加、減、乘、除和整數次乘方這些運算.
整式有包括單項式(數字或字母的乘積或單獨的一個數字或字母)和多項式(若干個單項式的和)。
1、單項式
沒有加減運算的整式叫做單項式。
單項式的係數:單項式中的數字因數叫做單項式(或字母因數)的數字係數,簡稱係數。
單項式的次數:一個單項式中,所有字母的指數的和叫做這個單項式的次數。
2、多項式
幾個單項式的代數和叫做多項式;多項式中每個單項式叫做多項式的項。不含字母的項叫做常數項。
多項式的次數:多項式里,次數最高的項的次數,就是這個多項式的次數。齊次多項式:各項次數相同的多項式叫做齊次多項式。不可約多項式:次數大於零的有理係數的多項式,不能分解為兩個次數大於零的有理數係數多項式的乘積時,稱為有理數範圍內不可約多項式。實數範圍內不可約多項式是一次或某些二次多項式,複數范同內不可約多項式是一次多項式。對稱多項式:在多元多項式中,如果任意兩個元互相交換所得的結果都和原式相同,則稱此多項式是關於這些元的對稱多項式。同類項:多項式中含有相同的字母,並且相同字母的指數也分別相同的項叫做同類項。
無理式
含有字母的根式或字母的非整數次乘方的代數式叫做無理式。
書寫格式
兩字母相乘、數字與字母相乘、字母與括弧相乘以及括弧與括弧相乘時,乘號都可以省略不寫.如:“x與y的積”可以寫成“xy”;“a與2的積”應寫成“2a”,“m、n的和的2倍”應寫成“2(m+n)”。
字母與數字相乘或數字與括弧相乘時,乘號可省略不寫,但數字必須寫在前面.例如“x×2”要寫成”2x”,不能寫成“x2”;“長、寬分別為a、b的長方形的周長”要寫成“2(a+b)”,不能寫成“(a+b)2”。
代數式中不能出現除號,相除關係要寫成分數的形式
數字與數字相乘時,乘號(也可以寫作 · )仍應保留不能省略,或直接計算出結果.例如“3×7xy”不能寫成“37xy”,最好寫成“21xy”。
數式的運算
合併同類項:把多項式中同類項合併成一項,叫做合併同類項。合併同類項的法則是:同類項的係數相加,所得的結果作為係數,字母和字母的指數不變。
去括弧法則:括弧前足“+”號,把括弧和它前面的“+”號去掉,括弧里各項都不變符號;括弧前是“—”號,把括弧和它前面的“—”號去掉,括弧里各項都改變符號。
添括弧法則:添括導後,括弧前面是“+”號,括到括弧里的各項都不變符號;添括弧後,括弧前面是“—”號,括到括弧里的各項都改變符號。
產生
 代數式
代數式產生在古代,當算術里積累了大量的,關於各種數量問題的解法後,為了尋求有系統的、更普遍的方法,以解決各種數量關係的問題,就產生了以解方程的原理為中心問題的初等代數。
代數是由算術演變來的,這是毫無疑問的。至於什麼年代產生的代數學這門學科,就很不容易說清楚了。比如,如果你認為“代數學”是指解bx+k=0這類用符號表示的方程的技巧。那么,這種“代數學”是在十六世紀才發展起來的。
如果我們對代數符號不是要求象現在這樣簡練,那么,代數學的產生可上溯到更早的年代。西方人將公元前三世紀古希臘數學家刁藩都看作是代數學的鼻祖。而在中國,用文字來表達的代數問題出現的就更早了。
“代數”作為一個數學專有名詞、代表一門數學分支在我國正式使用,最早是在1859年。那年,清代數學家裡李善蘭和英國人韋列亞力共同翻譯了英國人棣么甘所寫的一本書,譯本的名稱就叫做《代數學》。當然,代數的內容和方法,我國古代早就產生了,比如《九章算術》中就有方程問題。
初等代數的中心內容是解方程,因而長期以來都把代數學理解成方程的科學,數學家們也把主要精力集中在方程的研究上。它的研究方法是高度計算性的。
要討論方程,首先遇到的一個問題是如何把實際中的數量關係組成代數式,然後根據等量關係列出方程。所以初等代數的一個重要內容就是代數式。由於事物中的數量關係的不同,大體上初等代數形成了整式、分式和根式這三大類代數式。代數式是數的化身,因而在代數中,它們都可以進行四則運算,服從基本運算定律,而且還可以進行乘方和開方兩種新的運算。通常把這六種運算叫做代數運算,以區別於只包含四種運算的算術運算。
在初等代數的產生和發展的過程中,通過解方程的研究,也促進了數的概念的進一步發展,將算術中討論的整數和分數的概念擴充到有理數的範圍,使數包括正負整數、正負分數和零。這是初等代數的又一重要內容,就是數的概念的擴充。
有了有理數,初等代數能解決的問題就大大的擴充了。但是,有些方程在有理數範圍內仍然沒有解。於是,數的概念在一次擴充到了實數,進而又進一步擴充到了複數。
那么到了複數範圍內是不是仍然有方程沒有解,還必須把複數再進行擴展呢?數學家們說:不用了。這就是代數裡的一個著名的定理—代數基本定理。這個定理簡單地說就是n次方程有n個根。1742年12月15日瑞士數學家歐拉曾在一封信中明確地做了陳述,後來另一個數學家、德國的高斯在1799年給出了嚴格的證明。

