基本介紹
設(P,≤)是任意一個偏序集,考慮下述條件:
A極小條件:P中任意非空子集一定有極小元。
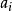 極小條件
極小條件B降鏈條件:P中任意元素列{ |i=1,2...}如果能組成一個降鏈,
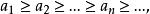 極小條件
極小條件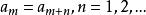 極小條件
極小條件則存在一個正整數m,使得 。
C歸納條件:對於任意一種性質ε,若
(1)P中一切極小元(當它們存在時)具有性質ε;
(2)對於任意a∈P,如果一切真小於a的元素都具有性質ε,可推得a也具有性質ε,則P中所有元素都具有性質ε。
對偶地,可有:
A'極大條件:P中任意非空子集一定有極大元;
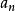 極小條件
極小條件B'升鏈條件:P中任意元素列{ |n=1,2...}如果能組成一個升鏈,即
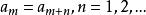 極小條件
極小條件 極小條件
極小條件則存在一個正整數m,使得。
C'對偶歸納條件:對於任意一種性質ε,若
(1)P中一切極大元(當它們存在時)具有性質ε;
(2)對於任意a∈P,如果一切真大於a的元素都具有性質ε,可推得a也具有性質ε,則P中所有元素都具有性質ε。
相關定理
定理1 對於任何偏序集(P.≤),條件A,B,C(對偶地:A',B',C')彼此等價。
證明 A→C設P滿足極小條件,ε是某一性質,並且歸納條件的前提成立,令
M={a|a∈P且a不具有性質ε},
則M⊆P,若M≠∅,由A知M中有一極小元a∈M,根據歸納條件的前提,a不是P中的極小元,但是一切真比a小的元素不在M中,因而具有性質ε,由歸納條件的第二個前提推得a也具有性質ε,這與a∈M矛盾,故M=∅,即C成立。
C→B設P滿足歸納條件,規定;
元素a(a∈P)具有性質ε若且唯若任意由a開始的降鏈:
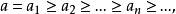 極小條件
極小條件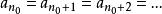 極小條件
極小條件必穩定在有限項,即存在正整數n,使得 ,顯然,P中一切極小元(當它們存在時)具有性質ε,設a∈P,並且所有真比a小的元素都具有性質ε,易證a亦具有性質ε,由C知P中所有元素都具有性質ε,故B成立。
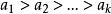 極小條件
極小條件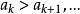 極小條件
極小條件B→A設B成立,若A不成立,則存在N⊆P,N≠∅,N無極小元。顯然N是無限集,任取a∈N,a不會是N的極小元,因此存在a∈N使得a>a,...假定已經找到a,a,...,a∈N,並且 ,顯然a也不是N的極小元,於是存在a∈N,使得 ,這樣繼續下去可得N中一列元素:
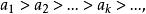 極小條件
極小條件此與條件B矛盾,故A成立。
利用對偶原則知A',B',C'彼此等價。
歸納條件不僅使我們可依歸納法去進行證明,也可用歸納法來構造。
定理2 設(P,≤)是滿足極小條件的偏序集,W是任意給定的集合.則存在惟一的映射φ:P→W,滿足條件:
(1)在P的所有極小元上φ取給定的值;
(2)φ滿足給定的逆推關係,即對任意的a∈P,φ(a)由所有真小乾a的元素b(b<a)的值φ(b)惟一決定。
定理3 設(P,≤)是任意偏序集,則P滿足極小條件若且唯若P內的所有鏈都是良序集。
若(P,≤)是一個偏序集,a∈P,稱P的子集
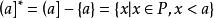 極小條件
極小條件為由a決定的 開截段,相應地,(a]叫做由a決定的 閉截段(或截段).
定理4設(P,≤)是一個良序集,A⊂P,則有
 極小條件
極小條件(1)A是P的上集 存在a∈P,使得A=(a]* ;(特別,∅是P的開截段);
 極小條件
極小條件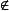 極小條件
極小條件(2)a≤b(∀a,b∈P) b (a]*;
(3)若在P上添加一個最大元I*(I*∈P),記P* =P∪{I*},規定a≤I*(∀a∈P*),而P中元素保持原來的序關係,則P*也是良序集。

