簡介
極小極大原理是用來確定泛函的臨界點存在性的一個較為一般的原理。
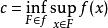 極小極大原理
極小極大原理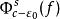 極小極大原理
極小極大原理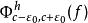 極小極大原理
極小極大原理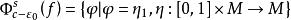 極小極大原理
極小極大原理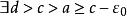 極小極大原理
極小極大原理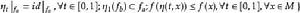 極小極大原理
極小極大原理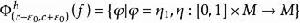 極小極大原理
極小極大原理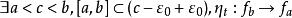 極小極大原理
極小極大原理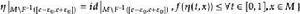 極小極大原理
極小極大原理設M是完備的C芬斯勒流形,f∈C(M,R)滿足(P.S)條件,是M的一一個非空子集族。記 若c是有限數,且存在ε>0,使得關於收縮映射族 或同胚映射族 是不變的,則c是f的臨界值,其中 是形變, ,使 是合痕, 同胚, 子集族稱為關於映射族φ是不變的,指的是∀F∈ ,∀φ∈⧲,有φ(F)∈。
推廣
上述原理中的(P.S)條件還可減弱。在實用中靈活選取子集族與映射族⧲可得到不同的臨界點存在定理。
泛函
簡單的說, 泛函就是定義域是一個函式集,而值域是實數集或者實數集的一個子集,推廣開來, 泛函就是從任意的向量空間到標量的映射。也就是說,它是從函式空間到數域的映射。
設{y}是給定的函式集,如果對於這個函式集中任一函式y(x) 恆有某個確定的數與之對應,記為П(y(x)),則П(y(x))是定義於集合{y(x)}上的一個泛函。
泛函定義域內的函式為可取函式或容許函式, y(x) 稱為泛函П的變數函式。
