解析函式邊界性質

解析函式邊界性質

正文

以複變函數論為基礎結合實變函式論研究解析函式的邊界性質，與調和函式的邊界性質有緊密的聯繫，主要研究單位圓內和一般區域內種種解析函式族的邊界性質。
設函式ƒ(z)在單位圓｜z｜< 1內解析，記

如果0<p ≤∞，Mp(r，ƒ)對一切0≤r<1有界，稱ƒ(z)屬於哈代函式族Hp；如果

對一切0≤r<1有界，稱ƒ(z)屬於奈望林納函式族N,這裡，若α≥1，log+α=logα；若α<1，log+α=0。
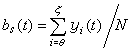
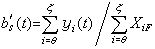
設ƒ(z)是平面區域D內的解析函式,ζ是邊界дD上的給定點,如果當z在D內以ζ為頂點的任何角形區域內趨於ζ時，ƒ(z)都趨向於一確定值,稱ƒ(z)在邊界點ζ處有非切向極限值,記為ƒ(ζ)。如果在 дD上除一測度為零的點集外，處處有非切向極限值，稱ƒ(z)在дD上幾乎處處有非切向邊界值ƒ(ζ)。
邊界性質與域內性質　一類問題是，利用解析函式的域內性質（比如函式模在區域內的增長性）研究其邊界性質。P.J.L.法圖(1906)和F.（F.）里斯(1923)分別對p=∞和0<p<∞證明：若ƒ(z)∈Hp,則ƒ(z)幾乎處處有非切向邊界值 ƒ(eiθ),|ƒ(eiθ)|∈Lp【0,2π】,log|ƒ(eiθ)|∈l1【0,2π】除非ƒ(z)呏0，並且對【0,2π】上的任何正測度集E，

1922年R.奈望林納證明：若ƒ(z)∈N且ƒ(z)扝0,則ƒ(z)幾乎處處有非切向邊界值ƒ(eiθ),並且log|ƒ(eiθ)|∈l1【0，2π】。另一類問題是,利用解析函式的邊界性質判斷其域內性質。1917年И.И.普里瓦洛夫證明：設ƒ(z)在|z|<1內解析,ƒ(z)扝0,若在單位圓周的一個正測度集E上,其非切向邊界值ƒ(eiθ)為零,則ƒ(z)呏0。又若ƒ(z)∈h1,則ƒ(z)在圓內的值可通過圓周的一個正測度集E上的邊界值表示出來。這是Γ.М.戈盧津和Β.И.克雷洛夫1933年的結果。
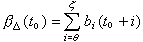
積分表示問題　單位圓|z|<1內解析函式 ƒ(z)可表示成φ∈lp【0,2π】(1≤p ≤∞)的泊松積分

的充分必要條件是：ƒ(z)∈Hp。
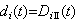
構造問題　里斯在1923年證明：若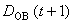且ƒ(z)扝0,則ƒ(z)=B(z)F(z),這裡B(z)是ƒ(z)在|z|<1內所有零點{zn}所組成的W.J.E.布拉施克乘積，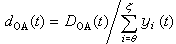

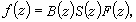
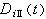
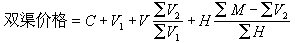F(z)∈Hp且F(z)≠0；若ƒ（z）∈N，則ƒ(z)=B(z)g(z)，g(z)∈N且g(z)≠0。1929年 Β.И.斯米爾諾夫進一步證明，單位圓內解析函式ƒ(z)∈Hp(p>0)的充要條件是：ƒ(z)可以分解成

這裡B(z)是ƒ的布拉施克乘積,S(z)是奇異內函式,F(z)是Hp的外函式，並且

式中m是非負整數，；μ(t)是非減的有界變差函式，其導函式幾乎處處等於零；ψ（t）>0,ψ∈lp，Inψ(t)∈l1【0,2π】，у是一實數。特別當ƒ∈hp時，ψ(t)幾乎處處等於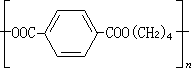。這種分解還是惟一的。又單位圓內解析函式ƒ(z)∈N的充要條件是ƒ(z)可分解成

，

這裡B(z)是ƒ的布拉施克乘積，S1(z)和S2(z)分別是奇異內函式,F(z)是N的外函式，其中ψ(t)≥0，lnψ(t)∈l1【0，2π】。特別若ƒ∈N，則ψ(t)幾乎處處等於。
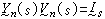一般區域的情形　設D是邊界多於一點的單連區域，若在D記憶體在可求長的若爾當閉曲線C1，C2,…,{Cn}趨於邊界дD，使得

，

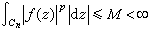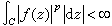則稱ƒ∈Ep（D）。若邊界是可求長的若爾當曲線C，則Ep(D)中每個函式ƒ(z)在C上幾乎處處有邊界值ƒ(ζ),並且；如果邊界值函式ƒ(ζ)在一正測度集上等於零,則ƒ(z)在D內必為零。若ƒ∈E1(D),則對D內的z,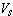；反之，若g在C上可積,並且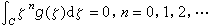,則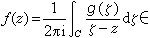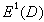，且在C上幾乎處處以g(ζ)為邊界值。
解析函式邊界性質的理論是Hp 空間理論的基礎和重要組成部分，對多復變數解析（全純）函式邊界性質的研究有深刻的影響，在奇異積分方程、解析函式的邊值問題和彈性力學及斷裂力學中都有廣泛套用。

配圖

相關連線