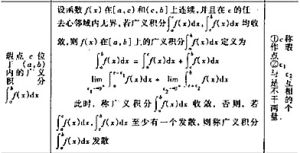廣義函式

廣義函式，數學概念，是古典函式概念的推廣。關於廣義函式的研究構成了泛函分析中有著廣泛套用的一個重要分支。廣義函式被廣泛地套用於數學、物理、力學以及分析數學的其他各個分支，例如微分方程、隨機過程、流形理論等等，它還被套用到群的表示理論，特別是它有力地促進了偏微分方程近30年來的發展。

基本信息

• 中文名：廣義函式
• 英文名：generalized function、distribution

• 解釋：是古典函式概念
• 套用：數學、物理、力學

來歷

廣義函式

古典函式概念的推廣。歷史上第一個廣義函式是由物理學家P.A.M.狄拉克引進的，他因為陳述量子力學中某些量的關係時需要引入了“函式”δ(x)：當x≠0時,δ(x)=0，但x=0時，δ(x)=∞。按20世紀前所形成的數學概念是無法理解這樣奇怪的函式的。然而物理學上一切點量，如點質量、點電荷、偶極子、瞬時打擊力、瞬時源等物理量用它來描述不僅方便、物理含義清楚,而且當它被當作普通函式參加運算,如對它進行微分和傅立葉變換，將它參與微分方程求解等所得到的數學結論和物理結論是吻合的。這就迫使人們要為這類怪函式確立嚴格的數學基礎。最初理解的方式之一是把這種怪函式構想成直線上某種分布所相應的“密度”函式。所以廣義函式又稱為分布，廣義函式論又叫做分布理論。用分布的觀念為這些怪函式建立基礎雖然很直觀，但對於複雜情況就又顯得繁瑣而不很明確。後來隨著泛函分析的發展，L.施瓦爾茨(1945)用泛函分析觀點為廣義函式建立了一整套嚴格的理論,接著И.□.蓋爾范德對廣義函式論又作了重要發展。

重要影響

J.（-S.）阿達馬(1932)在研究波動方程基本解時使用了發散積分的有限部分。С.Л.索伯列夫(1936)在研究雙曲型方程的柯西問題時用分部積分引入了廣義導數和微分方程廣義解的概念，並把函式δ及其導數δ□等視為某個函式空間上的線性泛函；他對廣義函式論的建立邁出了決定性的一步。S.博赫納(1932)和T.卡萊曼(1944)討論了冪增長函式的傅立葉變換，提出了連續函式的形式導數概念。

當然為那些怪函式建立嚴格數學基礎的方法並不是惟一的，例如波蘭學者J.米庫辛斯基就曾用較初等的方法建立它們的基礎。也有把廣義函式看作解析函式的邊界值，並由此發展出超函式理論。換句話說，廣義函式的定義並不完全統一，而是具有一定程度的靈活性，可以根據問題的需要適當地定出相應的廣義函式類。

基本函式空間和廣義函式空間

泛函分析觀念下的廣義函式理論的核心是把廣義函式看成某個函式空間上的連續線性泛函，即先選取某些性質很好的函式組成的線性空間，再在其中給出適當的收斂概念，這樣的函式空間就稱為基本函式空間，又稱為測試函式空間，而其中每個函式稱為基本函式或測試函式。相應於基個基本空間上的連續線性泛函就稱為該基本空間上的廣義函式。廣義函式全體就稱為相應於基本空間的廣義函式空間。常用的基本空間有□空間和□空間。