命名原因
泊松分布(Poissondistribution),台譯卜瓦松分布,是一種統計與機率學裡常見到的離散機率分布(discreteprobabilitydistribution)。泊松分布是以18~19世紀的法國數學家西莫恩·德尼·泊松(Siméon-DenisPoisson)命名的,他在1838年時發表。但是這個分布卻在更早些時候由貝努里家族的一個人描述過。就像當代科學史專家史蒂芬·施蒂格勒(StephenStigler)所說的誤稱定律(theLawofMisonomy),數學中根本沒有以其發明者命名的東西。分布特點
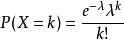 圖1
圖1泊松分布的期望和方差均為λ。
關係
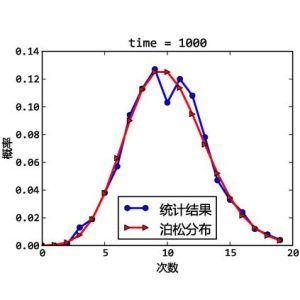
泊松分布與二項分布當二項分布的n很大而p很小時,泊松分布可作為二項分布的近似,其中λ為np。通常當n≧10,p≦0.1時,就可以用泊松公式近似得計算。
事實上,泊松分布正是由二項分布推導而來的,具體推導過程參見本詞條相關部分。
套用場景
在實際事例中,當一個隨機事件,例如某電話交換台收到的呼叫、來到某公共汽車站的乘客、某放射性物質發射出的粒子、顯微鏡下某區域中的白血球等等,以固定的平均瞬時速率λ(或稱密度)隨機且獨立地出現時,那么這個事件在單位時間(面積或體積)內出現的次數或個數就近似地服從泊松分布P(λ)。因此,泊松分布在管理科學、運籌學以及自然科學的某些問題中都占有重要的地位。套用示例
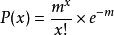 圖2
圖2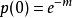 圖3
圖3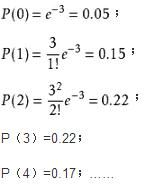 圖4
圖4P(0)是未產生二體的菌的存在機率,實際上其值的5%與採用0.05J/㎡照射時的大腸桿菌uvrA-株,recA-株(除去既不能修復又不能重組修復的二重突變)的生存率是一致的。由於該菌株每個基因組有一個二體就是致死量,因此P(1),P(2)……就意味著全部死亡的機率。
推導
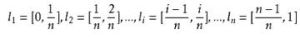 圖6
圖6為方便記,設所觀察的這段時間為[0,1),取一個很大的自然數n,把時間段[0,1)分為等長的n段:圖6。
我們做如下兩個假定:
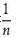 圖8
圖8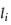 圖7
圖7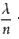 圖9
圖9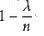 圖10
圖10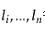 圖11
圖11 圖13
圖13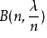 圖12
圖12