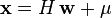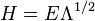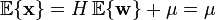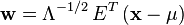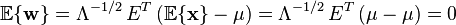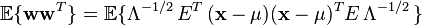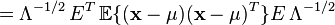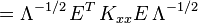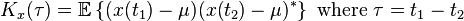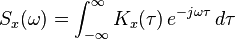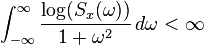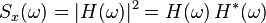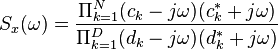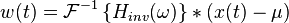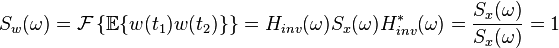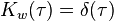技術定義
 白噪聲
白噪聲白噪聲的技術定義是:一種持續的噪聲,其在人類可聽見的頻率範圍內均勻分布。好比你是一個演奏者,彈出一個中央C音符,頻率是261.6赫茲。白噪聲就平均分布在人耳能聽到的從低到高的所有頻率上。還是用演奏音樂來比喻,這就像是一個超大的樂團一起演奏略有差異的音符。
理想的白噪聲具有無限頻寬,因而其能量是無限大,這在現實世界是不可能存在的。實際上,我們常常將有限頻寬的平整信號視為白噪聲,以方便進行數學分析。
統計特性
術語白噪聲也常用於表示在相關空間的自相關為0的空域噪聲信號,於是信號在空間頻率域內就是“白色”的,對於角頻率域內的信號也是這樣,例如夜空中向各個角度發散的信號。右面的圖片顯示了計算機產生的一個有限長度的離散時間白噪聲過程。
需要指出,相關性和機率分布是兩個不相關的概念。“白色”僅意味著信號是不相關的,白噪聲的定義除了要求均值為零外並沒有對信號應當服從哪種機率分布作出任何假設。因此,如果某白噪聲過程服從高斯分布,則它是“高斯白噪聲”。類似的,還有泊松白噪聲、柯西白噪聲等。人們經常將高斯白噪聲與白噪聲相混同,這是不正確的認識。根據中心極限定理,高斯白噪聲是許多現實世界過程的一個很好的近似,並且能夠生成數學上可以跟蹤的模型,這些模型用得如此頻繁以至於加性高斯白噪聲成了一個標準的縮寫詞:AWGN。此外,高斯白噪聲有著非常有用的統計學特性,因為高斯變數的獨立性與不相關性等價。
白噪聲是維納過程或者布朗運動的廣義均方導數(generalizedmean-squarederivative)。
白噪聲的數學期望為0:
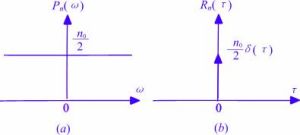
上式正是對白噪聲的“白色”性質在時域的描述。由於隨機過程的功率譜密度是其自相關函式的傅立葉變換,而δ函式的傅立葉變換為常數,因此白噪聲的功率譜密度是平坦的。
噪聲的顏色
噪聲的顏色分類來自於將頻域中的噪聲譜密度函式和頻域中的光波信號做形式上的類比,也就是說,如果一束光波在頻域內具有和藍噪聲相同的譜密度圖樣,則這束光波看上去將呈現藍色,以此類推。
最常用的有粉紅、棕色和藍色噪聲。
套用
白噪聲的套用領域之一是建築聲學,為了減弱內部空間中分散人注意力並且不希望出現的噪聲(如人的交談),使用持續的低強度噪聲作為背景聲音。一些緊急車輛的警報器也使用白噪聲,因為白噪聲能夠穿過如城市中交通噪聲這樣的背景噪聲並且不會引起反射,所以更加容易引起人們的注意。
在電子音樂中也有白噪聲的套用,它被直接或者作為濾波器的輸入信號以產生其它類型的噪聲信號,尤其是在音頻合成中,經常用來重現類似於鐃鈸這樣在頻域有很高噪聲成分的打擊樂器。
白噪聲也用來產生衝激回響。為了在一個演出地點保證音樂會或者其它演出的均衡效果,從PA系統發出一個瞬間的白噪聲或者粉紅噪聲,並且在不同的地方監測噪聲信號,這樣工程師就能夠建築物的聲學效應能夠自動地放大或者削減某些頻率,從而就可以調整總體的均衡效果以得到一個平衡的和聲。
白噪聲可以用於放大器或者電子濾波器的頻率回響測試,有時它與回響平坦的話筒或和自動均衡器一起使用。這個設計的思路是系統會產生白噪聲,話筒接收到揚聲器產生的白噪聲,然後在每個頻率段進行自動均衡從而得到一個平坦的回響。這種系統用在專業級的設備、高端的家庭立體聲系統或者一些高端的汽車收音機上。
白噪聲也作為一些隨機數字生成器的基礎使用。
白噪聲也可以用於審訊前使人迷惑,並且可能用於感覺剝奪技術的一部分。上市銷售的白噪聲機器產品有私密性增強器、睡眠輔助器以及掩飾耳鳴。
數學定義
白色隨機向量
一個隨機向量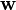 為一個白色隨機向量若且唯若它的平均值函式與自相關函式滿足以下條件:
為一個白色隨機向量若且唯若它的平均值函式與自相關函式滿足以下條件:
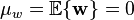

意即它是一個平均值為零的隨機向量,並且它的自相關函式是單位矩陣的倍數。
白色隨機過程(白噪聲)
一個時間連續隨機過程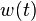 where
where  為一個白噪聲若且唯若它的平均值函式與自相關函式滿足以下條件:
為一個白噪聲若且唯若它的平均值函式與自相關函式滿足以下條件:
意即它是一個對所有時間其平均值為零的隨機過程,並且它的自相關函式是狄拉克δ函式,有無限大的功率。
由上述自相關函式可推出以下的功率譜密度。
由於δ函式的傅立葉變換為1。而對於所有頻率來說,此功率譜密度是一樣的。因此這是對白噪聲之“白色”性質在頻域的表述。
隨機向量變換
白色隨機向量的兩個理論套用是模擬以及whitening另外一個任意隨機向量。為了模擬一個任意隨機向量,我們使用一個仔細選擇的矩陣對白色隨機向量進行變換。我們選擇的變換矩陣能夠是被變換的白色隨機向量的平均值和協方差矩陣與模擬的任意向量的平均值和協方差矩陣相匹配。為了whiten一個任意的隨機向量,我們使用仔細選擇的矩陣對它進行變換,這樣得到的隨機向量就是一個白色隨機向量。
這兩個思想在通信和音頻領域中信道估計和信道均衡這樣的套用中是很關鍵的。這些思想在數據壓縮中也有套用。
模擬隨機向量
假設隨機向量 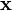 有協方差矩陣
有協方差矩陣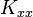 ,由於這個矩陣是共軛對稱和半正定,根據線性代數中的譜定理,我們可以用以下方法對角線或者分解矩陣,
,由於這個矩陣是共軛對稱和半正定,根據線性代數中的譜定理,我們可以用以下方法對角線或者分解矩陣,
通過對白色向量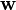 進行下面變換我們可以模擬這個平均為
進行下面變換我們可以模擬這個平均為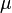 、協方差矩陣為
、協方差矩陣為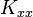 的隨機向量
的隨機向量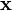 的一階和二階矩量屬性:
的一階和二階矩量屬性:
其中
這樣,這個變換輸出的期望是
協方差矩陣是
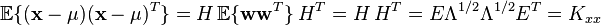
Whitening 隨機向量
whitening一個平均值為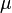 、協方差矩陣為
、協方差矩陣為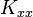 的向量
的向量 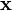 的方法是執行下面的計算:
的方法是執行下面的計算: 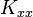 得到:
得到: 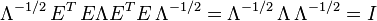
- 這樣,通過上面的變換就可以將隨機向量whiten成平均值為0、協方差矩陣是單位矩陣。
隨機信號變換
我們將模擬和白化這兩個概念推廣到連續時間隨機信號或者隨機過程。我們創建一個濾波器用於模擬,將白噪聲注入其中,用輸出信號模擬任意隨機過程的一階和二階矩。對於白化,我們將任意隨機信號注入所選濾波器中,濾波器輸出是白噪聲。模擬連續時間隨機信號
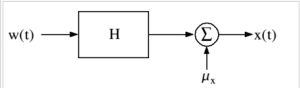 將白噪聲注入線性時不變濾波器中模擬任意隨機過程的一階和二階矩
將白噪聲注入線性時不變濾波器中模擬任意隨機過程的一階和二階矩 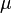 、協方差函式
、協方差函式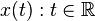
我們可以使用頻域技術模擬這個信號。
由於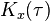 是個半正定的埃爾米特矩陣,所以
是個半正定的埃爾米特矩陣,所以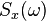 是實數並且若且唯若
是實數並且若且唯若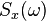 滿足Paley-Wiener criterion
滿足Paley-Wiener criterion
時可以factored為
選擇最小相位(minimumphase)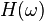 保證極點和零點都位於S面的左側,這樣我們就可以使用解析失敗(未知錯誤):
保證極點和零點都位於S面的左側,這樣我們就可以使用解析失敗(未知錯誤):
作為濾波器的傳遞函式來模擬 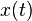 。
。
我們可以構建下面的線性、非時變 (time-invariant)濾波器來模擬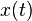
其中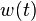 是有如下一階和二階矩屬性的連續時間的白噪聲:
是有如下一階和二階矩屬性的連續時間的白噪聲:
這樣,結果信號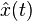 與所期望的信
與所期望的信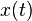 一樣有同樣的二階矩量屬性。
一樣有同樣的二階矩量屬性。
連續時間隨機信號的白化
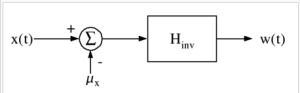 任意隨機過程 x(t) 輸入一個線性時不變濾波器,濾波器將 x(t)白化為白噪聲
任意隨機過程 x(t) 輸入一個線性時不變濾波器,濾波器將 x(t)白化為白噪聲 假設我們有一個廣義的穩定、連續時間隨機過程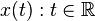 ,與上面定義的信號同樣的平均值
,與上面定義的信號同樣的平均值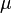 、協方差函式
、協方差函式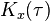 和功率譜密度
和功率譜密度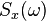 。
。
我們可以使用頻域技術白化這個信號,用上面的過程factor功率譜密度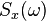 。
。
選擇最小相位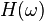 得到極點和零點都位於s面左側,這樣就可以用下面的inverse濾波器whiten
得到極點和零點都位於s面左側,這樣就可以用下面的inverse濾波器whiten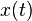
選擇的最小相位濾波器保證逆濾波器穩定的。另外,必須保證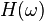 在所有
在所有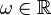 上都嚴格為正,這樣
上都嚴格為正,這樣 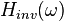 就不會有任何奇點。
就不會有任何奇點。
白化過程的最終格式如下所示:
相關研究
白噪聲有助睡眠
你在夜裡被吵醒,並不是說噪聲本身把你吵醒,而是噪聲的突然變化或突然停止刺激了你。白噪聲提供了一種屏障效應,禁止了那些會驚擾覺輕或是正在入睡的人的突然變化。神經科學家、《通感:聽力如何塑造大腦》一書作者塞斯·霍羅威茨說:“簡單而言就是,人在睡覺時聽覺仍在繼續工作。”史丹福大學人類睡眠研究中心主任克利特·櫛田稱:“這就是為什麼大多數人寧願聽著持續正壓通氣呼吸機發出的持續噪聲,也不願聽著他們伴侶高低起伏的鼾聲入睡。”
報導最後說,當然,並非所有人都需要聽著噪聲入睡。對於某些人來說,對大多數人有益的白噪聲恰恰會起到反作用,會使他們對背景聲音更敏感。

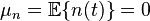
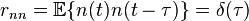
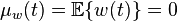
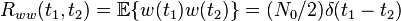
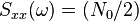
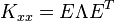
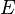 是
是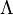 是
是