泰勒公式
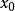 多項式近似
多項式近似在學習導數和微分概念時已知,如果函式f在 處可導,則有
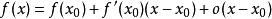 多項式近似
多項式近似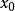 多項式近似
多項式近似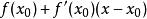 多項式近似
多項式近似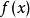 多項式近似
多項式近似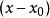 多項式近似
多項式近似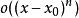 多項式近似
多項式近似即在點 附近,用一次多項式 逼近函式 ,其誤差為 的高階無窮小量。然而,在很多場合下,取一次多項式逼近是不夠的,往往需要二次或高於二次的多項式去逼近,並要求誤差為 ,其中,n為多項式的次數。
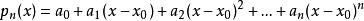 多項式近似
多項式近似為此,我們考察任一n次多項式
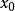 多項式近似
多項式近似逐次求它在點 處的導數,得到:
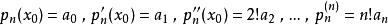 多項式近似
多項式近似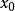 多項式近似
多項式近似對於一般函式f ,設它在點 存在直到n階的導數,由這些導數構造一個n次多項式
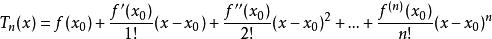 多項式近似
多項式近似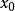 多項式近似
多項式近似稱為函式f在點 處的泰勒多項式
泰勒定理
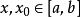 多項式近似
多項式近似 多項式近似
多項式近似若函式f 在[a,b]上存在直至n階的連續導數,在(a,b)記憶體在n+1階導函式,則對於任意給定的 ,至少存在一點 ,使得
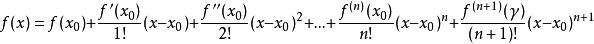 多項式近似
多項式近似麥克勞林公式
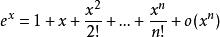 多項式近似
多項式近似(1)
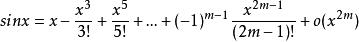 多項式近似
多項式近似(2)
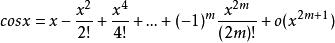 多項式近似
多項式近似(3)
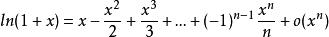 多項式近似
多項式近似(4)
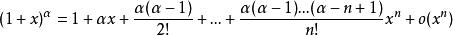 多項式近似
多項式近似(5)
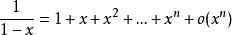 多項式近似
多項式近似(6)
近似計算
(示例)
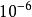 多項式近似
多項式近似計算 e 的值,使其誤差不超過 。
分析:
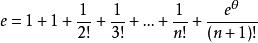 多項式近似
多項式近似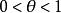 多項式近似
多項式近似其中,
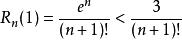 多項式近似
多項式近似故由
當n=9 時,便有
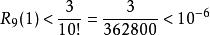 多項式近似
多項式近似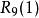 多項式近似
多項式近似從而略去 而求得e 得近似值為
 多項式近似
多項式近似