三角多項式

三角多項式是一類簡單的周期函式,但是，它是近似表示一般的周期函式的有效工具，隨著三角多項式的階的增高，任何連續的周期函式都可以藉助於三角多項逼近到預先給定的程度。三角多項式是在其他數學、物理、力學等領域中有著廣泛的套用。

三角多項式

正文

形如

的多項式，式中係數αk(k=0,1,…,n),bk(k=1,2,…,n)為任意給定的實數,αn,bn不全為零。n稱為此三角多項式的階數。任何一個三角多項式都是周期2π的周期函式,因此對於三角多項式的研究往往只要在長為2π的半開區間中進行。任何兩個三角多項式的和、差、積仍然是個三角多項式，而且,若Tn(r)與Tm(x)分別為n階與m階三角多項式，且m≥n，則Tn(x)±Tm(x)是個階不超過m的三角多項式,Tn(x)·Tm(x)是階為n+m的三角多項式。利用歐拉公式

,
，

任意一個n階三角多項式都可寫成

，

式中

n三角多項式在任一長為2π的半開區間中，最多只有2n個零點。因此,若兩個n階三角多項式在長為2π的半開區間中有2n+1個點處取值相同，則此兩個三角多項式完全相同。
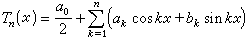
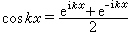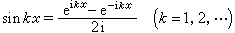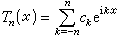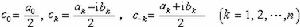
對於n階三角多項式Tn(x)，記

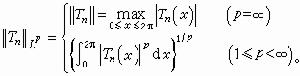
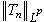常稱為Tn的Lp範數，若1≤p≤p┡≤∞，則

。

此外還有如下的尼科利斯基不等式

。

特別有

。

伯恩斯坦不等式　設Tn(x)是n階三角多項式,Tń(x)是它的導數，則有不等式

。

這是1912年С.Η.伯恩斯坦發現的，稱為伯恩斯坦不等式。其中係數n不能再減小，例如對任何常數A及α，Tn(x)=A sin(nx+α)都使它成等式。伯恩斯坦不等式在函式逼近論中起著重要的作用,並且有著各種拓廣。例如,С.Б.斯捷奇金於1948年證明,對任何n階三角多項式Tn(x)及自然數k，都有

，

式中 。
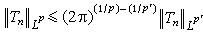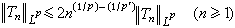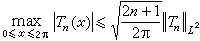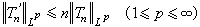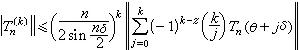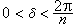共軛三角多項式　對給定的n階三角多項式Tn(x)，記

，

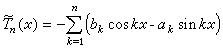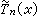稱為Tn(x)的共軛三角多項式。對於共軛三角多項式的導數有不等式

，

這裡係數n也是不能減小的。
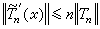應該指出,對於復係數三角多項式Tn(x)（即諸係數αk,bk為複數），同樣有

。

於是，對於自然數k，有

。

不僅如此，由此還能推出，若pn(z)是n次復係數代數多項式，則

。

關於n次代數多項式pn(x)，由伯恩斯坦不等式得到

。

此不等式在區間端點不合適，但有馬爾可夫不等式：

。

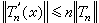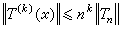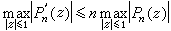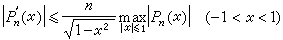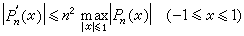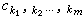多元三角多項式　設vj是自然數,zj是復變數(j=1,2,…,m),是僅與足碼有關的複數，則稱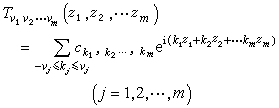

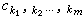為關於變數z1,z2,…,zm 的階分別為v1,v2,…,vm的三角多項式。如果係數滿足條件

，

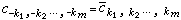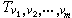則稱(z1,z2,…,zm)為實三角多項式。此時，如限制變數取實值，則它是一個實函式。實三角多項式也可以藉助歐拉公式將它改變為正弦函式與餘弦函式的實係數的多項式。例如，若Tυu(x，y)是關於變數x，y的vμ 階實三角多項式，則存在著僅與足碼有關的實數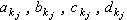，使得

實三角多項式與單變數的三角多項式有許多類似的地方，也可以建立種種不等式。
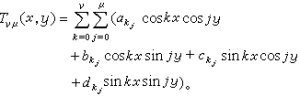
自然,三角多項式是一類簡單的周期函式,但是，它是近似表示一般的周期函式的有效工具，隨著三角多項式的階的增高，任何連續的周期函式都可以藉助於三角多項逼近到預先給定的程度。反之如果已知這種逼近程度的收斂於零的速度，也就有可能推出被逼近函式的構造性質,這個事實本身是有著深刻的物理意義的,周期運動的分解便是一個明顯的例證。三角多項式是在其他數學、物理、力學等領域中有著廣泛的套用。

配圖

相關連線