拉格朗日插值多項式逼近

拉格朗日插值多項式逼近

正文

拉格朗日插值多項式是一種最常見的多項式插值法，也是一種最常用的逼近工具。設ƒ(x)是定義在區間【α,b】上的函式，又設x1,x2,…,xn是【α,b】上的n個互不相同的點。早在1795年J.-L.拉格朗日就證明:如果在點xK處的函式值yK=ƒ(xK)(k=1,2,…,n)是已知的,則存在惟一的次數不高於n-1的代數多項式ln(ƒ,x)使得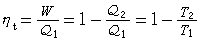

。

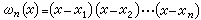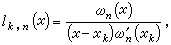
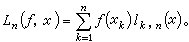
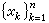倘若記

，

則ln(ƒ,x)有表達式

常稱ln(ƒ,x)為ƒ(x)的拉格朗日插值多項式，為其結點組。若ƒ(x)是個次數不高於n-1的代數多項式，則ln(ƒ,x)=ƒ(x)。ln(ƒ,x)的幾何意義是有且僅有一條n-1次代數曲線通過平面上預先給定的 n個橫坐標互不相同的點。又稱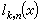為拉格朗日插值的基本多項式。不論在理論上還是在實用上，拉格朗日插值多項式都是一種重要的逼近工具。假設ƒ(x)在 【α,b】上存在n階導數，則ln(ƒ,x)逼近ƒ(x)的偏差有這樣的表達式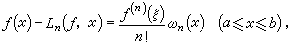

式中ξ是【α,b】中某一與x有關的點。當然，這裡對被逼近函式的要求太高，研究低度光滑函式的插值逼近是很重要的。
對於給定的結點組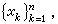記

常稱λn(x)為此結點組的勒貝格函式，λn為其勒貝格常數。如果記En-1(ƒ)為次數不高於n-1的代數多項式對連續函式ƒ(x)的最佳逼近值，則

而且有

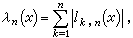
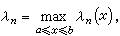
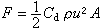
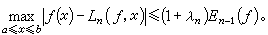
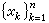因此，應該選取使λn儘可能小的結點組，或說讓諸結點在【α,b】上均勻分布是合理的。但事實並非這樣，即使對於函式ƒ(x)=｜2x-α-b｜,此時相應的ln(ƒ,x)也不能實現對ƒ(x)的逼近。至於選擇其他結點組,僅要求函式連續也未必可行。因為G.費伯曾經證明,對於【α,b】上的任意一列結點組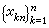，n =1，2，…,都有【α,b】上的連續函式ƒ(x)，使得相應的拉格朗日插值多項式序列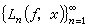在【α,b】上不一致收斂於ƒ(x)。此外,還有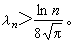

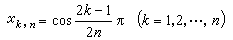
因此,選擇使勒貝格函式λn(x)關於 n的增長速度接近於ln n的結點組序列是人們所期望的。最常用的是在【-1,1】上取切比雪夫多項式Tn(x)=cos(n arccosx)的零點全體

作為結點組。
其相應的勒貝格常數不超過 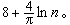於是只要函式ƒ(x)合乎迪尼－李普希茨條件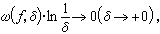則它的拉格朗日插值多項式ln(ƒ,x)在n →∞時，在【-1，1】上就一致收斂於ƒ(x)。這裡 ω(ƒ,δ)是ƒ(x)的連續性模。用這種結點組的拉格朗日插值多項式逼近連續函式，其逼近度與最佳逼近值相比較，還有一個對數因子。如何修改插值多項式的構造以改善它的逼近性能，是人們所重視的問題。修改的辦法很多，常用的是由С.Η.伯恩斯坦所提出的線性求和法。例如，令

x=cosθ (0≤θ≤π)，

定義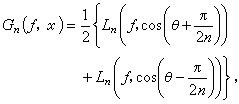

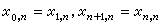或令，定義

如仍取Tn(x)的零點全體作為結點組,則存在絕對常數с，使得在［-1,1］上都有

這說明，上述兩種多項式對於低度光滑函式都有良好的逼近性能。
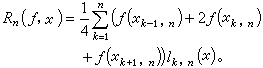
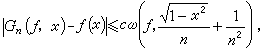
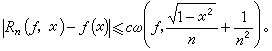
代替有限區間上的一致逼近，也可以考慮積分平均逼近，以及無限區間上的逼近。代替切比雪夫多項式的零點，可以考慮用雅可比多項式的零點作結點。而在周期的情況下，代替代數多項式的插值逼近自然以三角多項式的插值逼近為宜。此時，用周期區間的均勻分布的結點組是較合適的，可以建立類似於傅立葉級數部分和逼近函式的結果。

配圖

相關連線