簡介
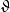 代數數域
代數數域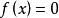 代數數域
代數數域命 為一個 n次代數數,即一個有理係數 n次不可約方程 的根。
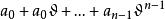 代數數域
代數數域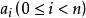 代數數域
代數數域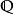 代數數域
代數數域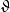 代數數域
代數數域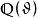 代數數域
代數數域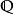 代數數域
代數數域 代數數域
代數數域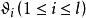 代數數域
代數數域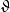 代數數域
代數數域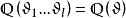 代數數域
代數數域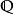 代數數域
代數數域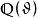 代數數域
代數數域易證所有形如 的數,此處 為有理數,所構成的集合,對和、差、積、商(除數非零)是自封的,所以構成一個域,這就是有理數域 添加 所得的單擴張(simple extension),常以 記之。可以證明對於 的任何有限擴張(finite extension) ,其中 都是代數數,均可找到一個代數數 使 。因此,只要考慮 的單擴張即可,稱 為一個代數數域。
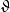 代數數域
代數數域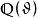 代數數域
代數數域所滿足的不可約方程的次數即定義為 的次數。
舉例
 代數數域
代數數域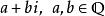 代數數域
代數數域最小最基本的代數數域是有理數域ℚ 。因為ℚ 自身是ℚ- 向量空間,維數是1。因此ℚ 是ℚ 自身的域擴張,。高斯有理數ℚ(i)(i為虛數單位)是數學家發現的第一個非平凡代數數域的例子,它是所有形同:的數構成的集合。
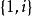 代數數域
代數數域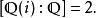 代數數域
代數數域可以證明,ℚ(i)是域,而且是ℚ-向量空間,以為基,空間維數是2。所以ℚ(i)是ℚ的二次擴張,。
 代數數域
代數數域 代數數域
代數數域 代數數域
代數數域 代數數域
代數數域給定不是完全平方數的正整數或相反數不是完全平方數的負整數 d ,二次域在ℚ中添加d的平方根而得的擴域。與高斯有理數域類似,可以證明是ℚ-向量空間,以為基,空間維數是2,即。
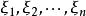 代數數域
代數數域 代數數域
代數數域考慮多項式方程 x =1 的 n 個復根,它們被稱做 n 次單位根,具體可以寫作:。
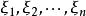 代數數域
代數數域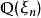 代數數域
代數數域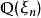 代數數域
代數數域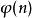 代數數域
代數數域 代數數域
代數數域在ℚ中添加得到的擴域稱為 n 次分圓域,記作。可以證明是有限維ℚ-向量空間,維數為(φ是數論中的歐拉函式),即。
實數域 ℝ 、複數域ℂ和 p 進數域ℚ都不是ℚ的有限擴張,因此都不是代數數域。任何有限域都不是ℚ的擴域,因此也不是代數數域。全體規矩數構成的域 和全體代數數構成的域 (有時也被簡稱為代數數域,與本文主題同名,但不是同一個概念)不是ℚ的有限擴張,因此都不是代數數域。
代數整數
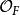 代數數域
代數數域代數整數是指能夠成為某個首一整數係數多項式的根的數。顯然代數整數是一種代數數。任何整數n都是一次整係數多項式X - n的根,因此是代數整數。給定代數數域F,F中所有代數整數構成一個環,稱作F中的(代數)整數環,也稱為F-整數環,記作。例如ℚ上的代數整數環就是 ℤ ,因此在代數數域研究中ℤ也被稱作“有理整數”(有理數域中的整數),以區別於其餘的代數整數。
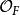 代數數域
代數數域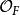 代數數域
代數數域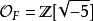 代數數域
代數數域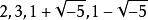 代數數域
代數數域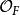 代數數域
代數數域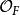 代數數域
代數數域 代數數域
代數數域代數數域F中的整數環與 ℤ 有不同的代數性質。不一定是唯一分解整環。舉例來說,設F=ℚ(−5),F中的整數環是。都是中的“素數”。正整數6,作為中的元素,它的素因數分解有兩種方式:
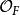 代數數域
代數數域有理整數的唯一分解性質在不少代數數域的整數環中失效。這個事實說明了拉梅對費馬大定理的證明是錯誤的。為此庫默爾等引進了理想數來作為彌補,由此發展出理想理論。代數數論中一個重要的事實是:的每個理想都可以唯一表示為素理想的乘積,即為戴德金整環。這種“理想的唯一素分解”可部分彌補“代數整數一般不能唯一素因子分解”的不足,在歷史上使代數數論發展起來。

