P 進數域
正文
又稱局部數域,它是數域關於p 進絕對值的完備化。p進數域的研究和代數數論的局部化方法,均始於K.亨澤爾1902年的工作。設p 是一個固定的素數,於是每個非零的有理整數α均可惟一地表成p 進位形式,即
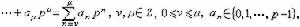
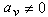 。如果定義
。如果定義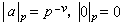 ,而對每個非零有理數α/b(α、b∈Z,b≠0),定義
,而對每個非零有理數α/b(α、b∈Z,b≠0),定義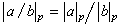 。函式
。函式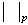 稱為Q 的p 進絕對值,它具有如下的性質:|α|p=0,若且唯若α=0;
稱為Q 的p 進絕對值,它具有如下的性質:|α|p=0,若且唯若α=0;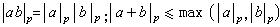 ,由此可知,
,由此可知,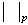 是Q 的非阿基米德絕對值,從而Q 關於由
是Q 的非阿基米德絕對值,從而Q 關於由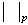 給出的拓撲,是一個豪斯多夫拓撲空間,但不是完備的。它的完備化就是p進數域,並記為Qp。 Qp中每個非零元素均可惟一表成
給出的拓撲,是一個豪斯多夫拓撲空間,但不是完備的。它的完備化就是p進數域,並記為Qp。 Qp中每個非零元素均可惟一表成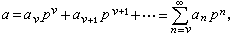
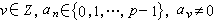 ,稱之為p 進數,而當v≥0時,稱之為p 進整數。全體p 進整數形成環,稱為p進整數環,記作Zp,即
,稱之為p 進數,而當v≥0時,稱之為p 進整數。全體p 進整數形成環,稱為p進整數環,記作Zp,即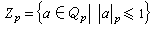 。環Zp有比較簡單的代數結構,例如,Zp 有惟一的素理想pZp=
。環Zp有比較簡單的代數結構,例如,Zp 有惟一的素理想pZp=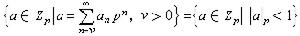 ,它也是Zp的惟一極大理想,而且(pZp)n=pnZp (n=0,1,2,…)構成環Zp的全部非零理想,從而Zp是主理想環,並且商環
,它也是Zp的惟一極大理想,而且(pZp)n=pnZp (n=0,1,2,…)構成環Zp的全部非零理想,從而Zp是主理想環,並且商環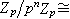
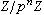 。特別地,Zp/pZp是p元域。Qp關於
。特別地,Zp/pZp是p元域。Qp關於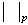 也有比較簡單的拓撲結構:Qp是完備的,每個理想
也有比較簡單的拓撲結構:Qp是完備的,每個理想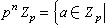
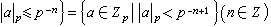 均是Qp中又開又閉的加法子群,並且它們形成0的基本鄰域組,從而Qp是全不連通的拓撲空間。因此,在研究Qp上的數論問題時較之於Q上有許多更好的工具。
均是Qp中又開又閉的加法子群,並且它們形成0的基本鄰域組,從而Qp是全不連通的拓撲空間。因此,在研究Qp上的數論問題時較之於Q上有許多更好的工具。 設K是任意代數數域,P為它的整數環OK中任一素理想。對每個非零元素
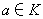 ,均有惟一的v∈Z,使得
,均有惟一的v∈Z,使得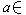
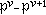 。定義
。定義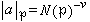 ,式中N(P)=|OK/P|(有限域OK/P的階數),而
,式中N(P)=|OK/P|(有限域OK/P的階數),而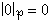 。於是函式||p也具有上述三性質。由此可知,||p是K 的一個非阿基米德絕對值,從而K 關於||p也是豪斯多夫拓撲空間,但不是完備的。它的完備化稱為p進數域(或局部數域),記作Kp。Kp中存在著N(P)-1個不同的N(P)-1次單位根。令S 是這些單位根和0 組成的集合,若取任意一個元素 π∈Kp,使得
。於是函式||p也具有上述三性質。由此可知,||p是K 的一個非阿基米德絕對值,從而K 關於||p也是豪斯多夫拓撲空間,但不是完備的。它的完備化稱為p進數域(或局部數域),記作Kp。Kp中存在著N(P)-1個不同的N(P)-1次單位根。令S 是這些單位根和0 組成的集合,若取任意一個元素 π∈Kp,使得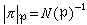 (可取P-P2中任一元素為π),則Kp中每個元素均可惟一表示成
(可取P-P2中任一元素為π),則Kp中每個元素均可惟一表示成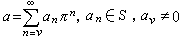 。當v≥0時,α稱為Kp中的整數,Kp中全體整數形成環Op,稱為Kp的整數環,於是
。當v≥0時,α稱為Kp中的整數,Kp中全體整數形成環Op,稱為Kp的整數環,於是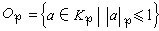 。Op有惟一的素理想
。Op有惟一的素理想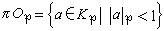 ,它也是Op的惟一極大理想,並且πnOp(n=0,1,2,…)構成Op的全部非零理想,從而Op也是主理想環。Op/πOp是N(P)元有限域,稱為Kp的剩餘類域,而S是此N(P)元域在Op中的一個完全代表系,稱為維特乘性代表系,π稱為域Kp的一個素元。每個域Kp也像Qp。那樣有比較簡單的代數結構和拓撲結構。
,它也是Op的惟一極大理想,並且πnOp(n=0,1,2,…)構成Op的全部非零理想,從而Op也是主理想環。Op/πOp是N(P)元有限域,稱為Kp的剩餘類域,而S是此N(P)元域在Op中的一個完全代表系,稱為維特乘性代表系,π稱為域Kp的一個素元。每個域Kp也像Qp。那樣有比較簡單的代數結構和拓撲結構。 局部數域Kp的有限次擴張仍是局部數域,於是有局部數域擴張的理論。局部數域有較簡單的代數結構和拓撲結構,而使得局部數域擴張理論較之於代數數域擴張理論要簡單。設l/K是局部數域的擴張,OK和OB分別是它們的整數環,P和B分別是OK和OB的惟一的極大理想,於是P在OB中生成的理想只能有形式Be,e稱為擴張l/K的分歧指數。另一方面,剩餘類域
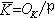 ,和
,和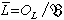 均是有限域,而且前者是後者的子域,其擴張次數
均是有限域,而且前者是後者的子域,其擴張次數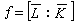 稱為擴張l/K的剩餘次數, 並有eƒ=【l:K】。每個局部數域擴張l/K 均有中間域M,使得M/K是ƒ次不分歧擴張,而l/M是e 次完全分歧擴張。此外,局部數域也有判別式,差積等概念和希爾伯特分歧理論,與代數數域擴張的情形很類似,但是要簡單得多。
稱為擴張l/K的剩餘次數, 並有eƒ=【l:K】。每個局部數域擴張l/K 均有中間域M,使得M/K是ƒ次不分歧擴張,而l/M是e 次完全分歧擴張。此外,局部數域也有判別式,差積等概念和希爾伯特分歧理論,與代數數域擴張的情形很類似,但是要簡單得多。 假設l/K是代數數域擴張,那么K中每個素理想P在l中有惟一的素因子分解式 PO,sub>L=
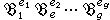 ,其中B1,B2,…Bg是l中不同的素理想。令ei和ƒi分別為Bi對於擴張l/K 的分歧指數和剩餘次數,則
,其中B1,B2,…Bg是l中不同的素理想。令ei和ƒi分別為Bi對於擴張l/K 的分歧指數和剩餘次數,則 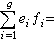 【l:K】。另一方面,局部數域l
【l:K】。另一方面,局部數域l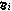 是Kp的擴域,並且
是Kp的擴域,並且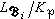 的分歧指數和剩餘次數恰好是ei和ƒi,因此,P在l中的分解情況可由諸局部數域擴張
的分歧指數和剩餘次數恰好是ei和ƒi,因此,P在l中的分解情況可由諸局部數域擴張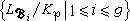 中的信息得到。此外,還有【l:K】=
中的信息得到。此外,還有【l:K】=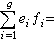
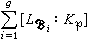 ,意即整體擴張次數是局部擴張諸次數之和。類似地還有l/K 的判別式是全體局部擴張判別式的乘積,等等。總之,局部數域擴張理論對於代數數域擴張理論這個代數數論的最基本課題的價值在於數域擴張l/K 的許多性質以某種方式是所有局部數域擴張lВ/Kp中類似性質的總和,這也是研究p進數域的主要意義。
,意即整體擴張次數是局部擴張諸次數之和。類似地還有l/K 的判別式是全體局部擴張判別式的乘積,等等。總之,局部數域擴張理論對於代數數域擴張理論這個代數數論的最基本課題的價值在於數域擴張l/K 的許多性質以某種方式是所有局部數域擴張lВ/Kp中類似性質的總和,這也是研究p進數域的主要意義。 1924年H.哈塞將這種思想成功地運用於二次型的研究之中。例如,設K 為代數數域,
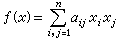 是域K上的二次型(即
是域K上的二次型(即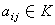 )。H.哈塞證明了,對於每個元素
)。H.哈塞證明了,對於每個元素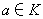 ,方程
,方程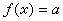 在K 中有解的充分必要條件是此方程在每個局部數域Kp(P過K的全部素理想,包括所謂“無限”素理想)中均有解。由於方程在Kp中的可解性有良好的判別法,將所有Kp的這些判別法匯集在一起,就得到代數數域中多元二次方程可解性的完整而切實可行的判別法。由於H.哈塞在二次型和其他問題上做了許多這類工作,後人就把體現這種思想的數學命題稱為哈塞的局部-整體原則。
在K 中有解的充分必要條件是此方程在每個局部數域Kp(P過K的全部素理想,包括所謂“無限”素理想)中均有解。由於方程在Kp中的可解性有良好的判別法,將所有Kp的這些判別法匯集在一起,就得到代數數域中多元二次方程可解性的完整而切實可行的判別法。由於H.哈塞在二次型和其他問題上做了許多這類工作,後人就把體現這種思想的數學命題稱為哈塞的局部-整體原則。 採用局部化方法(賦值論和Adèle、Idèle語言)能夠統一處理代數數域和以有限域為常數域的代數函式域。A.韋伊於1967年寫的《基礎數論》一書是這種方法的集中反映,對現代數論的發展有重要影響。
