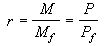概念
一個域上的n(n≥1)元有理函式域的有限擴張。設K是一個在任意域F上經添加有限個元素x1,…,xn,xn+1,…,xs所生成的域,其中x1,…,xn(n≥1)在F上是代數獨立的；xn+1,…,xs關於F(x1,…,xn)是代數元，則稱K是以F為係數域的n元代數函式域。當n=1時,簡稱K為F上的代數函式域,記作K/F。K中所有關於F的代數元成一個子域F┡，稱之為K/F的常量域。為了方便起見，以下設F本身就是K/F的常量域。介紹
除子 在代數函式域K/F中,K的一個不平凡賦值,若在F上是平凡的，則稱為K/F的一個賦值,由K/F的離散賦值所成的等價類,稱之為K/F的素除子。這種素除子有無限多個。作形式冪積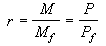
其中αp是整數,而且只有有限多個不為零;p取遍K/F 的所有素除子。這種α稱為K/F的除子。如果每個αp都不是負整數,那么α就稱為整除子。對於兩個除子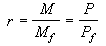和
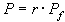規定:α=b，若且唯若對每個p都有αp=bp；規定乘法運算為 
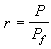；除子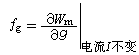
記為α-1。若α-1b是一整除子，則稱 α除盡b，記作α｜b。 虧格 由於素除子p的剩餘類域是F上的一個有限擴張,其擴張次數稱為素除子p的次數，記為d(p)。規定除子
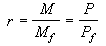的次數為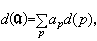
於是有d(α-1)=-d(α)以及d(αb)=d(α)+d(b)。 對於K中不為零的α,規範化的指數賦值vp（α）=mp是整數，且只有有限多個 p有 mp≠0，從而可作出除子
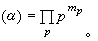設α是任一除子。子集L(α)=｛α∈K｜α=0，或者α|(α)｝形成F上的一個有限維空間,它的維數,記為l(α)。當α遍取K/F中所有的除子時,整數集{l(α)+d(α)}是有下界的。令
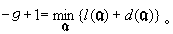由此確定的非負整數g是代數函式域的一個重要不變數，稱為K/F的虧格。雖然是B.黎曼首先明確提出並命名它為虧格的，但是早在N.H.阿貝爾的著作中就已經出現過。 微分和黎曼-羅赫定理 作K關於離散賦值vp的完備化(completion)Kp,於是Kp的元素都可以表作某個π∈K的形式冪級數。設F是個完全域(perfect field)。則可選擇適當的t∈K,使得K成為F(t)的可分代數擴張。另一方面,t作為Kp的元素,有
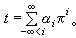規定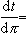
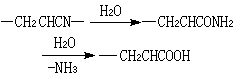並以dt記向量
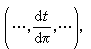其中每個分量是對不同的素除子p來取的,因此dt是個無限向量。對於K 中每個u,規定
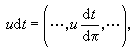並稱之為K的微分。當u≠0時，總有
於是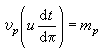
是整數，且只有有限多個不為零,由此定出一個除子
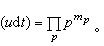若對某個除子b有b│(udt)，則稱udt被b除盡。K中所有被b除盡的微分（包括0）,組成F上一個有限維空間，它與t、π的選擇無關，它的維數記作δ(b)。 黎曼-羅赫定理 對於代數函式域K/F的任何一個除子α，恆有等式l(α)=d(α-1)-g+1+δ(α-1)成立。
虧格為0和1的代數函式域 F上的有理函式域F(x)，它的虧格為0。反之，若K/F的虧格是0,則除了有理函式域外，K只能是F上圓錐曲線的函式域，即K=F(x,y)，其中x與y滿足F上圓錐曲線的方程
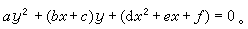
在歷史上曾企圖把形如
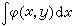的積分用有限的形式表出，於是引起對代數函式域的研究，這裡φ(x,y)是含x、y的有理式；y與x滿足一個整關係式ƒ(x,y)＝0。代數函式的理論,歷來就有幾種不同的描述方法,其中之一屬於“算術-代數”這一方向,即所謂代數函式域。它始於19世紀80年代R.戴德金和H.韋伯的工作。自20世紀以來,隨著抽象代數學的發展，戴德金和韋伯的理論,先後經E.諾特、 H.哈塞、F.K.施密特和 A.韋伊以及其他學者的逐步簡化和推廣,對域F的限制得以逐步解除，使這一理論的許多內容包括黎曼-羅赫定理，可以在F為任意域的情況下來建立。 參考書目
C.Chevalley,Introduction to the Theory of Algebraic functions of one variable, Amer. Math.Soc.,New York,1951.E.Artin,Algebraic Numbers and Algebraic Functions,Grodon and Breach,New York,1967.
