常見
常見的中心對稱圖形有:線段,矩形,菱形,正方形,平行四邊形,圓,邊數為偶數的正多邊形等。
例如:
正偶數邊形是中心對稱圖形正奇數邊形不是中心對稱圖形※正六角形是中心對稱圖形,等腰梯形不是中心對稱圖形,等邊三角形(正三角形)不是中心對稱圖形,反比例函式的圖像雙曲線是以原點為對稱中心的中心對稱圖形。
中心對稱的兩個圖形中的對應線段平行相等
國中定義
 中心對稱圖形
中心對稱圖形在平面內,把一個圖形繞著某個點鏇轉180°,如果鏇轉後的圖形能與原來的圖形重合,那么這個圖形叫做中心對稱圖形,這個點叫做它的對稱中心.
鏇轉前後圖形上能夠重合的點叫做對稱點.
1、理解中心對稱的定義要抓住以下三個要素:
(1)有一個對稱中心——點.
(2)圖形繞中心鏇轉180°.
(3)鏇轉後兩圖形重合.
2、中心對稱的性質
連線中心對稱圖形上每一對對稱點的線段都經過對稱中心,且被對稱中心平分.
3、中心對稱
在平面內,把一個圖形繞某一定點鏇轉180°,如果它能夠與另一個圖形重合,那么就說這兩個圖形關於這個點成中心對稱,這個點叫做對稱中心,鏇轉後兩個圖形上能夠重合的點叫做關於對稱中心的對稱點.
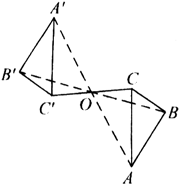
如圖,△ABC繞著點O鏇轉180°,和△A′B′C′能夠完全重合,則這兩個三角形關於點O對稱,點O叫對稱中心,A與A′,B與B′,C與C′叫關於O的對稱點.
 中心對稱圖形
中心對稱圖形注意:(1)中心對稱是指兩個圖形的關係,成中心對稱的兩個圖形只有一個對稱中心,並且一個圖形上的所有點關於對稱中心的對稱點都在另一個圖形上,反過來,另一個圖形上的所有點關於這箇中心的對稱點都在這個圖形上;
(2)中心對稱與中心對稱圖形之間的關係
區別:①中心對稱是指兩個圖形的關係,中心對稱圖形是指具有某種性質的圖形.
②成中心對稱的兩個圖形的對稱點分別在兩個圖形上,中心對稱圖形的對稱點在一個圖形上.
聯繫:若把中心對稱圖形的兩部分看成兩個圖形,則它們成中心對稱;若把中心對稱的兩個圖形看成一個整體,那么這個整體也就是中心對稱圖形.
4、中心對稱的特徵及識別方法
(1)關於中心對稱的兩個圖形,對稱點所連線段都經過對稱中心,而且被對稱中心所平分;
(2)關於中心對稱的兩個圖形是全等形;
(3)如果兩個圖形的對應點連成的線段都經過某一點,並且被該點平分,那么這兩個圖形關於這點成中心對稱;
(4)中心對稱的特徵揭示了其圖形的特徵. 如上圖所示,如果△ABC與△A′B′C′關於點O成中心對稱,則:①A,O,A′;B,O,B′;C,O,C′均三點共線,且OA=OA′,OB=OB′,OC=OC′;②△ABC≌△A′B′C′;
(5)如果已知△ABC與△A′B′C′關於某點成中心對稱,則點O必為AA′、BB′、CC′的中點,且它們是同一點,故也可以連結AA′、BB′,則其交點即為對稱中心.
5、關於原點對稱的點的坐標
兩個點關於原點對稱時,它們的坐標符號相反,即點P(x,y)關於原點的對稱點為P′(-x,-y).
理解關於原點對稱的點的坐標的特徵時,要結合圖形理解記憶,要善於將點的位置關係轉化為點的坐標的數量關係或將點的坐標的數量關係轉化為點的位置關係.
典型例題講解
例1、下列說法:
①成中心對稱的兩個圖形形狀一樣,大小一樣;
②成中心對稱的兩個圖形必須重合;
③形狀一樣,大小一樣的兩個圖形成中心對稱;
④鏇轉後能夠重合的兩個圖形成中心對稱.
其中說法正確的個數是(B)
A. 0個B. 1個C. 2個D. 3個
解析:
要注意能重合與必須重合,鏇轉與鏇轉180°的區別.由成中心對稱的性質知,成中心對稱的兩個圖形必定能重合,故①正確;成中心對稱的兩個圖形能重合,但是繞中心鏇轉180°後能重合,未鏇轉時它們不是必須重合,故②錯誤;形狀一樣,大小一樣的兩個圖形不一定處在成中心對稱的位置,由中心對稱的判定知,能重合的兩個圖形不一定成中心對稱,故③錯誤;成中心對稱的兩個圖形鏇轉後能重合,關鍵是要鏇轉180°後能重合,並非鏇轉任意角度就重合,故④錯誤.說法正確的個數只有1個,故選B.
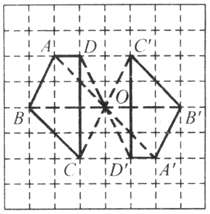
例2、如圖所示,請在格線中畫出四邊形A′B′C′D′,使它與原四邊形ABCD關於點O成中心對稱.
 中心對稱圖形
中心對稱圖形思路:
尋找A、B、C、D關於中心O的對稱點A′、B′、C′、D′,如A點對稱點畫法:①連結OA;②延長AO至A′,使OA′=OA,A′即為所求.
畫法:
(1)連結OA,並延長AO;
(2)在AO延長線上截取OA′=OA,得A的對稱點A′;(用刻度尺或圓規截取,不能估計)
(3)依次畫出B、C、D關於點O′的對稱點B′、C′、D′,連結A′B′,B′C′,C′D′,D′A′.
如圖所示,得四邊形A′B′C′D′為所求的四邊形.
總結:
(1)由中心對稱圖形性質:對應點與中心連線在一條直線上,並且被對稱中心平分,因此畫圖時,將A與O連結並延長一倍即可得到對應點A′;
(2)格線上對應點也可以通過數單位長度來確定對應點.
(3)一個圖形既軸對稱又中心對稱一定有兩條或兩條以上的對稱軸
正多邊形和圓
一、考點突破
1. 理解正多邊形和圓的有關概念;
2. 理解並掌握正多邊形半徑和邊長、邊心距、中心角之間的關係,能進行正多邊形的有關計算;
3. 通過等分圓周的方法,體會正多邊形與圓的關係,會套用正多邊形和圓的有關知識畫正多邊形。
二、重難點提示
重點:正多邊形半徑、中心角、邊心距、邊長之間的關係。
難點:理解正多邊形與圓的關係,利用正多邊形與圓的關係解決相關問題。
一、正多邊形的定義
各邊相等、各角也相等的多邊形叫做正多邊形,如正三角形(即等邊三角形)、正四邊形(即正方形)、正五邊形、正六邊形、正n邊形等。
二、正多邊形的有關概念
(1)正多邊形的中心:正多邊形的外接圓(或內切圓)的圓心。
(2)正多邊形的半徑:正多邊形外接圓的半徑。
(3) 正多邊形的邊心距:中心到正多邊形的一邊的距離(即正多邊形的內切圓的半徑)。
(4)正多邊形的中心角:正多邊形每一邊所對的圓心角.正多邊形的每一個中心角的度數是。
【核心突破】
(1)從圓的角度看:等分圓周可獲得正多邊形,把圓分成n(n≥3)等份。
①依次連線各分點所得的多邊形是這個圓的內接正n邊形。
②經過各分點作圓的切線,以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形。
(2)從正多邊形的角度看:任何正多邊形都有一個外接圓和一個內切圓,這兩個圓是同心圓。
【核心歸納】
一些特殊正多邊形的計算公式:
| 邊數n | 內角An | 中心角αn | 半徑R | 邊長an | 邊心距rn | 周長Pn | 面積Sn |
| 3 | 60° | 120° | R | R | R | 3R | R2 |
| 4 | 90° | 90° | R | R | R | 4R | 2R2 |
| 6 | 120° | 60° | R | R | R | 6R | R2 |
【重要提示】
正n邊形的對稱性:當n為奇數時,正n邊形只是軸對稱圖形;當n為偶數時,正n邊形既是軸對稱圖形,也是中心對稱圖形。
例題1如圖所示,在⊙O中,OA=AB,OC⊥AB,交⊙O於點C,那么下列結論錯誤的是()
A. ∠BAC=30°
B. 弧AC等於弧BC
C. 線段OB的長等於圓內接正六邊形的半徑
D. 弦AC的長等於圓內接正十二邊形的邊長
思路分析:根據正多邊形的性質和圓的相關概念對四個選項逐一進行分析。
答案:∵OA=OB,OA=AB,∴OA=BA=OB,∴△AOB是等邊三角形,∴∠AOB=60°,A. 根據圓周角定理得:∠BAC=∠BOC=∠BAO=×60°=15°,故本選項結論錯誤;B. ∵OC⊥AB,OC為半徑,∴弧AC=弧BC,故本選項結論正確;C. ∵△ABO為等邊三角形,∠AOB=60°,以AB為一邊可構成正六邊形,故本選項結論正確;D. 因為OC⊥AB,根據垂徑定理可知,弧AC=弧BC,再根據A中結論,弦AC的長等於圓內接正十二邊形的邊長,故本選項結論正確;故選A。
技巧點撥:本題主要考查正多邊形和圓的計算問題,屬於常規題,要注意圓周角定理的套用。
例題2如圖所示,已知正五邊形ABCDE,AF∥CD交DB的延長線於點F,交DE的延長線於點G。
(1)寫出圖中所有的等腰三角形;
(2)求證:∠G=2∠F。
思路分析:(1)利用等腰三角形的性質以及正五邊形的性質得出各角度進而得出答案;
(2)先求∠G與∠F的度數,再得出它們之間的關係。
答案:(1)∵DC=BC,∴△CDB是等腰三角形,∵∠C=108°,∴∠1=∠CBD=36°,∵AF∥CD,∴∠F=∠1=36°,可得四邊形DEAB是等腰梯形,∴∠DBA=∠2=72°,∴∠F=∠BAF=36°,∴△BAF是等腰三角形,進而可得:∠GEA=∠G=∠2=72°,∴△FDG,△AEG是等腰三角形,故等腰三角形有:△BCD,△ABF,△FDG,△AEG。
(2)由(1)可知∠F=36°,∠G=72°,故∠G=2∠F。
技巧點撥:本題主要考查了等腰三角形的性質與判定以及正五邊形的性質等知識,得出各角度數是解題關鍵。
例題3某學習小組在探索“各內角都相等的圓內接多邊形是否為正多邊形”時,有如下探討:
甲同學:我發現這種多邊形不一定是正多邊形,如圓內接矩形不一定是正方形。
乙同學:我知道,邊數為3時,它是正三角形;我想,邊數為5時,它可能也是正五邊形……
丙同學:我發現邊數為6時,它也不一定是正六邊形。如圖2所示,△ABC是正三角形,弧AD、弧BE、弧CF均相等,這樣構造的六邊形ADBECF不是正六邊形。
(1)如圖1,若圓內接五邊形ABCDE的各內角均相等,則∠ABC=__________,請簡要說明圓內接五邊形ABCDE為正五邊形的理由。
(2)如圖2,請證明丙同學構造的六邊形各內角相等。
(3)根據以上探索過程,就問題“各內角都相等的圓內接多邊形是否為正多邊形”的結論與“邊數n(n≥3,n為整數)”的關係,提出你的猜想(不需證明)。
思路分析:(1)先根據多邊形內角和定理求出正五邊形的內角和,再求出各角的度數;根據各角度數證明各邊之間的關係即可;(2)由圖知∠AFC對,由=,而∠DAF對的=+=+=,故可得出∠AFC=∠DAF,同理可證其餘各角都等於∠AFC,由此即可得出結論;(3)根據(1)、(2)的證明即可得出結論。
答案:(1)∵五邊形的內角和=(5-2)×180°=540°,∴∠ABC==108°,理由:∵∠A=∠B=∠C=∠D=∠E,∠A對著,∠B對著,∴=,∴-=-,即=,∴BC=AE,同理可證其餘各邊都相等,∴五邊形ABCDE是正五邊形。
(2)由圖知∠AFC對,而∠DAF對,∵=,∴+=+,即=,∴∠AFC=∠DAF.同理可證其餘各角都等於∠AFC,故圖2中六邊形各角相等。
(3)由(1)、(2)可知,當n(n≥3,n為整數)是奇數時,各內角都相等的圓內接多邊形是正多邊形;當n(n≥3,n為整數)是偶數時,各內角都相等的圓內接多邊形不一定為正多邊形。
技巧點撥:本題考查的是正多邊形和圓,熟知弧、圓心角、弦的關係是解答本題的關鍵。
【方法提煉】
1. 求中心角的常用方法:正n邊形的中心角為,與正n邊形的一個外角相等,與正n邊形的一個內角互補。
2. 正多邊形的外接圓半徑R與邊長a、邊心距r之間的關係式為R2=r2+(a)2,這是把正n邊形分成了2n個全等的直角三角形,把正n邊形的有關計算轉化為直角三角形中的問題。
滿分訓練:
例:正多邊形的一個外角等於45°,那么這個正多邊形的內角和等於__________,中心角是__________。
解:n×45°=360°,∴n=8。由內角和公式得(8-2)·180°=1080°,∴中心角為=45°。
(答題時間:30分鐘)
1. 如圖,邊長為a的正六邊形內有兩個三角形(數據如圖),則=( )
A. 3B. 4C. 5D. 6
2. 閱讀理解:如圖1,在平面內選一定點O,引一條有方向的射線Ox,再選定一個單位長度,那么平面上任一點M的位置可由∠MOx的度數θ與OM的長度m確定,有序數對(θ,m)稱為M點的“極坐標”,這樣建立的坐標系稱為“極坐標系”。套用:在圖2的極坐標系下,如果正六邊形的邊長為2,有一邊OA在射線Ox上,則正六邊形的頂點C的極坐標應記為( )
A. (60°,4)B. (45°,4)C. (60°,2)D. (50°,2)
*3. 用摺紙的方法,可直接剪出一個正五邊形(如圖所示)。方法是:拿一張長方形紙對摺,摺痕為AB,以AB的中點O為頂點將平角五等分,並沿五等分的線摺疊,再沿CD剪開,使展開後的圖形為正五邊形,則∠OCD等於( )
A. 108°B. 90°C. 72°D. 60°
4. 如圖,若干全等正五邊形排成環狀。圖中所示的是前3個五邊形,要完成這一圓環還需__________個五邊形。
**5. 如圖,在正八邊形ABCDEFGH中,四邊形BCFG的面積為20cm2,則正八邊形的面積為__________cm2。
6. 在學習圓與正多邊形時,馬露、高靜兩位同學設計了一個畫圓內接正三角形的方法:
(1)如圖,作直徑AD;
(2)作半徑OD的垂直平分線,交⊙O於B,C兩點;
(3)連線AB、AC、BC,那么△ABC為所求的三角形。
請你判斷兩位同學的做法是否正確,如果正確,請你按照兩位同學設計的畫法,畫出△ABC,然後給出△ABC是等邊三角形的證明過程;如果不正確,請說明理由。
*7. 如圖(1)、(2)、(3)、…、(n),M、N分別是⊙O的內接正三角形ABC、正方形ABCD、正五邊形ABCDE、…、正n邊形ABCDE…的邊AB、BC上的點,且BM=CN,連線OM、ON。
(1)求圖(1)中∠MON的度數;
(2)圖(2)中∠MON的度數是__________,圖(3)中∠MON的度數是__________;
(3)試探究∠MON的度數與正n邊形邊數n的關係(直接寫出答案)。
1. C 解析:如圖,顯然圖中兩個空白直角三角形全等,把兩個空白三角形拼成一個邊長為a的等邊三角形,而正六邊形可分成六個如△AOB一樣邊長為a的等邊三角形,所以==5。
2. A 解析:如圖,設正六邊形的中心為D,連線AD,∵∠ADO=360°÷6=60°,OD=AD,∴△AOD是等邊三角形,∴OD=OA=2,∠AOD=60°,∴OC=2OD=2×2=4,∴正六邊形的頂點C的極坐標應記為(60°,4)。故選A。
*3. B 解析:這裡的O點是所剪正五邊形的中心,由題可知∠COD=36°,所以剪得的三角形正好是五邊形一邊和兩條半徑所構成的三角形的一半,所以∠OCD=90°。
4. 7 解析:延長正五邊形的相鄰兩邊,交於圓心,∵正五邊形的外角等於360°÷5=72°,∴延長正五邊形的相鄰兩邊圍成的角的度數為:180°-72°-72°=36°,∴360°÷36°=10,
∴排成圓環需要10個正五邊形,故還需7個五邊形。
**5. 40 解析:連線HE,AD,在正八邊形ABCDEFGH中,可得:HE⊥BG於點M,AD⊥BG於點N,∵正八邊形每個內角為:=135°,∴∠HGM=45°,∴MH=MG,設MH=MG=x,則HG=AH=AB=GF=x,∴BG×GF=2(+1)x2=20,四邊形ABGH面積=(AH+BG)×HM=(+1)x2=10,∴正八邊形的面積為:10×2+20=40(cm2)。
6. 解:兩位同學的方法正確。連線BO、CO,∵BC垂直平分OD,∴直角△OEB中,OE=OB,∴∠BOE=60°,由垂徑定理得∠COE=∠BOE=60°,由於AD為直徑,∴∠AOB=∠AOC=120°,∴AB=BC=CA,即△ABC為等邊三角形。
*7. 解:(1)連線OB、OC,∵正△ABC內接於⊙O,∴∠OBM=∠OCN=30°,∠BOC=120°,又∵BM=CN,OB=OC,∴△OBM≌△OCN,∴∠BOM=∠CON,∴∠MON=∠BOC=120°;(2)圖(2)中,∠MON==90°,圖(3)中,∠MON==72°;(3)圖(n)中,∠MON=。

