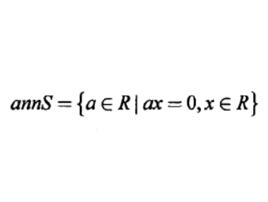定義
定義一
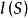 零化子
零化子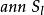 零化子
零化子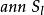 零化子
零化子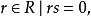 零化子
零化子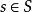 零化子
零化子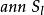 零化子
零化子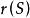 零化子
零化子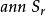 零化子
零化子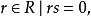 零化子
零化子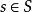 零化子
零化子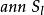 零化子
零化子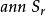 零化子
零化子設S是環R的子集,R中一切左乘S中每一個元都等於零的元素的集合,稱為S的左零化子,通常記為或,即={對任意}。是R的一個左理想。同樣地,S在R中的右零化子=={對任意}是R的右理想,∩稱為S在R中的零化子,它是R的理想。
定義二
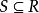 零化子
零化子假定R是環,S是R的非空子集合, ,那么
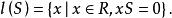 零化子
零化子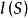 零化子
零化子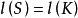 零化子
零化子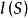 零化子
零化子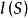 零化子
零化子叫做R中S的左零化子或簡稱R中左零化子或左零化子,顯然 是R的左理想,假如K是由S生成的R的右理想,那么,因此我們也可以假定S是R的右理想,這樣 就是R的右理想S的左零化子,如果S是左理想或理想,那么 就是理想。
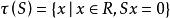 零化子
零化子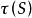 零化子
零化子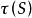 零化子
零化子同樣 叫做R中S的右零化子或R中右零化子或右零化子,顯然 是R的右理想,我們也可把看成R的左理想S的右零化子,右理想的右零化子或理想的右零化子都是理想。
R的理想如果又是R中左零化子或右零化子,就叫做R的零化理想,顯然R自身是R中的零化理想,假如環R有單位元或是半質環,那么O是R的零化理想。
零化子的性質
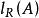 零化子
零化子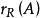 零化子
零化子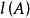 零化子
零化子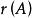 零化子
零化子把 和 分別簡記為 和。
1 引理
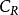 零化子
零化子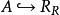 零化子
零化子設 是餘生成子,則對於每個 有:
 零化子
零化子2 定理
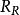 零化子
零化子若 是內射的,則有
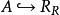 零化子
零化子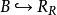 零化子
零化子(1)對任意 ,,有
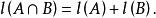 零化子
零化子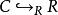 零化子
零化子(2)對任意有限生成的 有
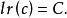 零化子
零化子3 定理
如果定理2中的條件(1),(2)成立,則任意從R的有限生成右理想到R的同態可由R的某個元素左乘得到。
4 推論
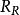 零化子
零化子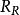 零化子
零化子若 是Noether的且定理2中的條件(1),(2)成立,則 是內射的。
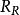 零化子
零化子證明:因為是Noether的,所以R的每個右理想是有限生成的,於是由定理3和Baer判別定理就得到命題。