定義
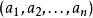 最大公因子
最大公因子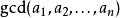 最大公因子
最大公因子最大公因子,又稱最大公約數(英語:greatest common divisor,gcd),指兩個或多個整數共同具有的最大約數,記為 或 。
求兩個整數最大公約數主要的方法:
•窮舉法:分別列出兩整數的所有約數,並找出最大的公約數。
•素因數分解:分別列出兩數的素因數分解式,並計算共同項的乘積。
•短除法:兩數除以其公同素因數,直到兩數互素時,所有除數的乘積即為最大公約數。
•輾轉相除法:兩數相除,取餘數重複進行相除,直到餘數為{\displaystyle 0}時,前一個除數即為最大公約數。
兩個整數{\displaystyle a,b}的最大公約數和最低公倍數(lcm)的關係為:
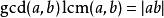 最大公因子
最大公因子兩個整數的最大公約數可用於計算兩數的最低公倍數,或分數化簡成最簡分數。
兩個整數的最大公約數和最低公倍數中存在分配律:
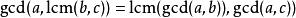 最大公因子
最大公因子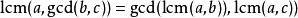 最大公因子
最大公因子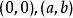 最大公因子
最大公因子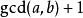 最大公因子
最大公因子在直角坐標中,兩頂點為 的線段會通過 個格子點。
例子
54可以表示為兩兩不同正整數的乘積:
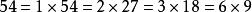 最大公因子
最大公因子 最大公因子
最大公因子故54的正約數為 。
同樣地,24可以表示為:
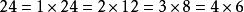 最大公因子
最大公因子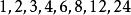 最大公因子
最大公因子故24的正約數為 。
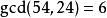 最大公因子
最大公因子24,54都有的正約數1,2,3,6即為 公約數,其中最大的公約數6即為 最大公約數,記為 。
程式代碼
數字之間的最大公約數之所有約數是該組數字所有的公約數。
以下使用輾轉相除法實現。
C#
1 private int GCD(int a, int b){
2 if(0 != b) while(0 != (a %= b) && 0 != (b %= a));
3 return a + b;
4 }
C++
運行時計算實現:
template < typename T >
T GCD(T a, T b)
{ if(b) while((a %= b) && (b %= a));
return a + b;}
編譯時計算實現:
#include <iostream>
#include <type_traits>
template<typename T, std::enable_if_t<std::is_integral<T>::value, T> a, std::enable_if_t<std::is_integral<T>::value, T> b>
struct HCF{
public:
static const T value=HCF<T, (a>b? b: a), (a>b? a%b: b%a)>::value;
};
template<typename T, std::enable_if_t<std::is_integral<T>::value, T> a>
struct HCF<T, a, 0>{
public:
static const T value=a;
};
int main(){ std::wcout<<HCF<int, 12, 64>::value<<std::endl;//Output: 4}
C
int GCD(int a, int b) {
if(b) while((a %= b) && (b %= a));
return a + b;}
Java
private int GCD(int a, int b){
if(b==0) return a; return a % b == 0 ? b : GCD(b, a % b);}
Python
GCD = lambda a, b: (GCD(b, a % b) if a % b else b)
