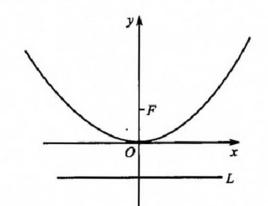
定義
拋物線定義:平面內與一個定點 F 和一條直線 l 的距離相等的點的軌跡叫做拋物線,點 F 叫做拋物線的焦點,直線 l 叫做拋物線的準線,定點 F不在定直線上。它與橢圓、雙曲線的第二定義相仿,僅比值(離心率 e)不同,當 e=1時為拋物線,當0<e<1時為橢圓,當e>1時為雙曲線。
方程
拋物線的標準方程有四種形式,參數 p的幾何意義,是焦點到準線的距離,掌握不同形式方程的幾何性質(如下表):其中P(x0,y0)為拋物線上任一點。
| 標準方程 | y^2=2px(p>0) | y^2=-2px(p>0) | x^2 =2p y(p>0) | x^2 =-2p y(p>0) |
| 圖形 | 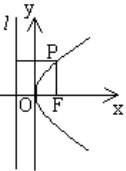 拋物線方程 拋物線方程 | 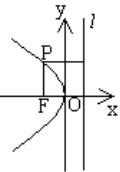 拋物線方程 拋物線方程 | 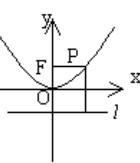 拋物線方程 拋物線方程 | 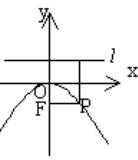 拋物線方程 拋物線方程 |
| 範圍 | x≥ 0, y 拋物線方程 拋物線方程 | x≤ 0, y 拋物線方程 拋物線方程 | y≥ 0, x 拋物線方程 拋物線方程 | y≤ 0, x 拋物線方程 拋物線方程 |
| 對稱軸 | X軸 | y軸 | ||
| 頂點坐標 | 原點O(0,0) | |||
| 焦點坐標 | (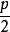 拋物線方程 拋物線方程 | (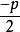 拋物線方程 拋物線方程 | (0,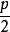 拋物線方程 拋物線方程 | (0,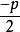 拋物線方程 拋物線方程 |
| 準線方程 | 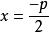 拋物線方程 拋物線方程 | 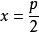 拋物線方程 拋物線方程 | 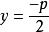 拋物線方程 拋物線方程 | 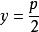 拋物線方程 拋物線方程 |
| 離心率 | e = 1 | |||
| 焦半徑 | 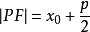 拋物線方程 拋物線方程 | 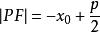 拋物線方程 拋物線方程 | 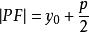 拋物線方程 拋物線方程 | 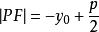 拋物線方程 拋物線方程 |
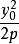 拋物線方程
拋物線方程對於拋物線y^2=2px(p≠0)上的點的坐標可設為(,y),以簡化運算。
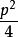 拋物線方程
拋物線方程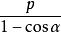 拋物線方程
拋物線方程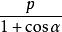 拋物線方程
拋物線方程拋物線的焦點弦:設過拋物線y^2=2px(p>0)的焦點F的直線與拋物線交於A(x,y)、B(x,y),直線OA與OB的斜率分別為k,k,直線l的傾斜角為α,則有yy=-p^2,xx=,kk=-4,|OA|=,|OB|=,|AB|=x+x+p
幾何性質
方程的具體表達式為y=ax^2+bx+c
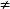 拋物線方程
拋物線方程⑴a 0
⑵a>0,則拋物線開口朝上;a<0,則拋物線開口朝下;
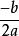 拋物線方程
拋物線方程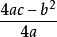 拋物線方程
拋物線方程⑶極值點(頂點):(,);
⑷Δ=b^2-4ac,
Δ>0,圖象與x軸交於兩點:
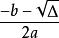 拋物線方程
拋物線方程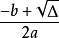 拋物線方程
拋物線方程(,0)和(,0);
Δ=0,圖象與x軸交於一點:
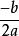 拋物線方程
拋物線方程(,0);
Δ<0,圖象與x軸無交點;
若拋物線交y軸為正半軸,則c>0。若拋物線交y軸為負半軸,則c<0。