基本介紹
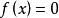 拋物線法
拋物線法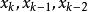 拋物線法
拋物線法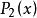 拋物線法
拋物線法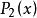 拋物線法
拋物線法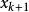 拋物線法
拋物線法設方程 的3個近似根為 ,我們以這三點為節點構造二次插值多項式 ,並適當選取 的1個零點 作為新的近似根,這樣確定的疊代過程稱為 拋物線法,也稱為 密勒(Miller)法。
幾何意義
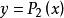 拋物線法
拋物線法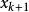 拋物線法
拋物線法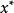 拋物線法
拋物線法在幾何圖形上,這種方法的基本思想是用拋物線 與x軸的交點 作為所求根 的新近似根(圖1)。
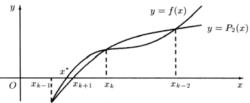 圖1
圖1計算公式推導
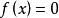 拋物線法
拋物線法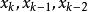 拋物線法
拋物線法現在推導拋物線法的計算公式,用方程 的近似根 作插值多項式
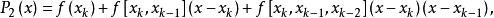 拋物線法
拋物線法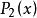 拋物線法
拋物線法則 有兩個零點
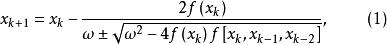 拋物線法
拋物線法式中
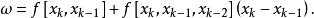 拋物線法
拋物線法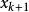 拋物線法
拋物線法為了從式(1)定出1個值 ,我們需要討論根式前正負號的取捨問題。
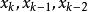 拋物線法
拋物線法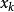 拋物線法
拋物線法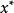 拋物線法
拋物線法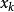 拋物線法
拋物線法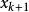 拋物線法
拋物線法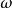 拋物線法
拋物線法在 3個近似根中,自然假定 更接近所求的根 ,這時,為了保證精度,我們選式(1)中較接近 的1個值作為新的近似根 。為此,只要取根式前的符號與 的符號相同即可。
拋物線法的收斂定理
關於拋物線法有如下收斂定理。
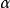 拋物線法
拋物線法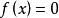 拋物線法
拋物線法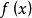 拋物線法
拋物線法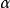 拋物線法
拋物線法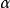 拋物線法
拋物線法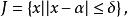 拋物線法
拋物線法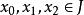 拋物線法
拋物線法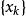 拋物線法
拋物線法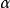 拋物線法
拋物線法定理1 設為方程的單重根,的三階導數在根的鄰域裡連續,則存在的一個適當小的鄰域當時,由拋物線法產生的序列收斂於,且有
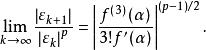 拋物線法
拋物線法例題解析
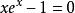 拋物線法
拋物線法用拋物線法求解方程 。
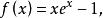 拋物線法
拋物線法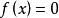 拋物線法
拋物線法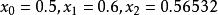 拋物線法
拋物線法解: 設 選取方程 的3個近似根 作為初始值,計算得
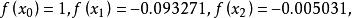 拋物線法
拋物線法故
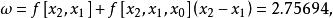 拋物線法
拋物線法從而由式(1)可得
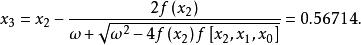 拋物線法
拋物線法
