定義
形式冪級數是一個數學中的抽象概念,是從冪級數中抽離出來的代數對象。形式冪級數和從多項式中剝離出來的多項式環類似,不過允許(可數)無窮多項因子相加,但不像冪級數一般要求研究是否收斂和是否有確定的取值。形式冪級數在代數和組合理論中有廣泛套用。
 形式冪級數
形式冪級數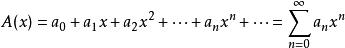 形式冪級數
形式冪級數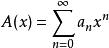 形式冪級數
形式冪級數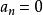 形式冪級數
形式冪級數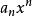 形式冪級數
形式冪級數設x是一個符號, 為實數,則 稱為以x為未定元的一個形式冪級數。約定:如果在形式冪級數 中某個 ,則 可略去。
在形式冪級數中,x從來不指定一個數值,且對收斂和發散的問題不感興趣,感興趣的是係數序列(a(0),a(1),...,a(n),...),我們研究形式冪級數完全可以歸結為討論這些係數序列,且這些係數序列又可看作含有分量a(0),a(1),...,a(n),...的無窮矢量,係數a(0)稱為級數的常數係數。
運算
我們把形式冪級數看做是收斂的並在其上作代數運算。
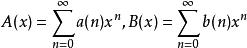 形式冪級數
形式冪級數已知兩個形式冪級數 ,則兩級數之間可進行如下運算:
相等
若對所有的n>0,有a(n)=b(n),則稱兩形式冪級數相等,有A(x)=B(x)。
和
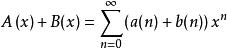 形式冪級數
形式冪級數兩形式冪級數的和定義為: 。兩形式冪級數的和運算滿足交換律和結合律。
乘積
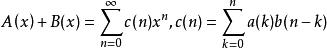 形式冪級數
形式冪級數兩形式冪級數的乘積定義為: ,稱序列{c(n)}為序列{a(n)}與序列{b(n)}的柯西乘積。兩形式冪級數的乘積運算對加法滿足分配律。
逆元
定義
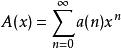 形式冪級數
形式冪級數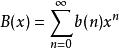 形式冪級數
形式冪級數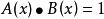 形式冪級數
形式冪級數設有形式冪級數,若存在形式冪級數,使得,則稱B(t)是A(t)的一個逆元。
定理
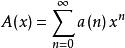 形式冪級數
形式冪級數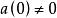 形式冪級數
形式冪級數形式冪級數有逆元的充分必要條件是,且若A(x)有逆元,則逆元必唯一。
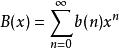 形式冪級數
形式冪級數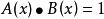 形式冪級數
形式冪級數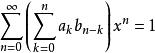 形式冪級數
形式冪級數證明:設A(x)有逆元,因為,所以,從而對任何一個自然數n,有:
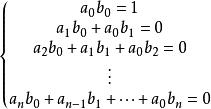 形式冪級數
形式冪級數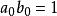 形式冪級數
形式冪級數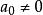 形式冪級數
形式冪級數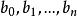 形式冪級數
形式冪級數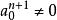 形式冪級數
形式冪級數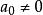 形式冪級數
形式冪級數因為,所以,把看成未知數,則上述方程組的係數行列式的值。由克萊姆法則可知,若A(x)有逆元,則且逆元唯一。
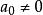 形式冪級數
形式冪級數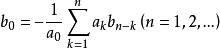 形式冪級數
形式冪級數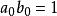 形式冪級數
形式冪級數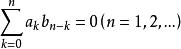 形式冪級數
形式冪級數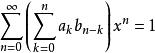 形式冪級數
形式冪級數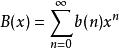 形式冪級數
形式冪級數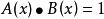 形式冪級數
形式冪級數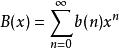 形式冪級數
形式冪級數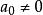 形式冪級數
形式冪級數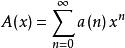 形式冪級數
形式冪級數反之,設,令,則,且,於是,令,則,故是A(x)的逆元,也就是說當時,有逆元。

