定義
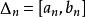 區間套
區間套 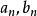 區間套
區間套 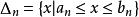 區間套
區間套 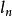 區間套
區間套 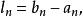 區間套
區間套 設表示以為端點的閉區間,即,而用記其長度,即假若它們滿足以下兩個條件:
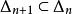 區間套
區間套 1)對所有的n,皆有;
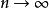 區間套
區間套 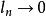 區間套
區間套 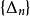 區間套
區間套 2)當時,,那么,就稱是一個 區間套。
區間套定理
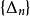 區間套
區間套 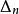 區間套
區間套 若是一個區間套,則存在唯一的實數c屬於所有的區間。
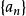 區間套
區間套 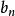 區間套
區間套 證明: 由區間套的條件1)易知:數列是單調遞增的,且有界(任一皆為其上界),故必有極限,令
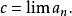 區間套
區間套 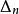 區間套
區間套 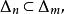 區間套
區間套 現證數c屬於一切區間,為此,取某個固定的自然m,則對大於m的n,皆有故知
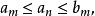 區間套
區間套 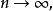 區間套
區間套 現令則有
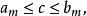 區間套
區間套 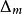 區間套
區間套 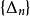 區間套
區間套 即數c屬於區間,因m是任意,故c屬於區間套的所有區間。
最後再證 唯一性、為此,該用反證法;
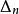 區間套
區間套 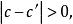 區間套
區間套 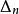 區間套
區間套 假定c‘是屬於一切區間的另一數,那么因為它們都屬於,故有
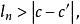 區間套
區間套 於是有
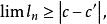 區間套
區間套 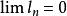 區間套
區間套 這與區間套的條件2)是矛盾的,故知屬於所有區間的c是唯一的。
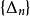 區間套
區間套 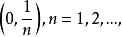 區間套
區間套 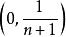 區間套
區間套 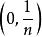 區間套
區間套 應該強調的是:區間套中的區間,必需是閉的(包含二端點在內),否則,區間套定理就未必成立.譬如,取一系列不包含端點的開區間容易看出:包含在之中,且有
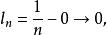 區間套
區間套 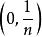 區間套
區間套 但卻不存在任何實數屬於所有的區間。
詳細介紹
 區間套
區間套 我們怎樣描述一個無理實數呢?對於像這樣一些數,我們能夠給出簡單的幾何表征,但這並不總是容易做到的,足以產生每一個實數點的一種通用可行的方法,乃是通過越來越精確的有理近似值數列來描述數值x,特別是,我們將從左、右兩邊同時逼近x,其精確度逐次增高,而使得誤差的界限趨向於零,換句話說,我們採用這樣一個包含x的端點為有理數的區間“序列”,其中每一個區間都包含著下一個區間,而且使得此序列中充分靠後的那些區間,其區間的長度,隨同其近似值的誤差,小於任何預先指定的正數。
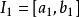 區間套
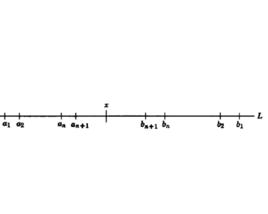
區間套 首先,設x含於閉區間之中,即
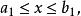 區間套
區間套  圖1 區間套序列
圖1 區間套序列  區間套
區間套 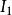 區間套
區間套 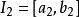 區間套
區間套 這裡都是有理數(見圖1),在之中,我們考慮一個包含x的“子區間”,即
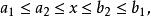 區間套
區間套  區間套
區間套  區間套
區間套  區間套
區間套 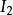 區間套
區間套 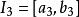 區間套
區間套 這裡都是有理數,例如,我們可以取的某一半作為,因為x必定處在區間的這一半或那一半之中。在之中,我們也考慮包含x的子區間,
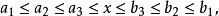 區間套
區間套 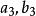 區間套
區間套 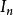 區間套
區間套 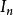 區間套
區間套 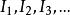 區間套
區間套 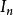 區間套
區間套 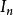 區間套
區間套 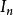 區間套
區間套 這裡都是有理數,如此等等,我們要求區間的長度隨n增加而趨向於零;即對於所有足夠大的n,的長度小於任何預先指定的正數,一個閉區間的集合,其中每一個都包含著下一個並且其長度趨向於零,我們稱它為“ 區間套序列”。點x由區間套序列唯一確定,即沒有另一點y能夠處於所有之中,因為,只要n足夠大,x和y之間的距離就會超過的長度,由於這裡我們總是選取有理點作為的端點,又因為具有有理端點的每一個區間由兩個有理數來描述,於是我們看到, L上的每一個點,即每一個實數,能夠由無窮多個有理數來準確地描述,逆命題並不是顯而易見的;我們將把它當作一個基本公理來接受。
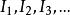 區間套
區間套 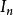 區間套
區間套 區間套公理:如果是一個具有有理端點的區間套序列,則存在一個點x包含於所有的之中。這是一個連續性公理:這個公理保證實軸上沒有空隙存在。