發展史
發展內容
 初等代數
初等代數在高等代數中,一次方程組(即線性方程組)發展成為線性代數理論;而二次以上方程發展成為多項式理論。前者是向量空間、線性變換、型論、不變數論和張量代數等內容的一門近世代數分支學科,而後者是研究只含有一個未知量的任意次方程的一門近世代數分支學科。作為大學課程的高等代數,只研究它們的基礎。高次方程組(即非線性方程組)發展成為一門比較現代的數學理論-代數幾何。
線性代數是高等代數的一大分支。我們知道一次方程叫做線性方程,討論線性方程及線性運算的代數就叫做線性代數。線上性代數中最重要的內容就是行列式和矩陣。行列式和矩陣在十九世紀受到很大的注意,而且寫了成千篇關於這兩個課題的文章。向量的概念,從數學的觀點來看不過是有序三元數組的一個集合,然而它以力或速度作為直接的物理意義,並且數學上用它能立刻寫出物理上所說的事情。向量用於梯度,散度,鏇度就更有說服力。同樣,行列式和矩陣如導數一樣(雖然‘dy/dx’在數學上不過是一個符號,表示包括‘Δy/Δx’的極限的長式子,但導數本身是一個強有力的概念,能使我們直接而創造性地想像物理上發生的事情)。因此,雖然表面上看,行列式和矩陣不過是一種語言或速記,但它的大多數生動的概念能對新的思想領域提供鑰匙。然而已經證明這兩個概念是數學物理上高度有用的工具。
線性代數學科和矩陣理論是伴隨著線性系統方程係數研究而引入和發展的。
發展初期
十七世紀日本數學家關孝和提出了行列式(determinant)的概念,他在1683年寫了一部叫做《解伏題之法》的著作,意思是“解行列式問題的方法”,書里對行列式的概念和它的展開已經有了清楚的敘述。而在歐洲,第一個提出行列式概念的是德國的數學家,微積分學奠基人之一萊布尼茲(Leibnitz,1693年)。
1750年克萊姆(Cramer)在他的《線性代數分析導言》(Introduction d l'analyse des lignes courbes alge'briques)中發表了求解線性系統方程的重要基本公式(既人們熟悉的Cramer克萊姆法則)。
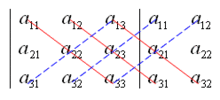 三階行列式展開的沙路法則
三階行列式展開的沙路法則1764年,Bezout把確定行列式每一項的符號的手續系統化了。對給定了含n個未知量的n個齊次線性方程,Bezout證明了係數行列式等於零是這方程組有非零解的條件。Vandermonde是第一個對行列式理論進行系統的闡述(即把行列式理論與線性方程組求解相分離)的人。並且給出了一條法則,用二階子式和它們的餘子式來展開行列式。就對行列式本身進行研究這一點而言,他是這門理論的奠基人。
 拉格朗日
拉格朗日參照克萊姆和Bezout的工作,1772年,Laplace在《對積分和世界體系的探討》中,證明了Vandermonde的一些規則,並推廣了他的展開行列式的方法,用r行中所含的子式和它們的餘子式的集合來展開行列式,這個方法如今仍然以他的名字命名。1841年,德國數學家雅可比(Jacobi)總結並提出了行列式的最系統的理論。另一個研究行列式的是法國最偉大的數學家柯西(Cauchy),他大大發展了行列式的理論,在行列式的記號中他把元素排成方陣並首次採用了雙重足標的新記法,與此同時發現兩行列式相乘的公式及改進並證明了laplace的展開定理。相對而言,最早利用矩陣概念的是拉格朗日(Lagrange)在1700年後的雙線性型工作中體現的。拉格朗日期望了解多元函式的最大、最小值問題,其方法就是人們知道的拉格朗日疊代法。為了完成這些,他首先需要一階偏導數為0,另外還要有二階偏導數矩陣的條件。這個條件就是今天所謂的正、負的定義。儘管拉格朗日沒有明確地提出利用矩陣。
大約在1800年,高斯(Gauss)提出了高斯消元法並用它解決了天體計算和後來的地球表面測量計算中的最小二乘法問題。(這種涉及測量、求取地球形狀或當地精確位置的套用數學分支稱為測地學。)雖然高斯由於這個技術成功地消去了線性方程的變數而出名,但早在幾世紀中國人的手稿中就出現了解釋如何運用“高斯”消去的方法求解帶有三個未知量的三方程系統。在當時的幾年裡,高斯消去法一直被認為是測地學發展的一部分,而不是數學。而高斯- 約當消去法則最初是出現在由Wilhelm Jordan撰寫的測地學手冊中。許多人把著名的數學家Camille Jordan誤認為是“高斯- 約當”消去法中的約當。
矩陣代數的豐富發展,人們需要有合適的符號和合適的矩陣乘法定義。二者要在大約同一時間和同一地點相遇。
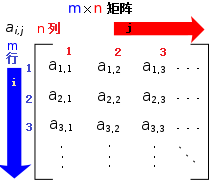 矩陣
矩陣1848年,英格蘭的J.J. Sylvester首先提出了矩陣(matrix)這個詞,它來源於拉丁語,代表一排數。在1855年矩陣代數得到了Arthur Cayley的進一步發展。Cayley研究了線性變換的組成並提出了矩陣乘法的定義,使得複合變換ST的係數矩陣變為矩陣S和矩陣T的乘積。他還進一步研究了那些包括矩陣的逆在內的代數問題。1858年,Cayley在他的矩陣理論文集中提出著名的Cayley-Hamilton理論,即斷言一個矩陣的平方就是它的特徵多項式的根。利用單一的字母A來表示矩陣是對矩陣代數發展至關重要的。在發展的早期公式
det(AB)=det(A)det(B)為矩陣代數和行列式間提供了一種聯繫。數學家Cauchy首先給出了特徵方程的術語,並證明了階數超過3的矩陣有特徵值及任意階實對稱行列式都有實特徵值;給出了相似矩陣的概念,並證明了相似矩陣有相同的特徵值;研究了代換理論。
數學家試圖研究向量代數,但在任意維數中並沒有兩個向量乘積的自然定義。第一個涉及一個不可交換向量積(既V×W不等於W×V)的向量代數是由Hermann Grassmann在他的《線性擴張論》(Die lineale Ausdehnungslehre)一書中提出的(1844)。他的觀點還被引入一個列矩陣和一個行矩陣的乘積中,結果就是現在稱之為秩數為1的矩陣,或簡單矩陣。在19世紀末美國數學物理學家吉布斯(Willard Gibbs)發表了關於《向量分析基礎》(Elements of Vector Analysis)的著名論述。其後物理學家狄拉克(P.A.M. Dirac)提出了行向量和列向量的乘積為標量。我們習慣的列矩陣和向量都是在20世紀由物理學家給出的。
矩陣的發展是與線性變換密切相連的。到19世紀它還僅占線性變換理論形成中有限的空間。現代向量空間的定義是由Peano於1888年提出的。
生活運用
二次世界大戰後隨著現代數字計算機的發展,矩陣又有了新的含義,特別是在矩陣的數值分析等方面。由於計算機的飛速發展和廣泛套用,許多實際問題可以通過離散化的數值計算得到定量的解決。於是作為處理離散問題的線性代數,成為從事科學研究和工程設計的科技人員必備的數學基礎。
關係區別
很多人把高等代數和線性代數混為一談,但其實高等代數是大學數學專業開設的專業課,線性代數是大學中除了數學專業以外的理科,工科和部分醫科專業開設的課程。
代數學、幾何學、分析數學是數學的三大基礎學科,數學的各個分支的發生和發展,基本上都是圍繞著這三大學科進行的。
代數學與另兩門學科的區別,主要在以下兩點:
首先,代數運算是有限次的,而且缺乏連續性的概念。也就是說,代數學主要是關於離散性的。儘管在現實中連續性和不連續性是辯證的統一的,但是為了認識現實,有時候需要把它分成幾個部分,然後分別地研究認識,再綜合起來,就得到對現實的總的認識。這是我們認識事物的簡單但是科學的重要手段,也是代數學的基本思想和方法。代數學注意到離散關係,並不能說明這時它的缺點,時間已經多次、多方位的證明了代數學的這一特點是有效的。
其次,代數學除了對物理、化學等科學有直接的實踐意義外,就數學本身來說,代數學也占有重要的地位。代數學中發生的許多新的思想和概念,大大地豐富了數學的許多分支,成為眾多學科的共同基礎。
清華大學出版社出版圖書
 高等代數
高等代數作者:陳小松、李俊平、劉金旺、劉慶平、王國富
圖書詳細信息
ISBN:9787302370963
定價:35元
印次:1-1
裝幀:平裝
印刷日期:2014-9-2
圖書簡介:
本書是為高等院校數學類專業編寫的高等代數教材。包含多項式、行列式、線性方程組、矩陣、二次型、向量空間、線性變換、歐氏空間,雙線性函式共9章內容。在注重強化基礎知識及其訓練的同時,兼顧套用以及與數學軟體的結合,內容精煉,重點突出。每章最後一節也可以作為學生自主研學的內容,對培養學生主動學習的能力大有益處。
前言
高等代數所包含的教學內容在大學數學專業、理科和工科專業都起著重要的作用.在教與學的過程中教材起著重要的作用. 一本好的教材,我們認為要具有以下五個條件:一是要注意繼承過去已列名優教材的優點,教學內容選擇要恰當,內容安排順序要自然,循序漸進,由淺入深;二是要注重教學內容的歷史,問題的目的、來源和發展要簡單扼要地交待清楚,強化“問題驅動”的教學思想;三是要與時俱進,注重教學內容的套用,要將數學套用和數學軟體融入到教材里,注重將數學軟體的套用編入到例題和習題中,可以作為學生自主研學的輔助材料;四是要適合專業的特點,要給教師根據教學對象和學時多少選擇教學內容的餘地,教材要包含大多數名優教材的基本內容,以便於教師和學生查閱;五是要以學生為中心,充分發揮學生的主體作用,將引導學生進行自主研究性學習內容選入教材. 我們根據多年的教學經驗和體會,編寫了這本教材.我們注意繼承過去名優教材的優點,同時具有如下特點:第一,注重了教學內容的歷史;第二,注重了教學內容的套用;第三,注重了將數學軟體Maple套用到習題中,可以作為學生自主研學的輔助素材;第四,我們也將習題單獨裝訂為合頁冊,方便學生習題和交作業,也方便老師批改;第五,部分調整了教學體系的結構,使得教學內容由淺入深,注重啟發性,避免教學內容單純重複;第六,增加了中英文對照的名詞索引.
李俊平教授、劉金旺教授、劉慶平教授、王國富副教授和我多次對該教材進行討論、編寫和修改,並為本套教材配備了習題. 教材由劉偉俊教授審稿. 該書適合數學、信息與計算科學及統計學專業作為教材使用,也適合一些理科專業的學生對其內容選擇使用. 可以根據課程的學時,適當選擇教學內容. 例如,教學計畫為128學時的,可以選擇除9.3節,9.4節以外的所有內容,教學計畫為88學時的,可以選擇1.1~1.4節,第2章到第6章中非星號部分加上7.1~7.8節、8.1~8.6節的內容.整個教材中打星號的部分,可供教師教學時選擇. 每一章的最後一節可以作為學生自主研學、開展科研訓練的內容. 教材可能還會存在一些問題,希望使用該教材的同學和老師將問題指出來,傳送到我的信箱,以便今後重印或再版時修改.
陳小松
2014年5月於中南大學
目錄
第1章多項式
1.1數域整數的整除性
1.2一元多項式
1.3整除的概念
1.4最大公因式
1.5因式分解
1.6重因式
1.7多項式函式
1.8復係數與實係數多項式
1.9有理數域上多項式
1.10多元多項式
1.11對稱多項式
*1.12套用和利用Maple計算舉例
第1章習題
第2章行列式
2.1行列式的引入
2.2排列
2.3n級行列式
2.4行列式的性質
2.5克萊姆法則
*2.6拉普拉斯定理和行列式乘法法則
*2.7套用和利用Maple計算舉例
第2章習題
第3章線性方程組
3.1線性方程組的消元法
3.2n維向量空間
3.3矩陣的秩
3.4線性方程組有解的判定法
3.5線性方程組解的結構
*3.6二元高次方程組
*3.7套用和利用Maple計算舉例
第3章習題
第4章矩陣
4.1矩陣的運算
4.2矩陣乘積的行列式與矩陣的逆
4.3矩陣的分塊初等矩陣
4.4矩陣的分塊舉例
*4.5套用和利用Maple計算舉例
第4章習題
第5章二次型
5.1二次型的矩陣表示
5.2標準形
5.3複數域和實數域上的二次型
5.4正定二次型
*5.5套用和利用Maple計算舉例
第5章習題
第6章向量空間
6.1向量空間的定義與簡單性質
6.2向量的線性相關性
6.3向量空間的基坐標
6.4基變換與坐標變換
6.5子空間
6.6子空間的交與和
6.7子空間的直和
6.8線性映射向量空間的同構
*6.9套用和利用Maple計算舉例
第6章習題
第7章線性變換
7.1線性變換
7.2線性變換的運算
7.3線性變換的矩陣
7.4特徵值與特徵向量
7.5對角矩陣
7.6線性變換的像與核
7.7不變子空間
7.8若爾當標準形
7.9λ矩陣的概念不變因子
7.10行列式因子初等因子
7.11矩陣相似的條件
7.12初等因子和標準形
*7.13套用和利用Maple計算舉例
第7章習題
第8章歐氏空間
8.1定義和性質
8.2正交組標準正交基
8.3同構
8.4正交變換
8.5正交補向量到子空間的距離
8.6對稱變換實對稱矩陣的標準形
8.7酉空間介紹
*8.8套用和利用Maple計算舉例
第8章習題
第9章雙線性函式
9.1線性函式
9.2雙線性函式
*9.3辛空間
*9.4對偶空間
*9.5雙線性函式的套用
第9章習題
附錄Maple簡介
索引

