集合論公理系統
正文
公理集合論的基礎部分。如同平面幾何中的點、線、面一樣，集合是一個不加定義的原始概念。集合和屬於關係∈是通過公理刻畫的。例如，“任一集合由它的元素所惟一決定”是通過外延公理刻畫的。“存在一無窮集合”是無窮公理所斷定的。集合的運算（如無序對、並、冪等）也是通過公理加以刻畫和保證的。雖然每一公理都不是藉助於直觀(因為直觀不嚴謹可能發生錯誤)而是藉助於嚴謹的形式語言加以刻畫的，然而公理的背景都是很深刻和很直觀的，它們來源於G.（F.P.）康托爾的樸素集合論，是從他的理論中抽象出來的基本原則。因此，每一公理都是刻畫集合或類的某一基本性質。把某些公理蒐集在一起組成刻畫集合或類的特徵的若干基本原則，就稱為集合論的一個公理系統。具體地說，在康托爾集合論中包含著深刻的、豐富的、新型的推理方法。悖論的發現促使人們藉助於公理化方法，以期排除集合論中的已知悖論並系統地整理G.康托爾的理論和方法。1908年出現兩個著名的公理系統，這就是E.F.F.策梅洛的系統和B.A.W.羅素的類型論。之後，集合論公理系統的研究成了一個重要的方向和領域。除了對上述兩個系統的擴充、加工和修改之外，還出現了一些新的系統,其中最著名的是J.馮·諾伊曼1925年提出的系統,後經P.貝爾奈斯、K.哥德爾修改形成的GB系統，人們通常把這個系統記作NBG或GB。除了上述三個最著名的系統外，還有奎因系統，王浩系統，阿克曼系統，莫利和斯科特系統也都是值得重視的。近年來,人們也相當重視非直謂類的公理系統,其中有本質上是貝爾奈斯1961年給出的BC系統。
策梅洛-弗倫克爾公理系統 在1908年策梅洛系統的基礎上，經A.T.斯科朗、A.A.弗倫克爾的改進與補充而建立的一個公理系統，是康托爾集合論方法的形式化處理。它易於理解，是影響最廣的一個系統，人們通常把上述系統叫做ZF系統，並簡記為ZF。它的原始概念是集合和屬於關係，它們不是由定義給出的，而是藉助於一階語言（見一階邏輯）由公理直接予以刻畫的。這一系統的公理是下述10條。
① 外延公理 對於任意的兩個集合x與y，如果x的任一元都是y的元，反之,y的任一元都是x的元,則x＝y。換句話說,對於任意兩個集合,它們的元素相同時，它們為同一個集合,亦即
。 ② 空集合存在公理 存在一個沒有任何元素的集合。也就是說,空集合是存在的,空集合通常記作
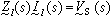。即彐x凬y(y唘x)。 ③ 無序對集合存在公理 對於任意的集合x，y,都存在一集合z，它的元素恰好是x 與y ，即
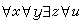
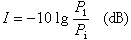。此公理中的集合z，記作{x,y},稱為x與y的無序對集合。當x=y時,它就是{x},此時稱｛x｝為x的單元集合。 ④ 並集合公理 對於任意的集合x，都存在一集合y，y的元素恰好是x的所有元素的元素，即
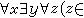
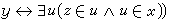。此公理中定義的集合y 稱為x的並集合，記作∪x。由此公理,對於任意的集合S1,S2，它們的並S1∪S2就定義為集合∪{S1,S2}。 ⑤ 冪集合公理 對於任意的集合x,都有一個集合y，y的元素恰好是x的子集合。即
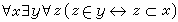，其中
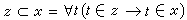。此公理中定義的集合 y稱為x的冪集合，記作P(x)。 ⑥ 無窮公理 存在著一個集合,它的元素恰好是所有自然數，此集合記作ω。即
。
。
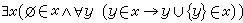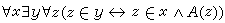⑧ 替換公理模式 對於任意的公式A(x,y),如果對任意的集合x，都有惟一的集合y，使得A(x,y)成立，那么對任意的集合S1，有一集合S2，使得S2 ={u｜t∈S1且A(t,u)}。也就是說,若A(x,y)具有一對一的性質，這時，對於任一集合S1,由S1中每一元素經A(x,y)對應的值組成一集合，即
。
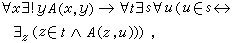
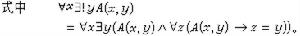
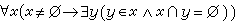在策梅洛1908年的論文中，分離公理中的A(z)僅指集合的性質。然而，性質仍然是一個很含混的概念，弗倫克爾把性質形式化為一階語言中的公式，從而使這一概念清晰和嚴謹了。在文獻中，人們常把公理①～⑦與⑨～⑩一起記為Z（即策梅洛系統）,把公理①～⑩一起記為ZF。有時為了突出選擇公理，人們也把公理①～⑨記為ZF，而把公理①～⑩記為ZFC。
ZF的獨立性問題 ZF不是獨立的，例如，由公理①～⑥與⑧～⑨可以推出公理⑦。但由於公理⑦是策梅洛首先提出的，具有歷史意義，並且運用方便，由它來證明交、笛卡兒乘積等運算的合法性都是相當簡潔的。因此，一般說來，公理⑦還是給予保留的。
ZF的完備性問題 皮亞諾算術公理都是ZF的定理，它們都可以直接從ZF推得。因此，由哥德爾不完備性定理可知，ZF是不完備的。
ZF的協調性問題 據哥德爾第二不完備性定理，ZF的協調性只能在比它可強的系統中證明。例如,在ZF+大基礎公理（即“存在一大基數”）的公理系統中，可以證明ZF是協調的。
類型論 關於集合的型的層次理論。它包括兩部分的內容:簡單類型論和分支類型論。在簡單類型論中,每一集合都有一確定的層次。一集合x能夠是另一集合y的元素，若且唯若y的層次比x的層次恰好多一,層次為0的對象是本元（或稱為個體，也稱為原子）。在這一系統中，變元是帶有層次的。對於每一正整數n，都有n層的變元xn,yn等，它們表達n層對象。所以,這裡有無窮多個原始概念，即有無窮多個不同層次類型的集合。在這一形式語言中,對於任意的變元xi,yj,xi∈yj為一合法的公式,若且唯若j=i+1。沒有不附加型的對象(或變元),每一對象（或變元）都有一正整數n，使得它恰好是n型對象（或n型變元）。人們不能夠泛泛地說,所有的對象如何如何，而只能說某一型的所有對象如何如何。當某一對象並不比某一集合的型恰好小於1時,說那個對象是該集合的元素，不僅是錯誤的，而且是毫無意義（即無定義的）。人們常把這一系統記作T。T的公理是外延公理、概括公理、乘法公理和無窮公理。
① 外延公理 對於任意給定的同一型的兩個對象，例如，它們均為n型對象xn,yn,如果對於任意的n＋1型對象zn+1，使得xn在zn+1中，若且唯若yn在zn+1中,則xn與yn為同一對象，即xn=yn。形式地說，就是
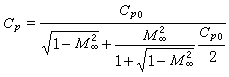
② 概括公理 對於任意的公式A(xi)，都存在一個i+1型的集合yi+1，使得
。 ③ 乘法公理 對於任意不空的i＋1型的集合xi+1，若它的任一元xi都是不空的，且xi+1的任意兩個不同的元都是不交的，則存在i型的集合yi,使得xi+1的任一元xi中恰好有一元屬於yi。反之，對於yi的任一元，xi+1也一定有一元xi,使得xi含有yi的這一相應元。形式地，就是
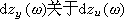
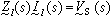，上述公式中實際上已出現了i+1型空集合與i型空集合。（下文省去了它們的下標。） ④ 無窮公理 斷定存在一個具有無窮多個元素的集合。為了嚴格地陳述這一公理，先引進一些預備概念。對於兩個同型的對象xi,yi,單元集合{xi}與無序對{xi,yi}都是i＋1型對象；有序對 <xi，yi>定義為{{xi},{xi,yi}},是i＋2型對象。這樣,以<xi,yi>為元素的集（即i型對象上的二元關係）就是i+3型的對象。為了斷定存在一無窮集合，只須斷定有無窮多個本元就夠了。關於本元的二元關係為3型集合R3。公式
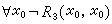表示關係 R 3 是非自反的, 這也就是說，對於任意的本元
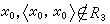。 公式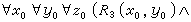 
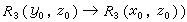表示關係R 3 是傳遞的。無窮公理的形式化陳述如下：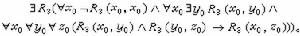 
在分支類型論中，研究的問題更為複雜。它把同一型的集合再分為不同的層次，高層次的集合不能再作為低層的集合看待。最低層次的集合稱為直謂的，決定它們的性質（謂詞）也稱為直謂的性質（謂詞），其他的集合（性質）稱為非直謂的。例如,一n+1型集合Sn+1,如果對任一n型對象xn，必須考察n+1型整體方能斷定 xn是否屬於Sn+1時,則稱集合Sn+1為非直謂的。非直謂的層次是高的。由概括公理，一性質（謂詞或公式）決定一集合，這樣，非直謂的集合可以藉助於定義它的性質來說明。例如，羅素說：一個典型的英國人具有大多數英國人所具有的性質。其中“具有大多數英國人所具有的性質”也是一種性質，可是，這一性質涉及個體性質的全體。由此，稱它是一非直謂的性質。一般說，凡涉及某一類型性質的全體而又是此類型的性質叫做非直謂的性質。從公式的角度看，例如，設z3為一3型集合,令公式A(x1)為 彐y2(x1∈y2Λy2∈z3)在其中含有1型變元x1的自由出現。由概括公理，這一公式決定一個2 型集合
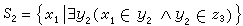。而 S2要藉助於2型集合中的約束變元來定義，也就是說,S2要藉助包括S2在內的2型集合的整體來定義。這樣，S2是一非直謂的集合，A(x1)為非直謂的公式（或稱非直謂的謂詞）。不是非直謂的集合（性質）叫做直謂的集合（性質）。 分支類型論可以避免諸如里夏爾悖論，但又遇到了新的困難。對於一個集合，人們不能籠統地說此集合的所有元素（它們是較低型的集合）都有哪些性質，而必須區分層次才能作出斷定。實數就是這樣的集合。對實數就不能作出一個單一的斷定。因此，分支類型論不能作為描述數學命題的工具。為了彌補這一缺點，羅素又增加了一條可歸約性公理或稱為還原公理：每一非直謂性質（謂詞）都有一直謂性質（謂詞）與之等價。由此，一切型的集合都是直謂的。這樣一來，又等於取消了分支類型論。
GB公理 在這GB系統中,人們把類分為集合與真類。它有集合與類兩個原始概念。用小寫英文字母 x，y，z（或加下標）作為集合變元,用大寫英文字母X,Y,Z（或加下標）作為類變元。x∈y，X∈Y，x∈X,X∈x都是初級公式。此外，clα(X)與m(X)是初級公式,它們分別表示X是一類與X是一集合。由此，使用邏輯詞獲得所有的公式。公理區分為五組：
A組公理
① сlα(x)（任意的集合x都是類）；
② X∈Y→m(X)（若類X是類Y的元素，則X是一集合。即類的任意元都是集合）；
③ (x∈X凮 x∈Y)→X=Y(類由它的元素所決定,即類的外延公理)；
④ 無序對公理（與ZF的相應公理一樣）。
B組公理（類的存在公理）
① 存在一類E，它的元素都是有序對集合，並且這一序對的第一元屬於第二元。也就是說，存在一類X,使得對於任意的集合x與y，〈x,y〉屬於X若且唯若x∈y；
② 對於任意的類X，Y，都有一類Z，它為X與Y的交類；
③ 對於任意的類X，它的補也是一類；
④ 對於任意的類X，它的元素中有序對的第一元組成一類；
⑤ 對於任意的類X,它的元作為有序對的第一元,而第二元為任意的集合，所有這些有序對組成一類；
⑥ 對於任一類X,它的逆(記為X_1)也是一類，其中X_1是這樣定義的:對於任意的集合S1,S2,有:<S1,S2>∈X若且唯若<S2,S1>∈X_1；
⑦ 對於任一類 X，存在一類Y，使得對於任意的三元組〈x,y,z〉,有〈x,y,z〉∈X若且唯若〈y,z,x〉∈Y；
⑧ 對於任一類X,存在一類Y，使得對於任意的三元組〈x,y,z〉,有〈x,y,z〉∈X若且唯若〈x,z,y〉∈Y。
C組公理（集合的存在公理）
① 無窮公理 存在一集合，它具有無窮多個元素；
② 並集合公理 任一集合的所有的元的元組成一集合；
③ 冪集合公理 任一集合的所有的子集合組成一集合；
④ 替換公理 對於描述一對一的類X,也就是說,對於任意集合y，至多有一集合z，使得〈y,z〉∈X。這時，若把X 中有序對的第一元限制在一給定的集合S1內，則X中相應於S1中元的有序對的第二元也是一集合；
不難看出，上述公理①、②、③分別與ZF中的公理⑥、④、⑤是相同的。而公理④與ZF中的公理⑧也是類似的，不同的是在那裡的前提是一具有一對一性質的公式,這裡是一對一性質的類。因此，ZF是一公理模式,而GB不是模式。不難驗證,B組公理是對應於公式的通常運算的一組公理。
D組公理（類似於ZF的正則公理） 對於任意的不空類X，都有一集合y∈X，且y與X不交。
E組公理（選擇公理） 它比ZF中的相應公理稍強一些。具體地說，存在一類 X，它的元素都是有序對集合，具有一對一的性質，亦即，對於任一集合y，恰有集合z，使得〈y,z〉∈X,且對於任一不空集合y，有z∈y，使得〈y,z〉∈X。
這五組公理中，沒有公理模式。因此，它是一有窮的公理系統。這是它的重大特點之一。它規定真類不能作為類的元素，從而擺脫了以往的悖論。
集合論公理系統並不是隨意的，而是有它的科學標準，這就是：①能夠描述康托爾理論的豐富內容，建立康托爾理論中已有的定理；②能夠擺脫以往出現的悖論；③便於解決集合論未解決的問題，中心問題是連續統假設。前兩條是基本的。當然，能否確保一系統的協調性，總是人們關心的首要問題。但是由哥德爾第二不完備性定理可知，如此豐富的集合論公理系統，如果是協調的，那么在其內部也是無法證明的，而須藉助於更強的公理才能證明。例如，若存在大基數作為一公理的話，則ZF是協調的。關於③，由哥德爾與科恩的工作可知，連續統假設在ZF（或GB）中是不可判定的，它即不能被證明，也不能被否證。換言之,在著名的集合論公理系統中,都不足以解決連續統假設。這正是人們不斷地尋求新公理系統的主要原因。人們總希望能找到科學的為大家所能接受的公理系統，並且得以解決著名的未解決的問題。
參考書目
張錦文編著：《集合論淺說》，科學出版社，北京，1984。
A.A.Fraenkel and Bar-Hillel,Foundations of Set Theory,North-Holland, Amsterdam, 1958.
K.Gdel,The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory,Princeton Univ. Press, Princeton,1940.
P.J.Cohen,Set Theory and the Continuum Hypothesis,W.A.Benjamin, New York, 1966.
R.B.Chanqui,Axiomotic Set Theory, Impredicative Theories of Classes,North-Holland, Oxford, 1981.
