概念
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。埃爾米特矩陣等於自己的共軛轉置。根據有限維的譜定理,必定存在著一個正交歸一基,可以表達自伴運算元為一個實值的對角矩陣。
基本原理
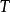 自伴運算元
自伴運算元 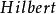 自伴運算元
自伴運算元 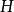 自伴運算元
自伴運算元 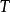 自伴運算元
自伴運算元 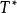 自伴運算元
自伴運算元 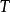 自伴運算元
自伴運算元 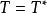 自伴運算元
自伴運算元 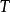 自伴運算元
自伴運算元 定義:設 是 空間 上的稠定線性運算元,如果 ⊂ ,則稱 為對稱運算元;如果 ,則稱 為自伴運算元。
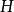 自伴運算元
自伴運算元 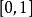 自伴運算元
自伴運算元 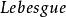 自伴運算元
自伴運算元 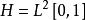 自伴運算元
自伴運算元 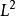 自伴運算元
自伴運算元 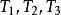 自伴運算元
自伴運算元 例子:設 為 上的 平方可積函式空間,即 ,在 上定義運算元 如下:
 自伴運算元
自伴運算元 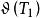 自伴運算元
自伴運算元 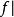 自伴運算元
自伴運算元 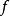 自伴運算元
自伴運算元 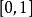 自伴運算元
自伴運算元 ={ 在 絕對連續, },
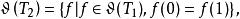 自伴運算元
自伴運算元 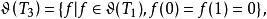 自伴運算元
自伴運算元 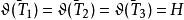 自伴運算元
自伴運算元 則 。定義運算元
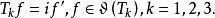 自伴運算元
自伴運算元 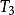 自伴運算元
自伴運算元 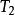 自伴運算元
自伴運算元 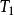 自伴運算元
自伴運算元 顯然有 ⊂ ⊂ 。下面來證明
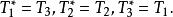 自伴運算元
自伴運算元 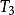 自伴運算元
自伴運算元 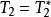 自伴運算元
自伴運算元 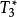 自伴運算元
自伴運算元 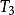 自伴運算元
自伴運算元 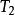 自伴運算元
自伴運算元 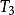 自伴運算元
自伴運算元 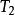 自伴運算元
自伴運算元 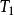 自伴運算元
自伴運算元 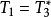 自伴運算元
自伴運算元 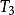 自伴運算元
自伴運算元 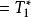 自伴運算元
自伴運算元 根據這個結果可知 ⊂ ⊂ ,故 是對稱運算元, 是對稱運算元 的自伴擴張,但作為 擴張的 滿足 ⊃ ,從而並非對稱的。
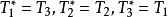 自伴運算元
自伴運算元 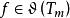 自伴運算元
自伴運算元 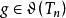 自伴運算元
自伴運算元 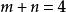 自伴運算元
自伴運算元 下面證明 。注意到 , ,其中 有
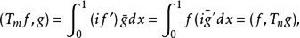 自伴運算元
自伴運算元 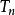 自伴運算元
自伴運算元 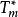 自伴運算元
自伴運算元 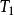 自伴運算元
自伴運算元 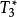 自伴運算元
自伴運算元 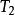 自伴運算元
自伴運算元 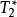 自伴運算元
自伴運算元 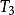 自伴運算元
自伴運算元 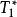 自伴運算元
自伴運算元 因此, ⊂ ,即 ⊂ , ⊂ , ⊂ 。
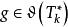 自伴運算元
自伴運算元  自伴運算元
自伴運算元 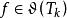 自伴運算元
自伴運算元 其次,設 , , ,對於 ,有
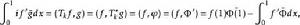 自伴運算元
自伴運算元 即
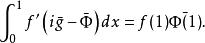 自伴運算元
自伴運算元 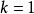 自伴運算元
自伴運算元 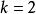 自伴運算元
自伴運算元 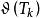 自伴運算元
自伴運算元 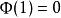 自伴運算元
自伴運算元 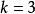 自伴運算元
自伴運算元 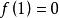 自伴運算元
自伴運算元 當 或 時,因 包含非零常數,故由上式可得 。當 時, 。這樣,總有
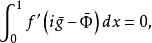 自伴運算元
自伴運算元 因而
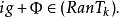 自伴運算元
自伴運算元 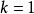 自伴運算元
自伴運算元 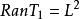 自伴運算元
自伴運算元 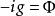 自伴運算元
自伴運算元 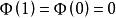 自伴運算元
自伴運算元 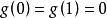 自伴運算元
自伴運算元 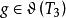 自伴運算元
自伴運算元 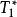 自伴運算元
自伴運算元 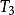 自伴運算元
自伴運算元 當 時,因 ,故 。又因 ,故 。這樣, ,即 ⊂ 。
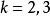 自伴運算元
自伴運算元 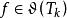 自伴運算元
自伴運算元 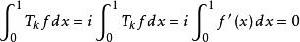 自伴運算元
自伴運算元 對 ,當 時, ,故而
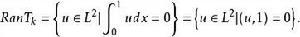 自伴運算元
自伴運算元 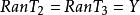 自伴運算元
自伴運算元 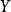 自伴運算元
自伴運算元 因而 , 是由常值函式組成的一維子空間。這樣,
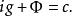 自伴運算元
自伴運算元 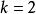 自伴運算元
自伴運算元 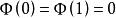 自伴運算元
自伴運算元 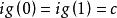 自伴運算元
自伴運算元 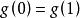 自伴運算元
自伴運算元 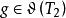 自伴運算元
自伴運算元 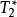 自伴運算元
自伴運算元 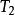 自伴運算元
自伴運算元 當 時,因 ,故 ,即 ,所以 ,即 ⊂ 。
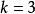 自伴運算元
自伴運算元 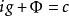 自伴運算元
自伴運算元 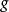 自伴運算元
自伴運算元 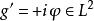 自伴運算元
自伴運算元 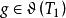 自伴運算元
自伴運算元 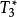 自伴運算元
自伴運算元 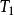 自伴運算元
自伴運算元 當 時,由 得 是絕對連續函式, ,從而 ,這樣 ⊂ 。證畢。

