定義介紹
在幾何學和拓撲學中,無窮遠直線是一個投影線,被添加到實際(仿射)平面,以便給出所產生的投影平面的入射特性的閉合和除去特殊情況。 無窮遠直線也稱為理想線。
幾何意義
在投影幾何中,任何一對線總是在某一點相交,但平行線在實際平面中不相交。將無限遠線添加到實際平面。這樣就形成了平面,因為現在的平行線在無窮遠直線上相交。此外,如果任何一對線在無窮遠直線上的某一點相交,則該對線是平行的。
每一行在某一點與無窮遠直線相交。平行線相交的點僅取決於線的斜率,而不是在y方向的截距上。
在仿射平面上,一條線在兩個相反的方向延伸。在投影平面上,一條線的兩個相反方向在無限遠的線上相交。因此,投影平面中的線是閉合曲線,即它們是循環的而不是線性的。無限本身就是這樣的;它在其兩個端點(因此實際上並不是端點)完全符合自身,因此它實際上是周期性的。
拓撲學角度
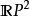 無窮遠直線
無窮遠直線無窮遠直線可以被視為圍繞仿射平面的圓。然而,圓的直徑相對的點是相同的 - 它們是相同的點。仿射平面和無窮遠直線的組合使真實的投影平面 。
雙曲線可以看作是在兩個不同點處與無限遠線相交的閉合曲線。這兩點由雙曲線的兩個漸近線的斜率指定。同樣,拋物線可以看作是一個閉合曲線,在一個點上與無限遠的線相交。這一點由拋物線軸的斜率指定。如果拋物線被其頂點切割成對稱的“喇叭”對,則這兩個喇叭變得更遠離頂點彼此平行,並且實際上平行於軸線並且彼此在無限遠處,使得它們在無限遠的線上相交。
複雜投影平面的模擬是無限遠的“線”,這是(當然)複雜的投影線。在拓撲學上,這是完全不同的,因為它是一個黎曼球體,因此它是一個2球體,被添加到C(如此四個實際尺寸)上的兩個維度的複雜仿射空間中,從而形成四維緊湊型歧管。結果是可定向的,而真正的投影平面不是。
歷史
無窮遠的複雜線在十九世紀的幾何學中被廣泛使用。事實上,最適用的技巧之一是將圓圈視為一個圓錐,限制在無窮遠處通過兩個點,下列方程的解:
X² + Y² = 0。
當我們在X和Y中刪除較低階的項時,這個方程是由任何一個圓的形式。更正式地,我們應該使用均勻坐標:
[X:Y:Z]
並注意無限遠的行通過設定來指定:
Z = 0。
通過引入Z的能量,然後設定Z = 0來使等式均勻化,精確地消除低階條件。
因此,解決這個方程,我們發現所有的圓圈都能通過無限遠的循環點:
I = [1:i:0]和J = [1:-i:0]。
這些當然是複雜的點,任何代表一組齊次坐標。由於投影具有足夠大的對稱性,所以它們並不是特別的。結論是,三參數族圓可以被視為通過兩個給定的不同點P和Q的圓錐曲線的線性系統的特殊情況。
