數的幾何
正文
又稱幾何數論，套用幾何方法研究某些數論問題的一個數論分支。它的一類典型問題為：設 ƒ(x1,x2,…,xn)是實變數x1,x2, …, xn的實值函式，對於適當選取的整數u1,u2,…un，｜ƒ(u1,u2,…un)｜的值能有多小？例如,設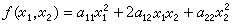
是一個正定二次型，用數的幾何方法可以證明，存在不全為零的整數u1,u2，使得 
，
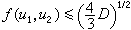是型的判別式。 17～18世紀間,J.-L.拉格朗日和C.F.高斯等就已開始以幾何觀點研究二次型的算術性質。1891年，H.閔科夫斯基發表了數的幾何第一篇論文，並於1896年出版了《數的幾何學》一書。從此，數的幾何成為數論的一個獨立分支。
數的幾何是研究丟番圖逼近、代數數論的重要工具。
用Rn表示n維實歐幾里得空間，如果
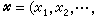
的所有坐標都是整數，那么尣稱為一個(n維)整點或格點。全體n維整點的集合記作Λ0。設點集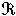
嶅Rn，λ是一個實數，把所有形如
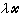(尣∈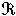)的點組成的集記為
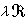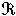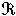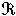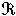。如果=-，亦即若尣∈，則-尣∈，那么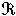稱為關於原點對稱，或簡稱為對稱。如果當含有尣、у時必含有連線尣、у的線段,亦即含有一切形如(1-θ)尣+θу(0≤θ≤1)的點，則稱為凸集。關於原點對稱的凸集，稱為對稱凸集。 一個重要的對稱凸集，是由以下的一組實線性型定義的：
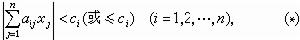
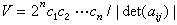。如果(*)中全是“≤”，那么它就定義了一個閉集。 閔科夫斯基研究了對稱凸集的基本性質，獲得數的幾何第一基本定理：如果
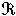嶅Rn是體積為V(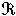)（可能為無窮）的對稱凸集，且V(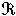)≥2n, 那么在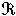中或其邊界上必有一個非零整點。 這個定理套用於集(A),得到著名的閔科夫斯基線性型定理：如果正實數с1，с2，…，сn適合с1с2 … сn≥｜det(αij)｜,那么存在不同時為零的整數x1,x2,…,xn,滿足不等式組
。
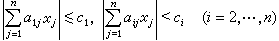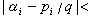
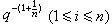。此外，上述定理還可用於解決代數數域的基數問題。 有時，需要考慮
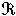中含有多少個線性無關的整點。設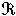是閉的對稱凸集,0<V(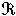)<∞。對於尣∈Rn,定義距離函式
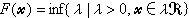，若右式不存在，則令F(尣)=∞。於是0≤F(尣)≤∞,F(λ尣)=λF(尣)(當λ>0),並且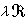={尣｜F(尣)≤λ}(λ≥0)。對於集(A)（其中全取“≤”），
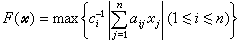。 由F(尣)的性質可知，對每個i(1≤i≤n，存在最小的λ=λj，使
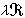含有i個線性無關的整點。λj稱為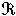的第i個相繼極小，亦即 
，
， 
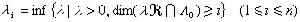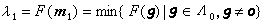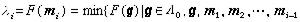線性無關｝(i≥2)。 例如,對於超立方體｜xj｜≤1(1≤i≤n),λj=1(i=1,2,…,n),mj可取作單位矢(0,…，0，1，0，…，0)。
顯然，
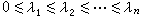，由閔科夫斯基關於數的幾何第一基本定理可知，
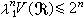。 閔科夫斯基進而得到數的幾何第二基本定理：設
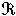是閉的對稱凸集，0<V(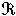)<∞,則其相繼極小λ1,λ2,…,λn適合不等式 
。
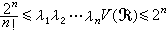參考書目
J.W.S.Cassels,An Introduction to the Geometry of Number,Springer-Verlag,Berlin,1959.
