同調論
正文
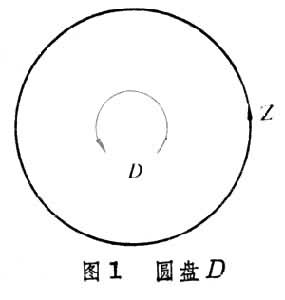
代數拓撲學中的一個主要組成部分,研究與同調概念有關的課題。考慮帶有方向的曲面(塊)與曲線(段),如圖1、圖2中的圓盤均由鏇轉箭頭定向。圓周Z與Z┡是比D與D┡低一維的圖形,作為曲線,它們各按所標的箭頭定向。規定D的邊緣為Z,記作嬠D=Z;對於D┡,則應有嬠D┡=-Z┡。無底圓筒 C與它的上下邊界W1與W0按所標箭頭定向後有嬠C=W1-W0(圖3)。在圖 4環面T中,圓圈Z為曲面塊 A的邊緣,嬠A=Z,這時稱閉曲線Z在環面T上同調於零,記作Z~0。閉曲線W在T上不同調於零,但嬠B=W-W1,這時稱閉曲線W同調於W1,記作W~W1。同調概念就是在這種定向圖形之間的邊緣關係上建立起來的。
 同調論
同調論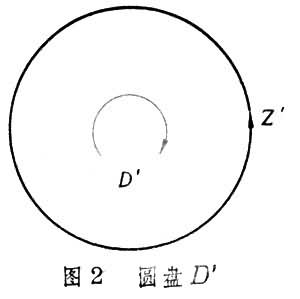 同調論
同調論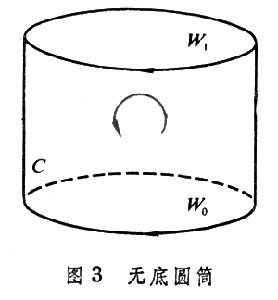 同調論
同調論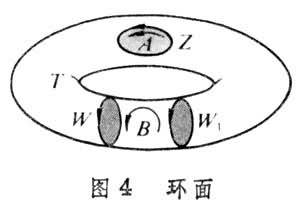 同調論
同調論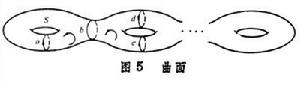 的曲面S上,α、с、d都不同調於零,b)~0,α不同調於с、d中的任何一個,但с~d。
的曲面S上,α、с、d都不同調於零,b)~0,α不同調於с、d中的任何一個,但с~d。 將圖6
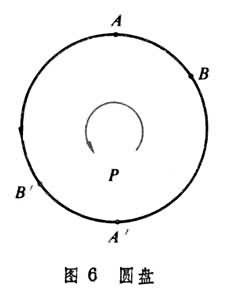 中圓盤邊界上的每一對對徑點(諸如A與A┡,B與B┡)粘合,得到的曲面p叫做射影平面。
中圓盤邊界上的每一對對徑點(諸如A與A┡,B與B┡)粘合,得到的曲面p叫做射影平面。 與
與 在p中為同一定向圓圈z。可以看出,在p中有z+z=2z~0,但z不同調於零。
在p中為同一定向圓圈z。可以看出,在p中有z+z=2z~0,但z不同調於零。 H.龐加萊從1895年起,為了對同調概念做一般的討論,引進了可剖分為復形的空間,從此產生了組合拓撲學。
n維單形 0維單形是一個點,一維單形是一條線段,二維單形是一個三角形,三維單形是一個四面體,n維單形是一個具有n+1個頂點的廣義四面體。
定向單形 除0維單形不給定向外,其他維的單形可以有兩個定向。例如,一維單形的定向可以用從起點到終點的箭頭給出,二維單形的定向可以用一個鏇轉方向給出(圖7
 ),等等。一般對於n維單形有兩個定向,可以用頂點的順序來給出它的定向。彼此相差一個偶排列的兩個順序代表同一個定向。例如,線段AB的一個定向可以用(A,B)表示,另一個定向則可用(B,A)表示;三角形ABC的一個定向可用(B,A,C)或(C,B,A)或(A,C,B)表示,另一個定向可用(B,C,A,)或(C,A,B)或(A,B,C)表示。
),等等。一般對於n維單形有兩個定向,可以用頂點的順序來給出它的定向。彼此相差一個偶排列的兩個順序代表同一個定向。例如,線段AB的一個定向可以用(A,B)表示,另一個定向則可用(B,A)表示;三角形ABC的一個定向可用(B,A,C)或(C,B,A)或(A,C,B)表示,另一個定向可用(B,C,A,)或(C,A,B)或(A,B,C)表示。 單純復形 是由有限個單形很好地拼湊起來而組成的。例如,圖8
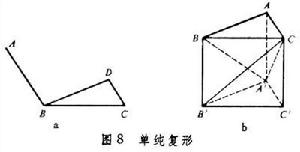 之a這個單純復形是由4個0維單形A,B,C,D;4個一維單形AB,BD,CD,BC和1個二維單形BCD按照圖8之a中所畫的關係拼湊而組成的。圖8之b這個單純復形是由6個0維單形A,B,C,A┡,B┡,C┡,12個一維單形AB,BC,CA,A┡B┡,B┡C┡,C┡A┡,B┡C,A┡C,A┡B,BB┡,AA┡,CC┡,6個二維單形AA┡B,A┡BB┡,BB┡C,B┡CC┡,CC┡A┡,CA┡A按照圖8之b中所畫的關係拼湊而組成的。
之a這個單純復形是由4個0維單形A,B,C,D;4個一維單形AB,BD,CD,BC和1個二維單形BCD按照圖8之a中所畫的關係拼湊而組成的。圖8之b這個單純復形是由6個0維單形A,B,C,A┡,B┡,C┡,12個一維單形AB,BC,CA,A┡B┡,B┡C┡,C┡A┡,B┡C,A┡C,A┡B,BB┡,AA┡,CC┡,6個二維單形AA┡B,A┡BB┡,BB┡C,B┡CC┡,CC┡A┡,CA┡A按照圖8之b中所畫的關係拼湊而組成的。 單純復形的n維鏈 形如
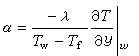 的線性組合叫一個n維鏈,其中{
的線性組合叫一個n維鏈,其中{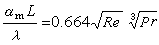 }取遍單純復形K的所有單形,且每個單形取好了定向(0維單形不取定向),αi為整數(即線性組合中的每一項是K中的一個n維定向單形,且附一個整係數)。兩個n維鏈之和定義為一個n維鏈,其每項的係數是兩個鏈的相應項的係數之和。容易驗證:K的所有的n維鏈組成一個交換群,這個交換群叫K的n維鏈群,記作Cn(K)。例如,圖8之a 中的單純復形,3(A,B)+2(B,C)-(C,D)-5(B,D)為一個一維鏈;圖8之b中的單純復形,4(A,A┡,B)-2(B,B┡,C)+(C,A,A┡)為一個二維鏈。
}取遍單純復形K的所有單形,且每個單形取好了定向(0維單形不取定向),αi為整數(即線性組合中的每一項是K中的一個n維定向單形,且附一個整係數)。兩個n維鏈之和定義為一個n維鏈,其每項的係數是兩個鏈的相應項的係數之和。容易驗證:K的所有的n維鏈組成一個交換群,這個交換群叫K的n維鏈群,記作Cn(K)。例如,圖8之a 中的單純復形,3(A,B)+2(B,C)-(C,D)-5(B,D)為一個一維鏈;圖8之b中的單純復形,4(A,A┡,B)-2(B,B┡,C)+(C,A,A┡)為一個二維鏈。 邊緣運算元 規定0維單形的邊緣為零,一維定向單形(A,B)的邊緣為B-A,二維定向單形(A,B,C)的邊緣為(B,C)-(A,C)+(A,B),三維定向單形(A,B,C,D)的邊緣為(B,C,D)-(A,C,D)+(A,B,D)-(A,B,C),等等。可類似地定義n維定向單形的邊緣。以符號嬠寫在定向單形的前面表示它的邊緣。對於每一個n維鏈
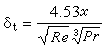 ,規定它的邊緣
,規定它的邊緣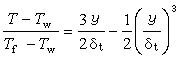 (即先取它的每一個定向單形的邊緣再乘上它的原來係數然後求和)。不難看出,一個n維鏈的邊緣是一個n-1維鏈。由此得到從n維鏈群到n-1維鏈群的同態,這個同態叫做(下)邊緣運算元,記作嬠:Cn(K)→Cn-1(K)。邊緣運算元具有嬠嬠=0的性質。
(即先取它的每一個定向單形的邊緣再乘上它的原來係數然後求和)。不難看出,一個n維鏈的邊緣是一個n-1維鏈。由此得到從n維鏈群到n-1維鏈群的同態,這個同態叫做(下)邊緣運算元,記作嬠:Cn(K)→Cn-1(K)。邊緣運算元具有嬠嬠=0的性質。 n維閉鏈 滿足嬠x=0的n維鏈x叫n維閉鏈。例如,圖8a中的單純復形,一維鏈(C,D)-(B,D)+(B,C)就是一個一維閉鏈。單純復形K的所有n維閉鏈所組成的交換群叫K的n維閉鏈群,記作Zn(K)。
n維邊緣鏈 如果一個n維鏈是某一個 n+1維鏈的邊緣,則稱此鏈為n維邊緣鏈(即一個n維圖形是n+1維圖形的邊緣)。例如圖8a中的單純復形,一維鏈(C,D)-(B,D)+(B,C)=嬠(B,C,D)就是一個一維邊緣鏈。單純復形K的所有n維邊緣鏈所組成的交換群叫K的n維邊緣鏈群,記作Bn(K)。由於邊緣鏈一定是閉鏈,因而Bn(K)是Zn(K)的子群。
n維同調群 由於Bn(K)是 Zn(K)的子群,把商群Zn(K)/Bn(K)叫做單純復形K的n維(下)同調群,記作Hn(K)。Hn(K)中的每一個元素叫做一個n維同調類。如果兩個n維閉鏈zń,z怽的差為一個邊緣鏈時,就叫zń與z怽同調。如果zn是邊緣鏈,則稱zn同調於零。例如,圖8b中的單純復形,2個一維閉鏈(A,B)+(C,A)+(B,C),(A┡,B┡)+(C┡,A┡)+(B┡,C┡)有嬠((A,B,A┡)+(A┡,B,B┡)+(B,C,B┡)-(C,B┡,C┡)-(C,C┡,A┡)-(C,A┡,A))=((A,B)+(C,A)+(B,C))-((A┡,B┡)+(C┡,A┡)+(B┡,C┡))。因而這兩個閉鏈同調(而它們都不同調於零)。同調群 Hn(K)的秩叫做K的n維貝蒂數。如果在n維鏈群的定義中,用任意的一個交換群G中的元素代替整數,可以得到以G為係數的n維鏈群 Cn(K;G)。相似地有以G為係數的n維邊緣群Bn(K;G),n維閉鏈群Zn(K;G)。由此定義以G為係數的n維同調群Hn(K;G)。
多面體 單純復形 K的全體單形的並集叫做一個多面體,記作│K│。對於多面體的同調群Hn(|K|;G)可以用Hn(K;G)來定義,即令Hn(|K|;G)=Hn(K;G)。
單純映射 給定了兩個單純復形K,L,且指定了K的每一個頂點(0維單形)到L的某個頂點的一個對應,並把K中的屬於同一個單形的所有頂點對應到L的同在一個單形中的頂點,這個對應叫從K到L的單純映射。單純映射ƒ:K→L把 K中的每一個定向單形(頂點的一個順序)映射到L中的一個定向單形(得到對應頂點的一個順序,若有兩個頂點的像重合,則理解為對應到0),由此產生了一個從Cn(K;G)到 Cn(L;G)的同態,並且可以證明它把Zn(K;G)映射到Zn(L;G),Bn(K;G)映射到Bn(L;G)。從這個同態可以導出一個從Hn(K;G)到Hn(L;G)的同態。
連續映射導出的同態 給了兩個多面體|K|、|L|之間的一個連續映射F:│K│→│L│,可以將K適當重分成另一復形K┡,並用一個單純映射去逼近F。利用這個單純映射導出的同調群之間的同態得到Hn(│K┡│;G)到Hn(│L│;G)的同態,並且可以證明,Hn(│K┡│;G)與Hn(|K|;G)自然地同構。 於是記此同態為Fn:Hn(|K|;G)→Hn(│L│;G)。
上同調群 G為任一交換群,Hom(Cn(K),G)為所有從Cn(K)到G的群同態所組成的群,這個群叫做K的以G為係數的 n維上鏈群,記作Cn(K;G)。利用K 的邊緣運算元嬠:Cn(K)→Cn-1(K)可得對偶同態δ:Cn-1(K;G)→Cn(K;G)。定義如下:設ƒ∈Cn-1(K;G),規定δƒ=ƒ嬠:Cn(K)→G。這個δ叫上邊緣運算元,具有δδ=0的性質。與同調群的定義相似,可以定義以G為係數的上閉鏈群Zn(K;G),上邊緣鏈群Bn(K;G),上同調群Hn(K;G)。當G為整數加群Z時,省去符號Z,簡單記為 Cn(K),Zn(K),Bn(K),Hn(K),等等。對於連續映射F:│K│→│L│,利用單純映射去逼近,可得到同態
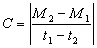
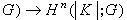 。上同調群的構造可以由同調群完全確定。當多面體│K│為定向流形時,同調群和上同調群之間還有對偶關係(流形的龐加萊對偶定理),即Hn(|K|;G)同構於Hq-n(│K│;G),其中q為流形│K│的維數。
。上同調群的構造可以由同調群完全確定。當多面體│K│為定向流形時,同調群和上同調群之間還有對偶關係(流形的龐加萊對偶定理),即Hn(|K|;G)同構於Hq-n(│K│;G),其中q為流形│K│的維數。 J.W.亞歷山大在1915年證明了多面體的同調群的拓撲不變性,即如果兩個多面體│K│,│L│同胚,那么這個同胚誘導它們的上同調群、同調群的同構。實際上,如果│K│,│L│倫型相同,其同倫等價也誘導它們的上同調群、同調群的同構。
利用同調群可以解決不少幾何問題。例如,布勞威爾不動點定理(見不動點理論),可以找到歐拉示性數與貝蒂數之間的關係式:
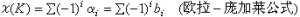
 (K)即K的歐拉示性數。從而證明了歐拉示性數是│K│的拓撲不變數。
(K)即K的歐拉示性數。從而證明了歐拉示性數是│K│的拓撲不變數。 單純復形的整係數同調群是個有限生成的交換群。因此,它同構於
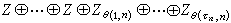 ,其中Z代表整數加群,θ(1,n),…,θ(τn,n)為一串自然數,每個可整除後一個,嘰表示直和。前面Z的個數即為n維貝蒂數;後面這串有限群的階數θ(1,n),…,θ(τn,n)稱為 n維撓係數。確定一個單純復形(及其多面體)的各維貝蒂數與撓係數,也就算出了同調群。
,其中Z代表整數加群,θ(1,n),…,θ(τn,n)為一串自然數,每個可整除後一個,嘰表示直和。前面Z的個數即為n維貝蒂數;後面這串有限群的階數θ(1,n),…,θ(τn,n)稱為 n維撓係數。確定一個單純復形(及其多面體)的各維貝蒂數與撓係數,也就算出了同調群。 簡單的單純復形的同調群的計算,可以通過叫做"擠到邊上去"的方法直觀地解決。一般單純復形同調群的計算,可以用矩陣變換的方法經有限多次的算術運算解決,不過具體實現這種計算是非常困難的。
帶係數群G的同調群的構造,可由整係數同調群與G按照“泛係數”公式來求。上同調群的計算也有其相應的公式。
同調論的公理 S.艾倫伯格和N.E.斯廷羅德提出了同調群、上同調群滿足的公理,並證明了在多面體的情形下滿足公理的同調群、上同調群是惟一的。
在一般的拓撲空間上引進同調群主要有兩種方式。利用有序單形映射到拓撲空間,來定義這個拓撲空間的同調群,稱為這個拓撲空間的奇異同調群;利用單純復形來逼近一個拓撲空間,用極限來定義這個拓撲空間的同調群,稱為這個拓撲空間的切赫同調群。在緊多面體的情況,這兩種同調群都同構於按單純剖分得到的同調群。
在以某種環為係數的上同調群中可以引入乘法使之成為上同調環。為了更好地利用上同調群,在其上引入了所謂上同調運算的額外結構,例如斯廷羅德冪,龐特里亞金冪等等。由斯廷羅德冪發展成為斯廷羅德代數的研究,大大豐富了同調論的內容。
參考書目
江澤涵著:《拓撲學引論》,上海科學技術出版社,上海,1978。
R.M. Switzer,Algebraic Topology-Homotopy and homology, Springer-Verlag, New York, 1975.
