同調代數

同調代數，是代數學的一個非常重要的分支，是由美國的數學家與歐洲的數學家在20世紀40年代彼此獨立而幾乎同時開始發展起來的。

同調代數

正文

代數學的一個非常重要的分支，是由美國的數學家與歐洲的數學家在20世紀40年代彼此獨立而幾乎同時開始發展起來的。同調代數源出於代數拓撲學，因而它仍保留著一些代數拓撲學中所用的術語，如循環（閒鏈）、邊緣（邊緣鏈）等等，而代數拓撲學本來就是把幾何概念轉換成代數概念的一種理論。
代數拓撲學中的同調群概念與同調代數有密切聯繫。在n維歐氏空間En中適當取q+1個點α0,α1,…,αq，q≤n，它們將張成一個q維超平面。取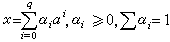，則所有這些x之集成為一個q維單形Sq,常記為(α0,α1,…,αq)。它以αi為其頂點,αi全為正數的點稱為內點,其餘的點,稱為邊緣點。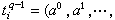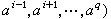稱為其一個邊緣面,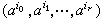是一個r維面，這裡i0,i1,…,ir是0,1,…,q中的任何r+1個數,取C為En中有限個單形之集,其中任兩個單形之交或為空集,或為它們的一個r維面，而且若Sq屬於C,則其任一個r維面也必屬於C。以Cq表示由C中所用的q維單形Sq所生成的加法自由交換群，並於Sq=(α0,α1,…,αq)時，定義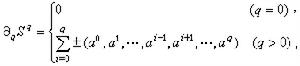

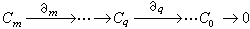這裡的±號是按照某種定向規則而確定的，於是得到一個鏈復形

,　(1)

且嬠q-1嬠q=0，所以Im嬠q吇Ker嬠q-1（Im嬠是嬠的像,Ker嬠是嬠的核）,這時,商群Hq=Ker嬠q/Im嬠q+1稱為C的第q個同調群，同調群的理論集中地反映出復形的有關其邊緣的幾何性質。“同調”一詞源出希臘文,意指“和諧”或“一致”。
代數學家不考慮上述同調理論中的幾何意義，直接討論式(1)，研究其同調群,式中的Ci已不僅是一些交換群,而是環上的模。同調代數的理論已經變成研究環、一般代數、李代數與群的一種不可缺少的有力工具。　
以下述及的環U與B都有單位元，模都是酉模，且一般是左U模。左U模範疇記作。
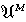復形與同調模　範疇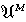中的一個復形是一列(A,嬠)

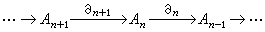,　(2)

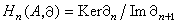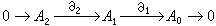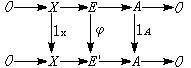
式中An都是U模,嬠n是模同態,而且嬠n-1嬠n=0, Ker嬠n稱為n循環,lm嬠n+1稱為n邊緣。於是Im嬠n+1吇Ker嬠n，定義是復形(A，嬠)的第n個同調模。若式(2)中對所有的n都有Im嬠n+1=Ker嬠n,即所有Hn(A,嬠)都等於0，則(A,嬠)是一個正合列。特別,若在n≥3與n<0時，所有的 An都等於 0，而(2)又正合，則為短正合列,這時嬠2必為單同態,嬠1必為滿同態，而A0=A1/嬠2A2。
假定(B,d)也是一個復形, 設有模同態ƒn:An→Bn,使下圖可交換

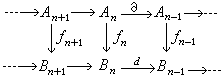
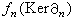
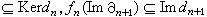則ƒ={ƒn}稱為由(A,嬠)到(B,d)的一個復形映射。於是,以所有的U模的復形為對象,以復形映射為態射,則得一個阿貝爾範疇,稱為復形範疇,記為Ucm。由於,所以,ƒn將引出Hn(A,嬠)到Hn(B,d)的一個模同態ƒn,稱為同調映射。若ƒ與g都是(A,嬠)到(B,d)的復形映射，且有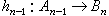，使對所有的n，恆有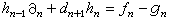,則ƒ與g為同倫的，記為h:ƒ埍g，這時必有ƒn=gn。
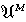固定任一整數n,每一個復形(A,嬠)將對應其第n個同調模Hn(A,嬠),而復形映射ƒ:(A,嬠→(B,d)將引出同調映射ƒn, 因此Hn是一個由Ucm到的函子,它把(A, 嬠)變成Hn(A,嬠),把ƒ:(A,嬠)→(B,d)變成ƒn，這個Hn稱為第n個同調函子。
復形的短正合列 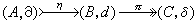是指如下的交換圖：

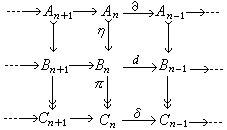　(3)

其中各行均為復形, 各列均為短正合列, 表單同態，表滿同態。對於(3), 有在同調代數中各個方面都起著重要作用的同調正合列定理：
有連線映射(模同態) 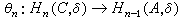使有正合列（δ，嬠，d 等記號都省掉）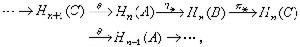

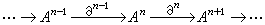與上述同調相對偶的是上同調。設An為U模，則

　(4)

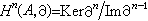稱為上復形,式中嬠n嬠n-1=0,而商模稱為上復形(4)的第n個上同調模。
投射分解與內射分解　正合列

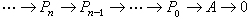,　(5)

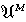當p0,p1,p2,…,pn,…都是投射模時,稱為A的投射分解。由於每一個U模都是一個投射模的同態像，所以，每一個U模A都有投射分解。如果(5)中存在一個最小的n,使Im嬠n為投射模,那么,儘管A的投射分解並不惟一(可能有其他的投射分解)，這個n卻是不變的,稱為A的投射維數, 記為PdA=n。如果每一個lm嬠n都不投射,那么PdA=∞。於是,PdA=0的意思就是A為投射模；若PdA=1,則A可分解成兩個投射模之商，A=p0/p1；若PdA=2,則A是三個投射模之商，A=p0/p1/p2,…。 範疇中各模的最大投射維數是這個範疇的一個總體性質，因而也是環U本身的一個總體性質，所以稱為U的左總體維數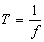。已知:若ldU=0,則U為滿足極小條件的半單環;若ldU=1,則U為左遺傳環。同樣可定義U的右總體維數rdU。一般說來，U的左、右總體維數並不相等。
與上述投射分解相對偶，正合列

，

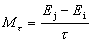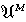當I0,I1,…都是內射模時，稱為A的內射分解。由於每一個A都可嵌入到一個內射模內，所以A的內射分解一定存在。同樣可定義A 的內射維數IdA。在中各模的最大內射維數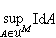正好等於U的左總體維數ldU。
導函子　設T是一個自 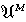到BM 的共變加法函子,由下列的辦法來定義的一系列新的函子LnT與RnT，稱為由T 所導出的導函子。
取A與B均為U模，ƒ:A→B為模同態,(p,嬠)與(Q,d)分別為A與B的投射分解，則有復形映射{ƒn}使有交換圖

於是有交換圖

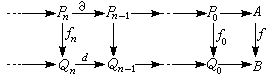
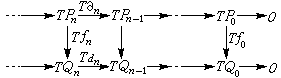(6)

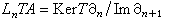這裡兩行都是B模的復形，它們的第 n個同調模，將表以與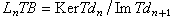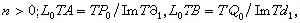， 而由Tƒn所引出的同調映射則表以LnT(ƒ),其實這些LnTA與LnTB並不隨所取的投射分解而變，換成A與B的其他的投射分解，仍得到同樣的LnTA與LnTB。同時,LnT(ƒ)也不隨所取的復形映射{ƒn}而變,換ƒn為gn,只要圖(6)仍然是可交換的，那么就有相同的同調映射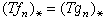。 因此,由A變成LnTA，由ƒ:A→B得到LnT(ƒ)，則得一個共變函子LnT，稱為T的左導函子。
若改用A的內射分解，則用同樣的方法可得到T的右導出函子RnT，它是一個共變函子。
如果 F是一個逆變加法函子，那么取 A的投射分解(p,嬠)，就得上復形(Fp，F嬠),其第n個上同調模將記為RnF(A)，因而可由F導出的右導出函子RnF,它是一個逆變函子。
若對所有的n>0恆有LnTA＝0，則A稱為一個左T-零調模。零調模在譜序列的理論中非常重要。
函子圱與Tor　取M為右U模,對任一個左U模,定義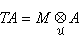,並對模同態σ:A→B,令T(σ)=1圱σ:M圱A→M圱B, 則得一個由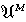到交換群範疇AG的共變加法函子T,此T也常表成M圱-。由T所導出的第n個左導出函子將表以Tor將(M,-)，換言之,若取A的一個投射分解為(p,嬠),則得一個復形(M圱p,1圱嬠)，此復形的第n個同調模就是Torn(M,A)(U有時可省去)。特別，Tor0(M,A)=M圱A。
同樣，讓A固定，則得函子－圱A，由其導出的第n個導出函子為Torn(-,A)，所以Torn(-,-)實際上是一種雙函子，它對兩個變數（讓其一固定，另一個變動）都是共變加法函子。
符號Tor是英文TORSION一字的前三個字母，它的意思是“撓性質”。假定U是一個整環（無零因子的交換環）,而A是一個U模，讓tA={α∈A│有某一非零α∈U，使αα=0},於是tA是A的一個子模,稱為A的撓子模。讓A對應tA即得 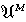到其自身的一個共變函子t；另一方面,讓Q為U的商域（也看成U模）,令M=Q/U為商模，則可證明，函子t（可稱為撓函子）與函子Tor(M,－)是自然等價的，故用符號Tor。
函子Hom與Ext　固定一個左U模x，對於任一個左U模A，定義 FA=HomU(A,x)，並對ƒ:A→B，定義F(ƒ)：Hom(B,x)→Hom(A,x),使在σ∈Hom(B,x)時有交換圖(7)。

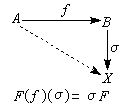(7)

F(ƒ)(σ)=σF,於是,F是一個由 到AG的逆變函子，其第n個右導出函子RnF將表以Ext(-,x)。因此,先取A的任一個投射分解(ρ,嬠)，再作上復形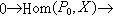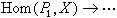, 則其第n個上同調模就是 Extn(A,x)，特別，Ext0(A,x)=Hom(A,x)。
如果讓A固定，令TX=Hom(A，x)，並對g:x→Y,定義T(g):Hom(A,x)→Hom(A,Y),使T(g)(τ)=gτ如交換圖(8)，則T為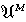到AG的共變函子, 其第n個右導出函子將表以Extn(A,-)，換言之，Extn(-,-)是一個雙函子，它對第一個變數A是逆變的（讓x 固定時）；而對第二個變數x是共變的（讓A固定）。

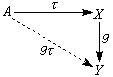(8)

與Tor的情況類似，Ext是英文 Extension一字的前三個字母組成的符號，其意為“擴張”。設x與A都是U模，E稱為x由A的一個模擴張，是指有短正合列0→x→E→A→0。兩個擴張E與E┡稱為等價的,意指有φ:E→E┡使下圖可交換

這裡的φ必是一個模同構,因而上述等價性是一種等價關係，以e(x,A)表所有等價類之集合，可以證明，e(x,A)與Ext1(A，x)是一一對應的。所以可認定e(x，A)就是Ext1(A,x)。
群的同調與上同調　設G為乘法群，Z表整數環，以G的所有的元素為生成元素可得一個加法自由群ZG,因此ZG 中每一個元素都惟一地表成 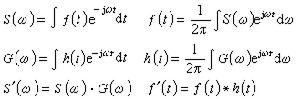的形狀，這裡m(x)∈Z，且只能有有限個m(x)不為0,再定義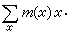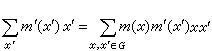，則 ZG是一個環,稱為Z上的群環。任一個ZG模也稱為G模。如果在z∈Z時,定義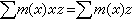，則Z作成一個左G模。
當A為G模時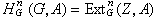， 稱為G的其係數在A內的上同調群。對偶地,若B為右G模,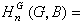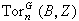稱為G 的其係數都在B內的同調群。不難證明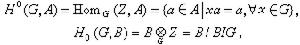

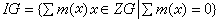這裡的稱為ZG的增廣理想，它在群的同調理論中十分重要。
各種群的 Hn與Hn的計算與理論是同調代數與群論中的重要研究課題。
譜序列　它是同調代數中的一個重要的理論，也是一種研究同調模的重要方法。
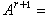
設A是一個U模,若有模自同態d:A→A使B=Imd吇Z=Ker d,即dd=0,則(A,d)稱為一個微分模,d是其微分,而商模Z/B是(A，d)的同調模H(A,d)。與復形的情況類似，B為d的邊緣,而Z為d的循環。微分模的序列{Ar,dr}(r≥1 是整數)稱為一個譜序列，是指對每一個r都有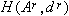。讓Z2Ker d1,B2=Im d1,則A2=Z2/B2,又定義Z3與B3,使A3=Kerd2/Imd2=(Z3/B2)/(B3/B2)=Z3/B3,…,依此類推,可讓Ar=Zr/Br,於是得一鏈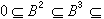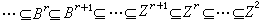，令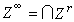,,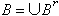則A∞=Z∞/B∞稱為譜序列{Ar,dr}的極限模。在r很大時，Ar可作為極限模的“近似”。
在同調代數中常用到的譜序列實際上是由雙分次模所組成的，所謂雙分次模，就是一些模Epq的集合，p與q都是整數。設E與D都是雙分次模,且有整數對(α,b)),使對任何p、q都有一個模同態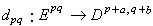，則d:E→D稱為具有雙分次(α,b))的映射。若d:E→E有次數(α,b)),且dd=0，即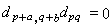,凬p,q，則d是微分，而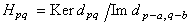為其同調雙分次模。假定(Er,dr)都是微分雙分次模,且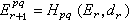,那么，這對於(Er,dr)也是一個譜序列。
用過濾的辦法,可以從一個復形(A,嬠)得到一個很有用處的譜序列。假定對每一個p∈Z，FpA都是A的一個子復形，並且有

,

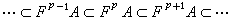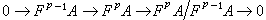則F稱為復形(A,嬠)的一個過濾。於是,對任何p就有一個復形的短正合列，由同調正合列定理，得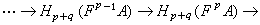

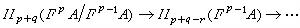, (9)

讓

,

式(9)就可改寫為

,

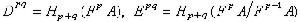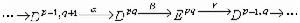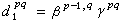這裡α，β，γ是有次數(1，-1)，(0,0)與(-1，0)的映射。以E1表示雙分次模{Epq},並取，易知，d1:E→E有次數(-1,0),且d1d1=0,故d1是E1的微分。以E2表其同調雙分次模，再適當定義d2:E2→E2為E2的微分。依此類推,即得一個譜序列(Er,dr),只要F取得恰當，這個譜序列可以提供(A,嬠)的同調模的一些信息。
參考書目
　H.Cartan and S.Eilenberg,Homological Algebra, Princeton Univ. Press, Princeton, 1956.
　S.MacLane,homology, Springer-Verlag, Berlin, 1963.
　J.J.Rotmann,An Introduction to Homological Algebra,Academic Press, New York, 1979.

配圖

相關連線