簡介
基本簡介
“裝錯信封問題”是由當時最有名的數學家約翰·伯努利(Johann Bernoulli,1667-1748)的兒子丹尼爾·伯努利(DanidBernoulli,1700-1782)提出來的,大意如下:
一個人寫了n封不同的信及相應的n個不同的信封,他把這n封信都裝錯了信封,問都裝錯信封的裝法有多少種?
公式證明
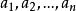 全錯位排列
全錯位排列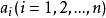 全錯位排列
全錯位排列n個相異的元素排成一排 。則 不在第i位的排列數為:
證明:
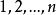 全錯位排列
全錯位排列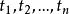 全錯位排列
全錯位排列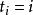 全錯位排列
全錯位排列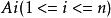 全錯位排列
全錯位排列設 的全排列 的集合為I,而使 的全排列的集合記為 ,
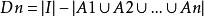 全錯位排列
全錯位排列則 .
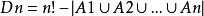 全錯位排列
全錯位排列所以 .
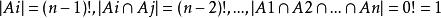 全錯位排列
全錯位排列注意到 。
由容斥原理:
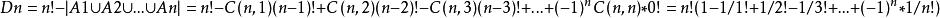 全錯位排列
全錯位排列研究錯排問題的方法
枚舉法
對於情況較少的排列,可以使用枚舉法。
•當n=1時,全排列只有一種,不是錯排,D= 0。
•當n=2時,全排列有兩種,即1、2和2、1,後者是錯排,D= 1。
•當n=3時,全排列有六種,即1、2、3;1、3、2;2、1、3;2、3、1;3、1、2;3、2、1,其中只有有3、1、2和2、3、1是錯排,D=2。用同樣的方法可以知道D=9。
•最小的幾個錯排數是:D= 0,D= 1,D=2,D= 9,D= 44,D= 265,D= 1854.
遞推數列法
對於排列數較多的情況,難以採用枚舉法。這時可以用遞歸思想推導錯排數的遞迴關係式。
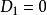 全錯位排列
全錯位排列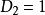 全錯位排列
全錯位排列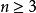 全錯位排列
全錯位排列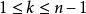 全錯位排列
全錯位排列顯然 , 。當 時,不妨設n排在了第k位,其中k≠n,也就是 。那么考慮第n位的情況。
•當k排在第n位時,除了n和k以外還有n-2個數,其錯排數為D。
•當k不排在第n位時,那么將第n位重新考慮成一個新的“第k位”,這時的包括k在內的剩下n-1個數的每一種錯排,都等價於只有n-1個數時的錯排(只是其中的第k位會換成第n位)。其錯排數為D。
所以當n排在第k位時共有D+D種錯排方法,又k有從1到n-1共n-1種取法,我們可以得到:
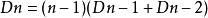 全錯位排列
全錯位排列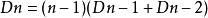 全錯位排列
全錯位排列在上面我們得到 從這個公式中我們可以推出D的通項公式,方法如下:
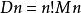 全錯位排列
全錯位排列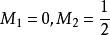 全錯位排列
全錯位排列為書寫方便,記 ,則
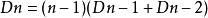 全錯位排列
全錯位排列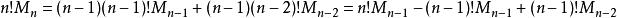 全錯位排列
全錯位排列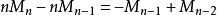 全錯位排列
全錯位排列當n大於等於3時,由 ,即 。 所以, 。
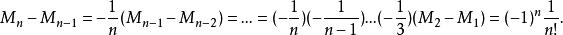 全錯位排列
全錯位排列於是有
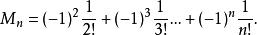 全錯位排列
全錯位排列將上面式子分邊累加,得
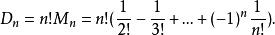 全錯位排列
全錯位排列因此,我們得到錯排公式
多項式模擬
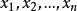 全錯位排列
全錯位排列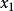 全錯位排列
全錯位排列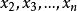 全錯位排列
全錯位排列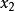 全錯位排列
全錯位排列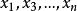 全錯位排列
全錯位排列錯排, 需排在 、 需排在 如此類推。
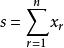 全錯位排列
全錯位排列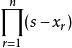 全錯位排列
全錯位排列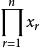 全錯位排列
全錯位排列記 ,錯排結果為 中 的係數
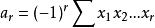 全錯位排列
全錯位排列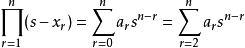 全錯位排列
全錯位排列記 為基本對稱多項式,
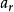 全錯位排列
全錯位排列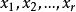 全錯位排列
全錯位排列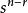 全錯位排列
全錯位排列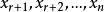 全錯位排列
全錯位排列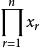 全錯位排列
全錯位排列從 選出 ,然後從 選出 ,組成
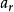 全錯位排列
全錯位排列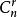 全錯位排列
全錯位排列 全錯位排列
全錯位排列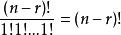 全錯位排列
全錯位排列從 選出r個x有 種可能,從 選出其餘的n-r個x有 種可能
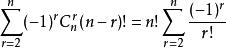 全錯位排列
全錯位排列
