鬆弛法
正文
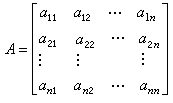
數值計算中解線性代數方程組的一類疊代法。當方程組的未知量個數甚多而又有大量的零係數時,常用這類方法求解。基本疊代格式 設線性代數方程組為
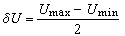 (1)
(1)
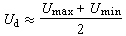 (2)
(2)
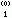 ,x
,x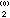 ,…,x
,…,x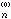 ,就可求出x
,就可求出x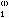 ,x
,x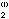 ,…,x
,…,x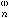 ,由後者又可求出x
,由後者又可求出x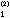 ,x
,x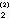 ,…,x
,…,x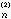 ,如此繼續直到滿足精度要求為止,例如對所有的i,
,如此繼續直到滿足精度要求為止,例如對所有的i,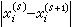 或
或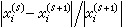 (若
(若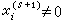 )或剩餘
)或剩餘 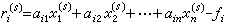
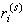 |小於某給定的小數ε時就終止疊代而將
|小於某給定的小數ε時就終止疊代而將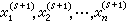 取作方程組(1)的解。疊代格式(2)稱為同時超鬆弛法或JOR法,其中的ω為一實參數,稱為鬆弛因子,當ω=1時就是通常所謂的簡單疊代法,或稱雅可比法。
取作方程組(1)的解。疊代格式(2)稱為同時超鬆弛法或JOR法,其中的ω為一實參數,稱為鬆弛因子,當ω=1時就是通常所謂的簡單疊代法,或稱雅可比法。 若在疊代格式(2)中,將第i個方程疊代出的
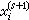 的值代替其後各方程中的
的值代替其後各方程中的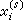 ,就得到疊代格式
,就得到疊代格式 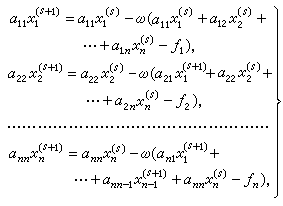 (3)
(3)
 (4)
(4)
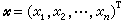 ,
,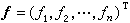 為n維列向量,則(1)可寫為
為n維列向量,則(1)可寫為 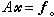 (5)
(5)
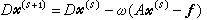 (6)
(6)
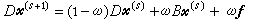 , (7)
, (7)
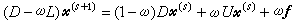 。 (8)
。 (8)
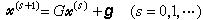 (9)
(9)
ρ(G)<1。
(10)由此可得收斂的一個充分條件為這裡‖G‖是G的任意一‖G‖<1 , (11)
種範數。對上面鬆弛法的疊代格式可以得出一些有關收斂性的命題如下:① 若A為嚴格對角優勢矩陣(見對角優勢矩陣)或不可約弱對角優勢矩陣,|D -1B|為矩陣D -1B的元素取絕對值所成的矩陣,則JOR法和SOR法在
0<ω<2/(1+ρ)|D -1B|範圍內收斂,並且在所述條件下,上式右端是一個大於1的數;
② 若A為埃爾米特矩陣,且αii(i=1,2,…,n)均為正,則JOR法收斂的充分必要條件為A和2ω -1D-A正定;
③ SOR法收斂的必要條件為0<ω<2;
④ 若A為埃爾米特矩陣,αii(i=1,2,…,n)均為正,則SOR法收斂的充分必要條件為A正定和0<ω<2。
鬆弛因子的選取 ω 的值選取得適當可使鬆弛法有較好的收斂性,然而如何選取最優的ω,還是一個困難的問題。通常用五點差分格式解二維二階橢圓型方程得到的線性代數方程組的係數矩陣是塊三對角矩陣,主對角塊是三對角陣,非主對角塊為對角陣。對這種方程組若記簡單疊代和超鬆弛疊代的疊代矩陣為J和Lω,則它們的特徵值λ(J)和λ(Lω)之間有關係
 。 (12)
。 (12)
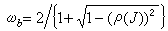 。 (13)
。 (13)
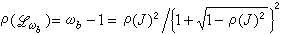 , (14)
, (14)
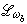 )分別為矩陣J和
)分別為矩陣J和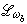 的譜半徑。這些結果還可推廣到所謂“相容次序”的矩陣。儘管如此,在實際計算中仍難以精確確定ωb的值,而往往是通過一些試算或用其他方法先估計ρ(J),再來估計ωb。也可用若干ω值試疊代,從中選取使斂速較快者。從(12)式還可看出,ωb在1與2之間,且從大於ωb的一側選取ω,然後逐步減小,較為有利。
的譜半徑。這些結果還可推廣到所謂“相容次序”的矩陣。儘管如此,在實際計算中仍難以精確確定ωb的值,而往往是通過一些試算或用其他方法先估計ρ(J),再來估計ωb。也可用若干ω值試疊代,從中選取使斂速較快者。從(12)式還可看出,ωb在1與2之間,且從大於ωb的一側選取ω,然後逐步減小,較為有利。 當取ω=1時,由(12)有λ(L1)=(λ(J))2。即對相容次序的矩陣來說,賽德爾疊代比簡單疊代斂速快一倍。在很多情況下,賽德爾疊代比簡單疊代收斂快。實際上,若A =M-N,且A -1、M -1和N的元素均非負,則疊代過程
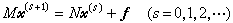 (15)
(15)
此外,若將A分成塊來形成分塊矩陣,而將(6)(7)(8)中的D、B、L和U分別取為A的主對角塊、-A的非主對角塊、下三角塊和上三角塊所形成的矩陣,則疊代(15)的收斂速度可能更快。這樣得出的疊代格式稱為塊鬆弛疊代,相應地有塊簡單疊代,塊超鬆弛疊代等。對照之下,前面的疊代就稱為點鬆弛疊代,上面關於最佳鬆弛因子的討論對塊鬆弛疊代也是適用的。
上述的一些疊代法有時收斂都很慢,這就需要用一些輔助方法來加速收斂,例如半疊代加速、共軛梯度法加速等。
參考書目
馮康等編:《數值計算方法》,國防工業出版社,北京,1978。
D.M.Young,Iterative Solution of large Linear Systems,Academic Press, New York,1971.
R.S.瓦格著,蔣爾雄、游兆永、張玉德譯:《矩陣疊代分析》,上海科學技術出版社,上海,1966。(R.S.Varga,Matrix Iterative Analysis , Prentice - Hall,Englewood Cliffs, New Jersey, 1962.)
