正文
n個變數n個方程(n >1)的方程組表示為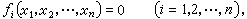 (1)
(1)
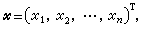 ƒ=
ƒ=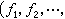
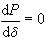 則(1)簡寫為ƒ(尣)=0。若存在尣*∈D,使ƒ(尣*)=0,則稱尣*為非線性方程組的解。方程組(1)可能有一個解或多個解,也可能有無窮多解或無解。對非線性方程組解的存在性的研究遠不如線性方程組那樣成熟,現有的解法也不象線性方程組那樣有效。除極特殊的方程外,一般不能用直接方法求得精確解,目前主要採用疊代法求近似解。根據不同思想構造收斂於解尣*的疊代序列{尣k}(k=0,1,…),即可得到求解非線性方程組的各種疊代法,其中最著名的是牛頓法。
則(1)簡寫為ƒ(尣)=0。若存在尣*∈D,使ƒ(尣*)=0,則稱尣*為非線性方程組的解。方程組(1)可能有一個解或多個解,也可能有無窮多解或無解。對非線性方程組解的存在性的研究遠不如線性方程組那樣成熟,現有的解法也不象線性方程組那樣有效。除極特殊的方程外,一般不能用直接方法求得精確解,目前主要採用疊代法求近似解。根據不同思想構造收斂於解尣*的疊代序列{尣k}(k=0,1,…),即可得到求解非線性方程組的各種疊代法,其中最著名的是牛頓法。 牛頓法及其變形
牛頓法基本思想是將非線性問題逐步線性化而形成如下疊代程式: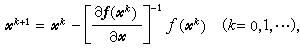 (2)
(2)

這個程式至少具有2階收斂速度。由尣k算到尣k+的步驟為:①由尣k算出ƒ(尣k)及
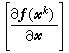 ;②用直接法求線性方程組
;②用直接法求線性方程組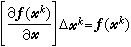 的解Δ尣k;③求
的解Δ尣k;③求 。
。 由此看到疊代一次需計算n個分量函式值和 n2個分量偏導數值,並求解一次n階線性方程組。
為了評價非線性方程組不同疊代法的優劣,通常用效率
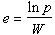 作為衡量標準,其中P為疊代法的收斂階,W為每疊代步計算函式值ƒi及偏導數值
作為衡量標準,其中P為疊代法的收斂階,W為每疊代步計算函式值ƒi及偏導數值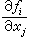 的總個數(每疊代步中求一次逆的工作量相同,均不算在W 內)。效率e越大表示此疊代法花費代價越小,根據效率定義,牛頓法(2)的效率為
的總個數(每疊代步中求一次逆的工作量相同,均不算在W 內)。效率e越大表示此疊代法花費代價越小,根據效率定義,牛頓法(2)的效率為 。
。 牛頓法有很多變形,如當
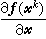 奇異或嚴重病態時,可引進阻尼因子λk,得到阻尼牛頓法,即
奇異或嚴重病態時,可引進阻尼因子λk,得到阻尼牛頓法,即 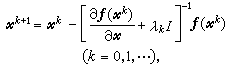
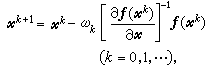 (3)
(3)
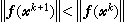 成立。
成立。 為減少解線性方程組次數,提高效率,可使用修正牛頓程式
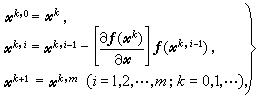 (4)
(4)
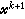 的工作量為W =n2+mn,於是該法的效率
的工作量為W =n2+mn,於是該法的效率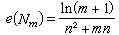 。當n=10,m=7時,
。當n=10,m=7時,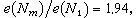 當n=100,m=37時,
當n=100,m=37時,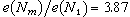 ,由此看到修正牛頓法(4)比牛頓法效率高,且m 越大效果越明顯。
,由此看到修正牛頓法(4)比牛頓法效率高,且m 越大效果越明顯。 在計算機上往往採用不計算偏導數的離散牛頓法,即
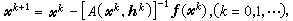 (5)
(5)
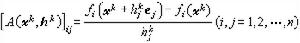 ,
,
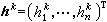 ,若取
,若取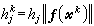 ,則(5)仍具有2階收斂速度。其效率與牛頓法相同。
,則(5)仍具有2階收斂速度。其效率與牛頓法相同。 若在牛頓法(2)中解線性方程組不用直接法,而採用疊代法則得到一類解非線性方程組的雙重疊代法。按解線性方程組採用的方法不同就得到不同名稱的疊代法,如牛頓-賽德爾疊代法,牛頓-sor疊代法,牛頓-ADI疊代法,等等。這些方法都具有超線性收斂速度,工作量也比牛頓法大,除了對某些特殊稀疏方程組外,通常用得校少。若將解線性方程組疊代法的思想直接用於非線性方程組(1),然後把(1)化為一維方程求解,可得到另一類雙重疊代法,由於採用的疊代法與解一維非線性方程的方法不同,則得到不同的雙重疊代法。如果利用SOR疊代法後再用牛頓法解一維方程則得SOR-牛頓疊代法,在牛頓法中只計算一步而不進行疊代,則得一步的SOR-牛頓疊代,其計算公式可表示為
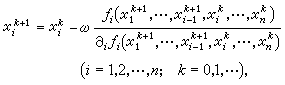
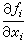 ;ω為疊代參數,當ω=1時就是賽德爾-牛頓疊代法,這類方法對解維數高的稀疏的非線性方程組是有效的。
;ω為疊代參數,當ω=1時就是賽德爾-牛頓疊代法,這類方法對解維數高的稀疏的非線性方程組是有效的。 割線法
若對方程組 (1)線性化時使用插值方法確定線性方程組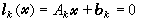 (6)
(6)
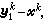
 線性無關,由插值條件可知
線性無關,由插值條件可知 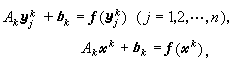
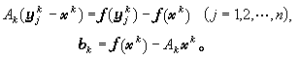
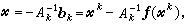 以此作為方程 (1)的新近似,記作
以此作為方程 (1)的新近似,記作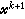 ,於是得到
,於是得到 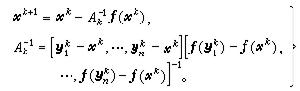 (7)
(7)
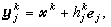
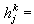
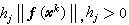 為常數(j=1,2,…,n),就得到與(5)相同的程式,由於它只依賴於尣k點的信息,故也稱一點割線法,若取
為常數(j=1,2,…,n),就得到與(5)相同的程式,由於它只依賴於尣k點的信息,故也稱一點割線法,若取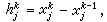 它依賴於點尣k及
它依賴於點尣k及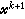 , 稱為兩點割線法。其他多點割線法由於穩定性差,使用較少。
, 稱為兩點割線法。其他多點割線法由於穩定性差,使用較少。 布朗方法
布朗採用對每個分量方程 ƒi(尣)=0逐個進行線性化並逐個消元的步驟,即在每疊代步中用三角分解求線性方程組的解,得到了一個效率比牛頓法提高近一倍的疊代法,即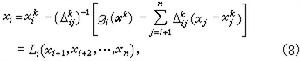
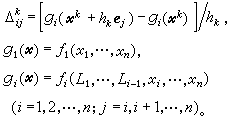
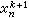 ,再逐次回代,求出
,再逐次回代,求出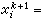
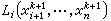 (i=n-1,n-2,…,1)就完成了一個疊代步。布朗疊代程式的斂速仍保持p=2,而每一疊代步的工作量
(i=n-1,n-2,…,1)就完成了一個疊代步。布朗疊代程式的斂速仍保持p=2,而每一疊代步的工作量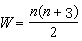 ,故效率
,故效率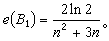 對這方法還可與牛頓法一樣進行改進,得到一些效率更高的算法。這類方法是70年代以來數值軟體包中常用的求解非線性方程組的算法。
對這方法還可與牛頓法一樣進行改進,得到一些效率更高的算法。這類方法是70年代以來數值軟體包中常用的求解非線性方程組的算法。 擬牛頓法
為減少牛頓法的計算量,避免計算雅可比矩陣及其逆,60年代中期出現了一類稱為擬牛頓法的新算法,它有不同的形式,常用的一類是秩1的擬牛頓法,其中不求逆的程式為
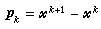 ,
,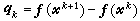 ,
,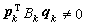 ,稱為逆擬牛頓公式。計算時先給出尣0及 B0,由(9)逐步疊代到滿足精度要求為止。每步只算 n個分量函式值及O(n2)的計算量,比牛頓法一步計算量少得多。理論上已證明,當尣0及B0選得合適時,它具有超線性收斂速度,但實踐表明效率並不高於牛頓法,理論上尚無嚴格證明。
,稱為逆擬牛頓公式。計算時先給出尣0及 B0,由(9)逐步疊代到滿足精度要求為止。每步只算 n個分量函式值及O(n2)的計算量,比牛頓法一步計算量少得多。理論上已證明,當尣0及B0選得合適時,它具有超線性收斂速度,但實踐表明效率並不高於牛頓法,理論上尚無嚴格證明。 最最佳化方法
求方程組 (1)的問題等價於求目標函式為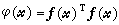 的極小問題,因此可用無約束最最佳化方法求問題(1)的解(見無約束最佳化方法)。
的極小問題,因此可用無約束最最佳化方法求問題(1)的解(見無約束最佳化方法)。 連續法
又稱嵌入法,它可以從任意初值出發求得方程組(1)的一個足夠好的近似解,是一種求出好的疊代初值的方法。連續法的基本思想是引入參數 t∈【0,b】,構造運算元H(尣,t),使它滿足條件:H(尣,0)=ƒ0(尣),H(尣,b)=ƒ(尣),其中ƒ0(尣)=0的解尣0是已知,方程: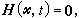 (10)
(10)
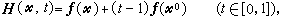 (11)
(11)
H(尣,ti)=0 (i=1,2,…,N) (12)
的解尣i,如果取尣i-1為初值,只要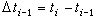 足夠小,牛頓疊代就收斂,但這樣做工作量較大。已經證明,如果方程組(12)只用一步牛頓法,當t=tN=1時,再用牛頓疊代,結果仍具有2階收斂速度。以(11)為例,得到連續法的程式為:
足夠小,牛頓疊代就收斂,但這樣做工作量較大。已經證明,如果方程組(12)只用一步牛頓法,當t=tN=1時,再用牛頓疊代,結果仍具有2階收斂速度。以(11)為例,得到連續法的程式為: 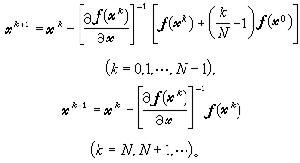
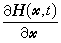 在D×【0,1】嶅R
在D×【0,1】嶅R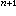 上連續。且
上連續。且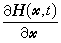 非奇異,則由(10)對t求導可得到等價的微分方程初值問題:
非奇異,則由(10)對t求導可得到等價的微分方程初值問題: 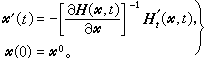 (13)
(13)
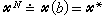 。已經證明只要N足夠大,以尣N為初值再進行牛頓疊代可收斂到方程(1)的解x*,這種算法稱為參數微分法。
。已經證明只要N足夠大,以尣N為初值再進行牛頓疊代可收斂到方程(1)的解x*,這種算法稱為參數微分法。 20世紀60年代中期以後,發展了兩種求解非線性方程組(1)的新方法。一種稱為區間疊代法或稱區間牛頓法,它用區間變數代替點變數進行區間疊代,每疊代一步都可判斷在所給區間解的存在惟一性或者是無解。這是區間疊代法的主要優點,其缺點是計算量大。另一種方法稱為不動點算法或稱單純形法,它對求解域進行單純形剖分,對剖分的頂點給一種恰當標號,並用一種有規則的搜尋方法找到全標號單純形,從而得到方程(1)的近似解。這種方法優點是,不要求ƒ(尣)的導數存在,也不用求逆,且具有大範圍收斂性,缺點是計算量大。