二次型的算術理論
正文
主要研究“以型表型”的問題。設D 是域K或K中含有單位元素1的環，以I記K或D。所謂I上的二次型,是指n個變元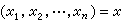
的二次齊次式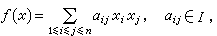 
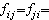
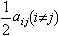而寫
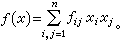此時將ƒ的係數矩陣(ƒij)記為 F，將x視為列矩陣，便有 ƒ＝xTFx，其中xT表x的轉置陣。F的秩nƒ和行列式dƒ,分別稱為型ƒ的秩和行列式。F為滿秩，則稱ƒ為非奇異的；F為降秩，則稱ƒ為奇異的。對給定的I上n元型ƒ和m元型g（m≤n），若存在
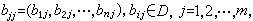使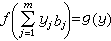
；或者說，當K的特徵非2時存在n×m矩陣B＝（bij），使BTFB=g,其中g是型g的係數矩陣,則稱ƒ可在D上表出型g，且B稱為ƒ表g的一個表法。當m=1時,由ƒ(yb)=g(y)=αy2可得ƒ(b)=α∈I,此時稱ƒ可在D上表出I中元素α。知α求b即所謂以型表“數”。當α=0而b≠0，ƒ非奇異時，則稱ƒ為I上的零型。例如，有理數域上的三元二次型x2+y2-z2是整數環上的零型，且有表法(3,4,5)(商高定理)。當非奇異型ƒ可在I上表出I的所有非零元素時，則稱ƒ為I上的泛型。當m=n時，若型ƒ和g可在D上互相表出，則稱ƒ與g是在D上等價的，記
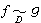。I上諸型可分成若干在D上的等價類。若ƒ與g同類,則nƒ=ng,
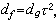τ∈D，簡記為
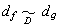；且可在D上表出之型相同。但是，表數相同的型不一定是等價的。 最早對二次型進行系統研究的是C.F.高斯。二次型的算術理論在不定方程中有大量的套用，也套用於組合設計和結晶學。
型的性質與選取型的係數所在的基域K和環D有關。在有理數域Q和p進數域Qp，以及它們包含的整環上所得的結果，大都可以推廣到一般的整體域和局部域上。
域上的二次型 設K是任意一個特徵非2的域，則有以下重要結果：
① K上秩為n的型均在K上等價於一個對角型
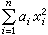式中αi是K中無平方因子的非零元素。 ② E.維特於1936年證明了消去定理：若非奇異l元型
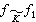，則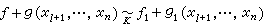
的充分必要條件為
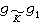。 ③ C.L.西格爾於 1941年證明了K上的零型必為K上的泛型。反之不常真。由此可知，非奇異n元型ƒ可在K上表出K中的元素α的充分必要條件為n+1元型
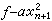是K上的零型。於是把表數問題化為表零問題。 ④ K上非奇異n元型ƒ可在K上表出非奇異m元型g的充分必要條件為存在n-m元型h,使得
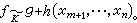當K=C為複數域時,秩為n的型均在C上等價於單位型
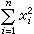，故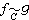
的充分必要條件為nƒ=ng。ƒ為零型的充分必要條件為nƒ≥2。當K=R為實數域時,秩為n的型ƒ均在R上等價於某個形如
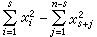的對角型。數s=sƒ，稱為型ƒ的正慣性指標。由消去定理可知,
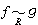的充分必要條件是nƒ=ng,sƒ=sg。通常把s=0或n的型,稱之為定型；s=n的型，稱之為正定型；0<s<n的型，稱之為非定型。ƒ是零型的充分必要條件為 ƒ是非定型。當K=Fq是一個有限域時,秩為n的型均在Fq上等價於某個對角型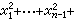
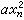,式中α為1或某個非平方數。
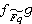的充分必要條件為nƒ=ng,
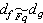;ƒ是零型的充分必要條件為nƒ≥3或nƒ=2而－dƒ是平方數。當K=Qp是p進數域時為判別型在Qp上等價性及表數問題，H.哈塞關於對角型引入了一個重要的符號，即哈塞符號Cp(ƒ)，亦稱哈塞-閔科夫斯基符號。後來,G.帕爾將其推廣為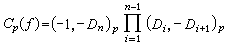 
，Q∞即實數域。(α,β)p由D.希爾伯特於1897年引入，稱為希爾伯特符號，亦記作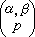
或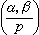
。關於(α,β)p有一套實際算法,因此Cp(ƒ)是可以算出的。利用哈塞符號可以證明，p≠時,Qp上兩個非奇異型
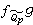的充分必要條件為
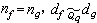,Cp(ƒ)=Cp(g)。Qp上非奇異型ƒ為零型的充分必要條件是:nƒ=2時
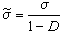；nƒ=3時Cp(ƒ)=1；nƒ=4時
或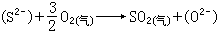
而Cp(ƒ)=1；nƒ≥5。 哈塞於 1923年至1924年建立了關於有理數域Q上型的著名準則。弱哈塞準則，亦稱哈塞－閔科夫斯基定理：Q上兩個非奇異型
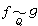的充分必要條件為對所有素數p（包括p=），
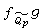。強哈塞準則：Q上非奇異型ƒ是Q上的零型的充分必要條件為對所有素數p（包括p=），ƒ是Qp上的零型。於是Q上的型問題,常可化為Qp上的問題，而Qp上的問題藉助於哈塞符號即可解決。例如，套用Qp上的結果可得到A.邁耶的定理：Q上秩大於4的非定型，均為Q上的零型。對於K是特徵為2的域時,也有少量的研究工作。 環上的二次型 當域K的特徵非2,I=D嶅K是一個環（通常取D使K為其商域）時，設
，
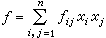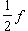為整值型的本原型ƒ稱為非真本原型；否則，稱為真本原型。當非奇異n元整型ƒ可在D上表出m元非奇異整型g，且表法矩陣的所有m階子式的最大公因數為單位數時，則稱此表法是本原的。一般環上的型是極難處理的。例如,當D是非主理想環時,D上的奇異型甚至可能不在D上等價於一個有較少變元的非奇異型。當D=Zp(p≠)時,Zp上的型均在Zp上等價於一個形如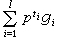
的型，其中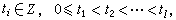
gi是行列式為單位數且無公共變元的整型。當P≠2時,
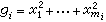是惟一確定的；當p＝2時，gi或是對角型或是形如2x1x2與
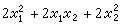的型的直和，此時gi雖不惟一，但l、ti、gi的變元數以及gi之為真本原型或非真本原型卻是不變的。Zp上矩陣為F之非奇異n元整型ƒ可在Zp上表出矩陣為g之非奇異m元整型g的充分必要條件為：存在Z中的n×m矩陣A使得 
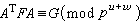成立，此處w=1或3視p為奇素數或2而定,u≥0適合於pu｜dg,pu+1
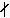dg。當D=Z時，弱哈塞準則不成立。對所有p(包括p=)均在Zp上等價於整型ƒ的全體整型，稱為ƒ的一個族。族中可能包含多個Z上的等價類，此時只能證明：對所有素數p和p＝，若非奇異整型 ƒ 均可在Zp上表出非奇異整型（或非零整數）g,則在ƒ的族中必存在一個可在Z上表出g的整型。因此，當ƒ的族只含一個Z上的等價類時,即可獲得ƒ表型（或數）的解答。M.艾希勒於 1952年引入一種介於Z上的等價類和族之間的分類，即所謂鏇子族,並證明了nƒ≥3的非奇異非定整型ƒ的鏇子族與ƒ的在Z上的等價類重合。非定整型在Z上的等價性問題,可由判定兩型是否同屬一個鏇子族的方法解決。 關於表數問題，G.L.沃森在1955年用初等方法得到了一個很好的結果：nƒ≥4的非奇異的非定整型ƒ可在Z上表出一個非零整數α的充分必要條件是：對所有p（包括p=
），ƒ均可在Zp上表出α。對於正定整型在一般情形下只能證明:若nƒ≥4的正定型ƒ對每個p（包括p=）均可本原地在Zp上表出正整數α,則存在整數N=N(ƒ),當α≥N 時,α可被ƒ本原地在Z上表出;當α<N 時,α可被ƒ的鏇子族中的某個整型本原地在Z上表出。 二次型的簡化法 這是R上的型關於在Z上等價性的理論,由C.埃爾米特首先提出。其基本問題是要從R上諸型的每個Z上的等價類中選出的一個係數儘可能簡單(即滿足某些所謂簡化條件)的型來,這樣的型稱為已化型。簡化方法很多，最常用的是埃爾米特和H.閔科夫斯基的簡化法，它們均與正定二次型 ƒ 的極小值 minƒ 有關，minƒ是型ƒ(x)對於所有非零整向量x的最小值。可以證明，存在一個僅與變元數n有關的常數сn,使得對所有n元正定型ƒ均有
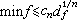。例如,埃爾米特取
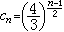。當n≤8時,сn的最佳值rn已於1936年前定出：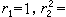
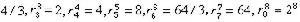,但是n>8時rn的值迄今未解決。關於正定型
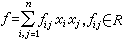，埃爾米特簡化法和閔科夫斯基簡化法分別把適合簡化條件:
+
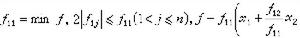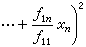是n-1元已化型,和簡化條件：對每個i(1≤i≤n)和所有使 bi,bi+1,…,bn的最大公因數是1的整向量
均有ƒii≤ƒ(b)的型ƒ,稱之為H已化型和M已化型。易知，對M已化型也有ƒ11=minƒ,且可證明簡化條件中的b只需有限個。 埃爾米特還給出了關於非定型的一種簡化法：對給定的非奇異n元非定型g，有多種方法將其表為n個線性無關的實線性型Li(x)的平方的代數和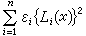 
，εi=±1。對這樣的每種表法，正定型
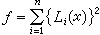稱為 g的一個埃爾米特強函式。若ƒ中有一個是M已化型，則稱非定型 g為H已化型。對二元非定型，有一種基於連分數的簡化法，但是不能推廣到多元的情形。可以證明，R上每個正定型均在Z上等價於至少一個而至多有限個H（或M）已化型;R上每個非定型均在Z上等價於至少一個H已化型；Q上每個非定型均在Z上等價於至多有限個H已化型。對於整型，可以證明,有給定行列式的n元非奇異整型，分別屬於有限個Z上的等價類。因此,族和鏇子族中均只含有限個Z上的等價類。 參考書目
J.W.S. Cassels,rational quadratic Forms,Academic Press,London,1978.
L.E.Dickson,History of the Theory of Numbers,Vol.3, Carnegie Institution of Washington, New York,1952.
B.W.Jones,The Arithmetic Theory of Quadratic Forms,carus Math.Monographs,No.10,Buffalo,1950.
G.L.Watson,Integral Quadratic Forms, Cambridge Univ.Press,London,1960.
