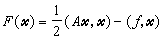簡介
 共軛梯度法
共軛梯度法共軛梯度法最早是由提出來在這個基礎上,Fletcher和Reeves (1964)首先提出了解非線性最最佳化問題的共軛梯度法。由於共軛梯度法不需要矩陣存儲,且有較快的收斂速度和二次終止性等優點,現在共軛梯度法已經廣泛地套用於實際問題中。
共軛梯度法是一個典型的共軛方向法,它的每一個搜尋方向是互相共軛的,而這些搜尋方向d僅僅是負梯度方向與上一次疊代的搜尋方向的組合,因此,存儲量少,計算方便
算法介紹
又稱共軛斜量法,是解線性代數方程組和非線性方程組的一種數值方法,例如對線性代數方程組 Ax=ƒ, (1)式中A為n階矩陣,x和ƒ為n維列向量,當A對稱正定時,可以證明求(1)的解X*和求二次泛函
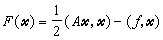 共軛梯度法
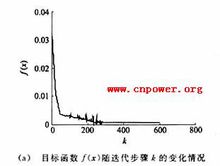
共軛梯度法的極小值問題是等價的。此處(x,у)表示向量x和у的內積。由此,給定了初始向量x(0),按某一方向去求(2)式取極小值的點x(1),就得到下一個疊代值x(2),再由x(2)出發,求x(3)等等,這樣來逼近x*。若取求極小值的方向為F在 x(k=1,2,…)處的負梯度方向就是所謂最速下降法,然而理論和實際計算表明這個方法的收斂速度較慢,共軛梯度法則是在 x(k-1)處的梯度方向r(k-1)和這一步的修正方向p(k-1)所構成的二維平面內,尋找使F減小最快的方向作為下一步的修正方向p(k),即求極小值的方向p(其第一步仍取負梯度方向)。計算公式為
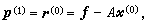 公式
公式再逐次計算
(k=1,2,…)。可以證明當i≠j時,
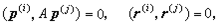 公式
公式從而平p(1),p(2)形成一共軛向量組;r(0),r(1),…形成一正交向量組。後者說明若沒有捨入誤差的話,至多 n次疊代就可得到(1)的精確解。然而在實際計算中,一般都有捨入誤差,所以r(0),r(1),…並不真正互相正交,而尣(0)尣(1),…等也只是逐步逼近(1)的真解,故一般將共軛梯度法作為疊代法來使用。
近來在解方程組(1)時,常將共軛梯度法同其他一些疊代法結合作用。特別是對病態方程組這種方法往往能收到比較顯著的效果。其方法是選取一對稱正定矩陣B並進行三角分解,得B=LLT。將方程組(1)化為 hу=b, (3)
此處y=lTx,b=l-1ƒ,h=l-1Al-T,而
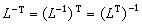 公式
公式再對(3)用共軛梯度法,計算公式為
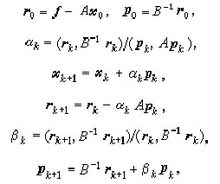 公式
公式k=0,1,2,…)適當選取B,當B很接近A時,h的條件數較之A大大減小,從而可使共軛梯度法的收斂速度大為加快,由一些疊代法的矩陣分裂A=M -N,可選取M 為這裡的B,例如對稱超鬆弛疊代(SSOR),強隱式疊代(SIP)等,這類方法常稱為廣義共軛梯度法或預條件共軛梯度法,它也可用於解代數特徵值問題。