線性代數群
設G是代數閉域K上的代數簇,如果G還具有群的結構，並且群的乘積運算G×G→G與求逆元運算 G→G都是代數簇的態射，那么G稱為K上的代數群。如果G是仿射簇,那么G稱為仿射代數群或線性代數群；如果G是不可約的完備簇,那么G稱為阿貝爾簇。雖然代數群的定義與拓撲群的定義十分相似，但是代數簇的積不是拓撲積而是扎里斯基積，所以一般地說，代數群不是拓撲群。代數群的同態是兼為群的同態與代數簇的態射的一個映射；同構概念由此自然得出。易知，代數群的閉子群也是代數群。代數群的同態像是閉的，所以也是代數群。代數群關於它的正規閉子群的商群也是代數群。對任意代數群G,總可以惟一找到一個正規的仿射子群N,使G/N是阿貝爾簇。因此,代數群的研究主要是線性代數群與阿貝爾簇的研究。阿貝爾簇的研究屬於代數幾何範疇，阿貝爾簇的群結構很簡單（都是阿貝爾群），而且被簇結構惟一確定（簇同構的兩個阿貝爾簇一定同構）。線性代數群的研究則更多是按代數學觀點進行，而成為與李群理論相平行的一個獨立學科。
線性代數群理論的萌牙，可以追溯到19世紀末葉。當時L.毛瑞爾與(C.-)É.皮卡實際上已經研究了複數域上的線性代數群；皮卡把這些群用到線性微分方程的伽羅瓦理論中去。但是，在此後的半個世紀中，他們的這一工作並未引起人們的注意，而É.(-J.)嘉當與（C.H.）H.外爾在這期間對李群與李代數進行了深入的研究，所獲成果促進了線性代數群理論的正式出現。20世紀40年代，C.謝瓦萊與段學復用李代數的方法，討論了特徵為零的任意域上的線性代數群，這是線性代數群理論誕生的前奏。1955年前後，線性代數群的一般理論終於由A.博雷爾與謝瓦萊等人提出來了。而後經博雷爾、R.施坦伯格和J.蒂茨等人的進一步發展，形成了一個較完美的數學體系，並對基礎數學的許多領域諸如半單李群及其算術子群、典型群、有限單群、不變數理論等的發展起了重要的作用。
K的加法群Gα；K的乘法群Gm；K上所有n×n的非奇異矩陣在矩陣乘法上所成的群GL(n,K)，即所謂K上的n次一般線性群；GL(n,K)中由行列式為1的矩陣組成的子群SL(n,K),即所謂K上的n次特殊線性群；GL(n,K)的其他閉子群等等都是線性代數群的例子，而且它們已具有相當的普遍性。任一線性代數群必同構於某個一般線性群的某個閉子群，這就是“線性代數群”這個術語的由來。以下均用G代表一個線性代數群。
把G嵌入為GL(n，K)的閉子群後，每個x∈G可以在GL(n,K)中進行若爾當分解:在GL(n,K)中有惟一的一對元素s與u，使得：①s為半單元(即可對角化的元素),u為冪麼元（即所有特徵根都是1的元素）；②su=x=us。可以證明s與u都在G中,而且G 的元素的這種分解與G到GL(n,K)的嵌入無關。於是,在G中就定義了半單元、冪麼元與若爾當分解的概念。
僅由半單元組成的連通、交換的線性代數群稱為環面；僅由冪麼元素組成的線性代數群稱為冪麼群。環面與冪麼群都是可解的，甚至是冪零的。更一般地說，任何連通可解線性代數群 B總可寫成它的一個極大環面子群與它的極大冪么子群的半直積，其中極大冪么子群含有B的所有冪麼元，從而是正規的;若且唯若這個半直積是直積時，B是冪零群。
G的極大連通可解子群稱為 G的博雷爾子群。G的所有博雷爾子群（對應地，極大環面子群、極大連通冪么子群）都在G中共軛；如果G是連通的,那么G的任一元素(對應地，半單元、冪麼元)一定在某個博雷爾子群（對應地,極大環面子群、極大連通冪么子群）中。此外,G的環面子群的正規化子對中心化子的指數是有限的。
G有惟一的最大正規連通可解子群R(G)，它稱為G的根基；G還有惟一的最大正規連通冪么子群Ru(G)，它稱為G的冪麼根基。顯然,Ru(G)由R(G)中所有冪麼元組成。
如果Ru(G)是平凡的，就稱G為簡約線性代數群；如果G是連通的，且R(G)是平凡的，就稱G為半單線性代數群。例如,GL(n,K)是簡約的，而SL(n,K)是半單的。因為對任意連通線性代數群來說,G/R(G)總是半單的,R(G)的結構又比較簡單，所以線性代數群理論的中心問題之一，是半單群的結構與分類。為敘述這方面的結果，首先介紹G的李代數與根系，並在以下假定G是連通的。
設K【G】為簇G到K的正則函式組成的K代數,則G以兩種方式自然地作用在K【G】上：對所有x、y∈G,ƒ∈K【G】，定義(λxƒ)(y)=ƒ(x-1y)，(ρxƒ)(y)=ƒ(yx)。這兩種作用分別稱為左平移與右平移。
K線性映射x:K【G】→K【G】如果滿足
x(ƒg)=x(ƒ)g+ƒx(g)，
就稱為K【G】的K導子;如果x還與所有的λx(x∈G)可換,就稱x為K【G】的左不變K導子。如果x、Y都是左不變K導子，那么它們的任意K線性組合以及它們的換位子【x,Y】=x。Y-Y。x仍是左不變K導子。所以K【G】的左不變K導子全體組成K上的一個李代數g，它稱為G的李代數。作為向量空間，g可以等同於G在恆等元處查里斯基切空間。如果x∈g,x∈G，那么
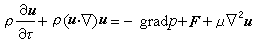於是得到G在g上的伴隨表示Ad:G→GL(g)。特別,把G嵌入為GL(n,K)的閉子群後，g是gL(n,K)（由K上所有n×n矩陣組成的李代數）的子代數。此時,G在g上的伴隨作用就是矩陣的共軛。 固定G 的一個極大環面子群T，令H(T)為T到Gm的代數群同態全體,則H(T)是K【T】的單位元乘法群的子群。但是改用加法來記H(T)的群運算，並把它的元素稱為T的特徵標。設G是連通簡約群,α是T的非零特徵標，並且有非零向量x∈g,使得對所有t∈T都有Ad(t)x=α(t)x，則稱α為G關於T的根。G關於T的根的全體φ =φ(G，T)滿足抽象根系的所有公理,它稱為G關於T的根系。它的外爾群同構於T的正規化子對中心化子(=T)的商群W =W(G,T)。由於從不同的極大環面得出的根系是同構的，有時就把φ 簡稱為G的根系，把W 簡稱為G的外爾群。
如果B是含T的博雪爾子群,那么W可以作為G關於(B，B)的雙陪集分解的代表元系，即
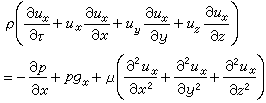,且是不相交的並。G的這個雙陪集分解稱為布魯哈特分解。特別，由W 中最長的元素w0所代表的雙陪集Bw0B是G的稠密開集，稱為G的大胞腔。 如果G是半單的,那么H(T)含在φ生成的歐氏空間中，而且是Ф的根格Hr與權格Hw之間的一個格。半單線性代數群的分類定理斷言:K上的半單線性代數群的同構類與二元組(φ,H)的同構類一一對應,這裡φ是一個抽象根系，H是Hr與Hw之間的任意一個格。更確切地說，給定這樣一個二元組,必有惟一的(在同構意義下)K上的半單線性代數群G(φ,H),使得G的根系同構於φ,在此同構下,G的極大環面的特徵標群就是H。此外,若H1吇H2,則有典範的代數群滿同態
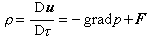。因此，G(φ,Hw)覆蓋了K上所有具有根系φ 的半單線性代數群，這個群稱為普遍型的或單連通的；G(φ,Hr)被K上所有具有根系φ 的半單線性代數群覆蓋，這個群稱為伴隨型的。 如果φ 是不可約根系，那么G(φ，H)稱為殆單群。這是由於G(φ,H)的任一正規真子群都是有限的與中心的之故。特別,G(φ,Hr)是一個單群。由根系的分類定理知,殆單群有Al，Bl，Cl，Dl四個無限系列和E6,E7，E8,F4，G2五個例外類型。例如,SL(n,K)就是An-1型的單連通群。當φ可約時,φ的每一個不可約分支φi對應G＝G(φ,H)的一個殆單正規子群Gi，所有這些Gi的直積到G的典範同態是滿的,它的核是有限的與中心的。這些Gi稱為G的殆單分支。如果殆單群不是例外類型的群,就稱為典型群。
當K=C是複數域時,G(φ,H)在普通復拓撲下是個具有根系φ 的復半單李群。所以線性代數群理論可以看作李群理論的一個推廣。
線性代數群理論還與有限單群的理論有密切聯繫。設K是具有素特徵p的域,Fq是q=pr個元素的有限域。如果K上的線性代數群G具有Fq結構,即K【G】可以寫成一個Fq子代數Fq【G】與K的張量積，而且由G的乘積運算與求逆元運算導出的K代數同態
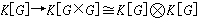與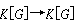
可以限制為Fq代數同態
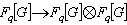與Fq【G】→Fq【G】,那么，把Fq【G】的每個元素q次方得到的K代數同態K【G】→K【G】導出一個代數群同態F：G→G，它稱為G的弗羅貝尼烏斯同態,其不動點G< sup>就是一個有限群。當G是半單群時,G< sup>稱為有限謝瓦萊群或有限李型群。特別，當G 是單群時，除極少數例外，G< sup>都是有限單群。這類有限單群稱為李型單群。從有限單群的分類定理知，除素數階循環群與交錯群外，所有含在某個無限序列中的單群都是李型單群。例如，把SL(n,K)中的矩陣的每個元素q次方，便得到SL（n，K）的一個弗羅貝尼烏斯同態,其不動點子群為Fq上的n次特殊線性群SL(n,q)；同樣的弗羅貝尼烏斯同態作用在An-1型伴隨群pSL(n,K)上，得到的不動點子群便是李型單群pSL(n, q)。又如，由
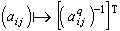（T表示轉置）定義的SL(n,K)的弗羅貝尼烏斯同態的不動點子群則是酉群SU(n,q2)。 參考書目
A.Borel,Lineαr Algebrαic Groups, Benjamin, New York, 1969. J.E.Humphreys,Lineαr Algebrαic Grαups,Grαduαte Text in Mathematics 21, Springer-Verlag, Berlin,1975.
