定義
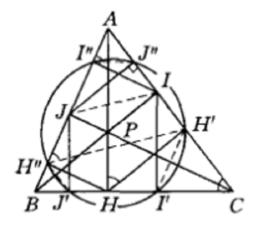
三角形每邊上高的垂足在另兩邊上的射影共六點在同一圓周上,這圓稱為三角形的泰勒圓(Taylor's circle) 。
證明過程
 泰勒圓
泰勒圓 泰勒圓
泰勒圓 泰勒圓
泰勒圓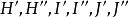 泰勒圓
泰勒圓設三條高的垂足分別為,它們在另兩條邊上的射影分別為,作圖如下。
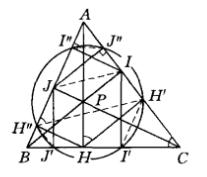 圖1
圖1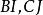 泰勒圓
泰勒圓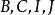 泰勒圓
泰勒圓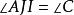 泰勒圓
泰勒圓因為是高,所以四點共圓,得。
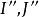 泰勒圓
泰勒圓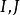 泰勒圓
泰勒圓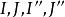 泰勒圓
泰勒圓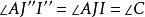 泰勒圓
泰勒圓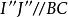 泰勒圓
泰勒圓因為分別為的射影,所以四點共圓,得,從而有。
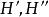 泰勒圓
泰勒圓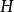 泰勒圓
泰勒圓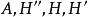 泰勒圓
泰勒圓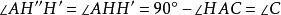 泰勒圓
泰勒圓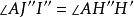 泰勒圓
泰勒圓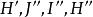 泰勒圓
泰勒圓由於是的射影,所以四點共圓,,於是,推得四點共圓。
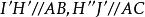 泰勒圓
泰勒圓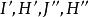 泰勒圓
泰勒圓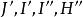 泰勒圓
泰勒圓同理可得,,以及四點共圓和四點共圓。
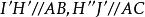 泰勒圓
泰勒圓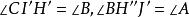 泰勒圓
泰勒圓由,得。
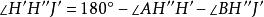 泰勒圓
泰勒圓而
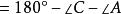 泰勒圓
泰勒圓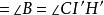 泰勒圓
泰勒圓,
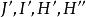 泰勒圓
泰勒圓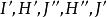 泰勒圓
泰勒圓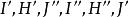 泰勒圓
泰勒圓因而四點共圓,故五點共圓,進而得六點共圓 。