沃爾什逼近
正文
在基本區間【0,1)上它們的定義如下:φ0(x)=1,若0≤x<1/2;φ0(x)=-1,若1/2≤x<1。對任一自然數n,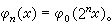 容易看出,對每個n,φn(x)在【0,1)的2
容易看出,對每個n,φn(x)在【0,1)的2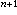 個等分區間上交錯地取值1與-1。沃爾什函式系是拉德馬赫爾函式系的完備化,首先由美國數學家J.L.沃爾什於1923年給出。如果把自然數n依二進表示為
個等分區間上交錯地取值1與-1。沃爾什函式系是拉德馬赫爾函式系的完備化,首先由美國數學家J.L.沃爾什於1923年給出。如果把自然數n依二進表示為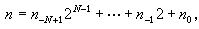 其中
其中 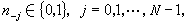
w 0(x)=1, 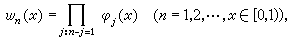
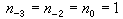 ,而有
,而有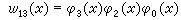 。在工程上常用列率序的沃爾什函式。為此需要數的格雷碼。設對集{0,1}引用偽加運算如下:
。在工程上常用列率序的沃爾什函式。為此需要數的格雷碼。設對集{0,1}引用偽加運算如下: 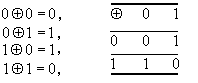
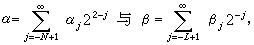
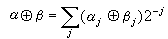 ,這裡求和由-N +1與-L+1中較小者開始。一個自然數
,這裡求和由-N +1與-L+1中較小者開始。一個自然數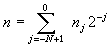 的二進代碼是(n_N+1,…,n-1,n0),它的格雷碼G(n)便是
的二進代碼是(n_N+1,…,n-1,n0),它的格雷碼G(n)便是 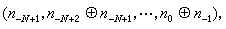
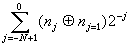 ,這裡約定 n-N=0。反之,如果知道了自然數 k的格雷碼
,這裡約定 n-N=0。反之,如果知道了自然數 k的格雷碼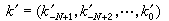 ,則原來的數k的二進代碼是
,則原來的數k的二進代碼是 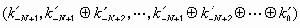 。
。
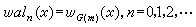 。利用格雷反碼G -1(k),自然有
。利用格雷反碼G -1(k),自然有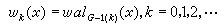 。在數學討論中以系{wk(x)}為便,但在工程上則以列率序為便。下面列舉依列率序的沃爾什函式系的一些性質。
。在數學討論中以系{wk(x)}為便,但在工程上則以列率序為便。下面列舉依列率序的沃爾什函式系的一些性質。 ① 乘法公式 對任意k, j=0,1,2,…有
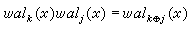 。
。
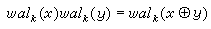 (k=0,1,…)。
(k=0,1,…)。
④ 函式系{wαlk(x)}k=0,1,…構成【0,1)上的一個完備的標準正交系。
⑤ 函式系{wαlk(x)}k=0,1,…構成一個可換群。系中對每個n=0,1,…,前2n個函式{wαl0(x),wαl1(x),…,wαl
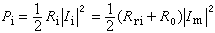 (x)}構成可換子群。
(x)}構成可換子群。 可將這些性質與正弦餘弦函式相比較。正是由於性質④,每個以1為周期的可積函式,都有沃爾什-傅立葉展開式:
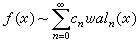 ,
,
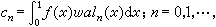 它們稱為ƒ(x)的沃爾什-傅立葉係數。如果用S
它們稱為ƒ(x)的沃爾什-傅立葉係數。如果用S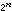 (x)表示展開式的首2n項部分和,那么,在區間【0,1)上幾乎處處有收斂關係
(x)表示展開式的首2n項部分和,那么,在區間【0,1)上幾乎處處有收斂關係 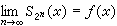 。
。
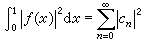 ,
,
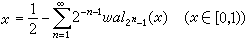 。
。
對任意整數 p>2,可以討論一般的 p進沃爾什函式。還可以引進廣義沃爾什函式與沃爾什-傅立葉變式。此外,如果引進所謂邏輯導數,就容易給出簡單的沃爾什-傅立葉變式表。
設複數Aj=Aj(p), j=0,1,…, p-1由公式
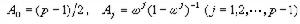
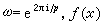 在定義於 【0,∞)上的復值函式。若在這區間上一點x處,和
在定義於 【0,∞)上的復值函式。若在這區間上一點x處,和 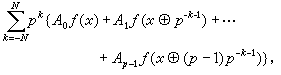
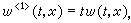
參考書目
鄭維行、蘇維宜、任福賢著:《沃爾什函式理論與套用》,上海科學技術出版社,上海,1983。
鄭維行、蘇維宜: Walsh分析與逼近運算元,《數學進展》,第12卷,第2期,1983。