定義
設
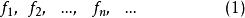 極限函式
極限函式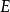 極限函式
極限函式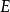 極限函式
極限函式是一列定義在同一數集 上的函式,稱為定義在 上的函式列。
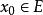 極限函式
極限函式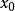 極限函式
極限函式設 ,以 代入(1)可得數列
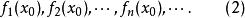 極限函式
極限函式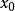 極限函式
極限函式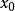 極限函式
極限函式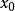 極限函式
極限函式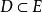 極限函式
極限函式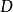 極限函式
極限函式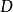 極限函式
極限函式 極限函式
極限函式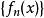 極限函式
極限函式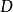 極限函式
極限函式 極限函式
極限函式若數列(2)收斂,則稱函式列(1)在點 收斂, 稱為函式列(1)的收斂點。若數列(2)發散,則稱函式列(1)在點 發散。若函式列(1)在數集 上每一點都收斂,則稱(1)在數集 上收斂。這時 上每一點 ,都有數列 的一個極限值與之相對應,由這個對應法則所確定的 上的函式,稱為(1)的 極限函式 。若把此極限記作 ,則有
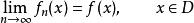 極限函式
極限函式或
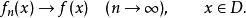 極限函式
極限函式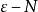 極限函式
極限函式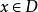 極限函式
極限函式 極限函式
極限函式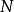 極限函式
極限函式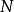 極限函式
極限函式 極限函式
極限函式 極限函式
極限函式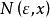 極限函式
極限函式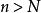 極限函式
極限函式函式列極限的 定義是:對每一固定的 ,任給正數 ,恆存在正數 (注意:一般說來 值的確定與 和 的值都有關,所以也用 表示它們之間的依賴關係),使得當 時,總有
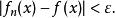 極限函式
極限函式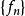 極限函式
極限函式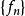 極限函式
極限函式使函式列 收斂的全體收斂點集合,稱為函式列 的收斂域。
套用
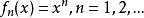 極限函式
極限函式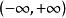 極限函式
極限函式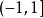 極限函式
極限函式例1 設 為定義在 上的函式列,證明它的收斂域是 ,且有極限函式
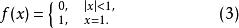 極限函式
極限函式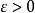 極限函式
極限函式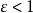 極限函式
極限函式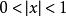 極限函式
極限函式證 任給 (不妨設 ),當 ,由於
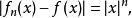 極限函式
極限函式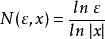 極限函式
極限函式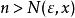 極限函式
極限函式只要取 ,當 時,就有
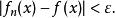 極限函式
極限函式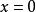 極限函式
極限函式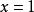 極限函式
極限函式 極限函式
極限函式當 和 時,則對任何正整數 ,都有
 極限函式
極限函式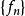 極限函式
極限函式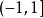 極限函式
極限函式這就證得 在 上收斂,且有(3)式所表示的極限函式。
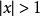 極限函式
極限函式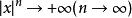 極限函式
極限函式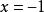 極限函式
極限函式當 時,則有 ,當 時,對應的數列為
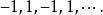 極限函式
極限函式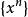 極限函式
極限函式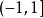 極限函式
極限函式它顯然是發散的. 所以函式列 在區間 外都是發散的。
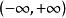 極限函式
極限函式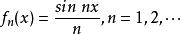 極限函式
極限函式 極限函式
極限函式例 2 定義在 上的函式列。 由於對任何實數 ,都有
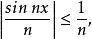 極限函式
極限函式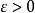 極限函式
極限函式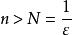 極限函式
極限函式故對任給的 ,只要 ,就有
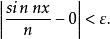 極限函式
極限函式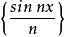 極限函式
極限函式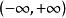 極限函式
極限函式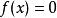 極限函式
極限函式所以函式列 的收斂域為無限區間 ,極限函式 。
