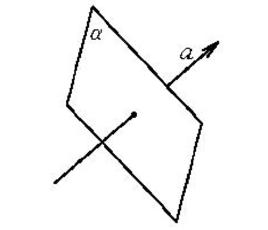
法方程矢式
 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面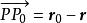 有向平面
有向平面 有向平面
有向平面設為平面上一個已知點,為上任意點, n為的一個法矢(此時成為 有向平面),因和 n垂直,的矢方程可以寫成
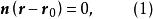 有向平面
有向平面若取平行於 n的一個麼矢 n代替 n,則得
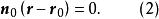 有向平面
有向平面 有向平面
有向平面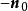 有向平面
有向平面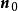 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面這個方程叫做 有向平面 的法方程,取 代也得的一個法方程,不過有向平面的正負側顛倒了。
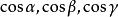 有向平面
有向平面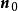 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面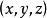 有向平面
有向平面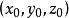 有向平面
有向平面若為的方向餘弦,和的直角坐標依次是和,則(2)寫成坐標式為
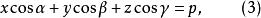 有向平面
有向平面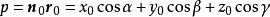 有向平面
有向平面其中。
法方程中係數的幾何意義
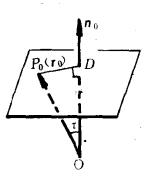 圖2(1)
圖2(1)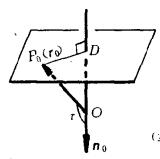 圖2(2)
圖2(2) 有向平面
有向平面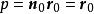 有向平面
有向平面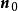 有向平面
有向平面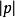 有向平面
有向平面 有向平面
有向平面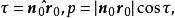 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面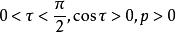 有向平面
有向平面 有向平面
有向平面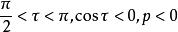 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面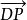 有向平面
有向平面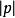 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面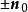 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面 有向平面
有向平面變數係數為有向平面的麼法矢的分量或法矢的方向餘弦已如上述,現在再看(3)的右邊常數項p的幾何意義。因為在上的投影代數長,就是原點與間的距離,令當原點在上時,p=0;當原點在的負側時,(參看圖2(1));當原點在的正側時, (參看圖2(2))。因此,p是到原點的 有向距離DO(平面和點P之間的距離若是|DP|,D是P在上的垂足,則有向距離為DP,當與 n同向,DP>0,反向則DP<0),是和原點間的距離。不難看出,選擇的麼法矢為之一就是選擇的正側,習慣上這樣選擇的正向,使原點在的負側,其目的使p總大於0 。