基礎介紹
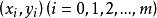 擬合曲線
擬合曲線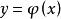 擬合曲線
擬合曲線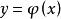 擬合曲線
擬合曲線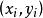 擬合曲線
擬合曲線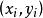 擬合曲線
擬合曲線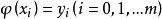 擬合曲線
擬合曲線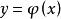 擬合曲線
擬合曲線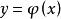 擬合曲線
擬合曲線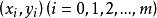 擬合曲線
擬合曲線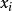 擬合曲線
擬合曲線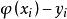 擬合曲線
擬合曲線對於平面上給定的點 ,要尋找y與x之間的近似函式關係 ,插值法要求曲線 準確通過每個給定點 ;而m較大時無論是高次插值還是分段低次插值都將很複雜,數據 一般是由實驗觀測得到的,總會帶有觀測誤差,刻意要求 並不能反映真實的函式關係,反而會引起 的波動加劇,因此用 近似描述已知數據 ,不必要求在每個點處,誤差 ,都為0,只需在所有點處的某種總體誤差最小即可,這就是所謂的 曲線擬 合問題,亦稱為 離散函式最佳平方逼近問題。
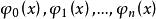 擬合曲線
擬合曲線設給定基函式 ,我們在集合
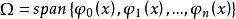 擬合曲線
擬合曲線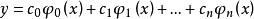 擬合曲線
擬合曲線中尋求形如 的函式,使其近似已知數據。
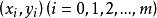 擬合曲線
擬合曲線定義1 對給定的數據 ,若
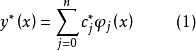 擬合曲線
擬合曲線使得
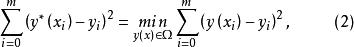 擬合曲線
擬合曲線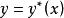 擬合曲線
擬合曲線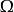 擬合曲線
擬合曲線則稱 為曲線族中的最小二乘擬合曲線,並稱
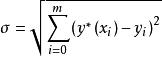 擬合曲線
擬合曲線為均方誤差。
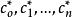 擬合曲線
擬合曲線要確定擬合曲線(1)中的待定係數 ,由(2)式知,就是求多元函式
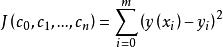 擬合曲線
擬合曲線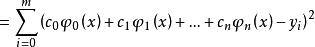 擬合曲線
擬合曲線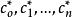 擬合曲線
擬合曲線的最小值點(),由多元函式取極值的必要條件,有
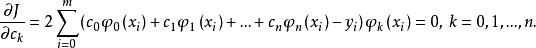 擬合曲線
擬合曲線從而有
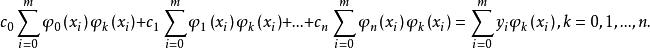 擬合曲線
擬合曲線這是n+1個方程、n+1個未知數的線性方程組,藉助矩陣運算,可寫成如下矩陣形式:
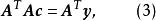 擬合曲線
擬合曲線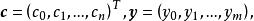 擬合曲線
擬合曲線其中, 而
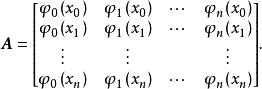 擬合曲線
擬合曲線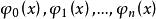 擬合曲線
擬合曲線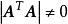 擬合曲線
擬合曲線方程組(3)稱為法方程組,設 線性無關(且滿足Haar條件),則行列式 ,線性方程組(3)存在唯一的一組解。
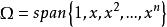 擬合曲線
擬合曲線若取基函式 ,法方程的係數矩陣顯然非奇異,此時一般稱為多項式擬合,求解法方程組,得到擬合係數
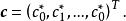 擬合曲線
擬合曲線從而得到
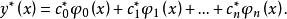 擬合曲線
擬合曲線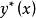 擬合曲線
擬合曲線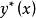 擬合曲線
擬合曲線再由多元函式取極值的充分條件可證明,這樣求出的 確實是方程組(2)的解,即 為最小二乘擬合曲線。
幾種具體的擬合曲線類型
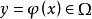 擬合曲線
擬合曲線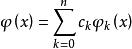 擬合曲線
擬合曲線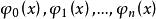 擬合曲線
擬合曲線以上討論的都是線性最小二乘擬合問題,即擬合曲線 ,也就是 是基函式 的線性組合,有些問題雖然數學模型不是線性模型,但通過變換可化為線性模型,則上述最小二乘擬合方法仍然可用。
指數函式擬合
選取擬合函式為指數函式
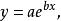 擬合曲線
擬合曲線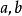 擬合曲線
擬合曲線為待定常數,
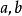 擬合曲線
擬合曲線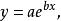 擬合曲線
擬合曲線這是一個關於 的非線性模型,現通過適當變換將其化為線性模型,為此對 兩邊取對數,有
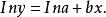 擬合曲線
擬合曲線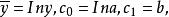 擬合曲線
擬合曲線令於是
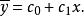 擬合曲線
擬合曲線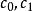 擬合曲線
擬合曲線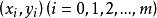 擬合曲線
擬合曲線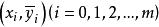 擬合曲線
擬合曲線這是一個關於 的線性模型,原來的已知數據 經取對數後變成一組新數據 ,這裡
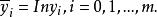 擬合曲線
擬合曲線 擬合曲線
擬合曲線對這組新數據,求形如 的擬合曲線。
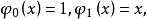 擬合曲線
擬合曲線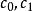 擬合曲線
擬合曲線 擬合曲線
擬合曲線取基函式 則由(3)式可得法方程組,求解出 後即得到擬合曲線 ,從而得到
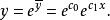 擬合曲線
擬合曲線冪函式擬合
選取擬合函式為冪函式
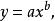 擬合曲線
擬合曲線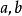 擬合曲線
擬合曲線為待定常數,
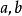 擬合曲線
擬合曲線這也是關於 的非線性模型.兩邊取對數,同樣可將其化為線性模型,即
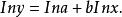 擬合曲線
擬合曲線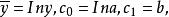 擬合曲線
擬合曲線令 則擬合曲線為
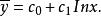 擬合曲線
擬合曲線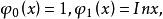 擬合曲線
擬合曲線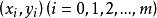 擬合曲線
擬合曲線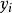 擬合曲線
擬合曲線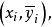 擬合曲線
擬合曲線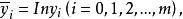 擬合曲線
擬合曲線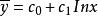 擬合曲線
擬合曲線這時基函式為將原數據中的取對數,得新數據其中對此新數據,用擬合即可。
雙曲型擬合
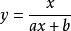 擬合曲線
擬合曲線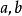 擬合曲線
擬合曲線雙曲型 也是關於 的非線性擬合模型,作變形
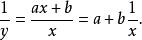 擬合曲線
擬合曲線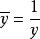 擬合曲線
擬合曲線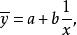 擬合曲線
擬合曲線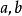 擬合曲線
擬合曲線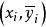 擬合曲線
擬合曲線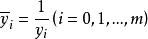 擬合曲線
擬合曲線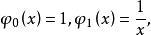 擬合曲線
擬合曲線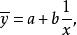 擬合曲線
擬合曲線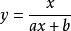 擬合曲線
擬合曲線令 ,則擬合曲線為化成了關於 的線性擬合模型,這時新數據為 ,其中 。基函式為由法方程組(3)即可求出擬合曲線進而求出擬合曲線。

