正文
設動力體系為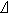
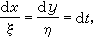 (1)
(1)
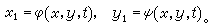 (2)
(2)
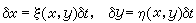 (3)
(3)
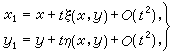 (4)
(4)
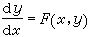 (5)
(5)
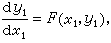 (6)
(6)
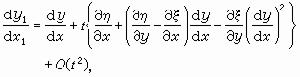
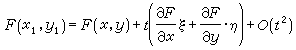 (7)
(7)
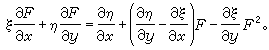 (8)
(8)
利用(8),對已給的 ζ、η,亦即已給的群 (2),可以決定最一般的F(x,y),使方程(5)在群(2)之下不變。當 ζ、η、F一起滿足(8)時,若令
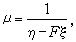 則 (8)便可改寫為
則 (8)便可改寫為 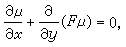 (9)
(9)
特別,在平移群x1=x+t,y1=y(此時ζ=1,η=0,由(8)可解出F=ƒ(y))之下為不變的方程(5)取
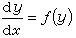
在均勻放大群x1=kx,y1=ky(令k=et即見ζ=x,η=y)之下為不變的方程(5)是齊次方程
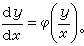 這一事實由齊次方程通解具有形式
這一事實由齊次方程通解具有形式 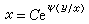 也可清楚地看出。又由(9)知此時上述齊次方程有積分因子
也可清楚地看出。又由(9)知此時上述齊次方程有積分因子 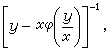
利用這種方法就可看出,許多方程之所以能用初等積分法求解,都是因為使它們不變的變換群(2)是一些易於求解的方程(1)的解。
從理論上講,(1)的通積分可表為
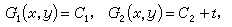 (10)
(10)
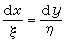 積分而得,故不含 t。設 t=0對應於由(10)所確定的變換群的恆等變換,即知變數代換u=G1(x,y),υ=G2(x,y)能把群(10)化為平移群
積分而得,故不含 t。設 t=0對應於由(10)所確定的變換群的恆等變換,即知變數代換u=G1(x,y),υ=G2(x,y)能把群(10)化為平移群 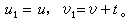
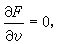 從而方程(5)也就成為可積方程
從而方程(5)也就成為可積方程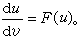
因此,如果對於已給的方程(5)能找到使它不變的變換群(2),就可以取(1)的前一個首次積分中的G1(x,y)=u以代替y而使(5)成為可積方程。例如方程
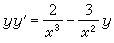 (11)
(11)
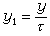 之下不變。 令τ=et可知x1=xet,y1=ye-t是
之下不變。 令τ=et可知x1=xet,y1=ye-t是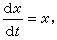
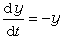 的解。而此方程有一首次積分為xy=C,亦即xy是變換x1=τx,y1=y/τ之下的不變數。取u=xy為新的未知函式以代y,則(11)便化為可以分離變數的方程xuu┡=u2-3u+2。
的解。而此方程有一首次積分為xy=C,亦即xy是變換x1=τx,y1=y/τ之下的不變數。取u=xy為新的未知函式以代y,則(11)便化為可以分離變數的方程xuu┡=u2-3u+2。 以上的方法也可用於高階方程的降階,例如方程
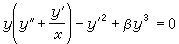 (12)
(12)
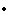
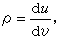 則(12)被化為第二類阿貝爾方程
則(12)被化為第二類阿貝爾方程 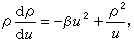 它顯然可化為線性方程求積而得
它顯然可化為線性方程求積而得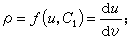 再積分,最後可得(12)的通解為
再積分,最後可得(12)的通解為 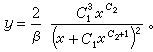
此外,值得一提的是M.S.李、(C.-)É.皮卡等將變換群理論用於線性變係數齊次方程
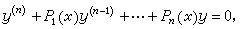
參考書目
J. M. Hill, Solution of Differential Equations by Means of One Parameter Groups,Research Notes in Math., 63, 1982.