簡介
命名來歷
希爾伯特變換是以著名數學家大衛·希爾伯特(David Hilbert)來命名。
定義
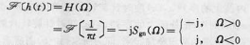圖1希爾伯特變換(hilbert transform) 一個連續時間信號x(t)的希爾伯特變換等於該信號通過具有衝激回響h(t)=1/πt的線性系統以後的輸出回響x(t)。由於h(t)的傅立葉變換為如圖1.
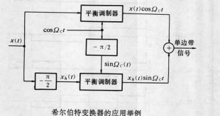圖2所以信號經希爾伯特變換後，在頻域各頻率分量的幅度保持不變，但相位將出現90°相移。即對正頻率滯後π/2，對負頻率導前π/2，因此希爾伯特變換器又稱為90°移相器。圖中所示就是在通信系統中利用直接相移法產生單邊帶信號的方塊圖。圖中x(t)表示輸入信號，相移是通過希爾伯特變換器來實現的。用希爾伯特變換描述幅度調製或相位調製的包絡、瞬時頻率和瞬時相位會使分析簡便，在通信系統中有著重要的理論意義和實用價值。在通信理論中，希爾伯特變換是分析信號的工具，在數位訊號處理中，不僅可用於信號變換，還可用於濾波，可以做成不同類型的希爾伯特濾波器。
在數學與信號處理的領域中，一個實值函式的希爾伯特變換(Hilbert transform)——在此標示為H——是將信號s(t)與1/(πt)做卷積，以得到s'(t)。因此，希爾伯特變換結果s'(t)可以被解讀為輸入是s（t）的線性時不變系統(linear time invariant system)的輸出，而此系統的脈衝回響為1/(πt)。這是一項有用的數學，用在描述一個以實數值載波做調製的信號之複數包絡(complex envelope)，出現在通訊理論中發揮著重要作用。
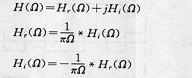圖3理論證明，一個物理可實現的系統，由於因果性的制約(h(t)=O，t<0)其系統函式的實部H(Ω)與虛部h（Ω)互為一對希爾伯特變換，或者說存在著希爾伯特變換的關係如圖3
式中H(Ω)是h(t)的傅立葉變換，Ω表示角頻率，所以，已知H(Ω)，則H(Ω)就唯一地被確定，反之也一樣。因此，如果給定系統函式的實部(虛部），就不能任意確定虛部（實部），否則就不能保證是因果系統。同理，一個穩定的最小相位系統，由於其對數幅度1og|H(Ω)|和對數相位arg〔H(Ω))〕之間互為希爾伯特變換，則該系統一定是因果系統。所以通常設計濾波器，當給定幅頻特性後，則其相頻特性就不能任意選擇。否則，不能保證系統是穩定和因果的。理想的希爾伯特變換器是非因果系統，採用數位訊號處理技術，將信號適當延遲，比較容易實現在一定頻帶範圍內，頻率特性是近似理想的。
希爾伯特變換定義如下：
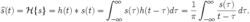hilbert其中
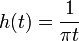希爾伯特變換並考慮此積分為柯西主值(Cauchy principal value)，其避免掉在τ=t以及τ=±∞等處的奇點。
頻率回響
希爾伯特變換之頻率回響由傅立葉變換給出：
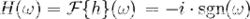Hw其中F是傅立葉變換，i(有時寫作j)是虛數單位，ω是角頻率，以及
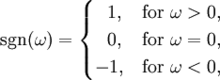sgn常被稱作signum函式。既然：
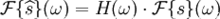Fs希爾伯特實際上是一個使相位滯後pi/2的全通移相網路。
我們也注意到：H^2(\omega) = -1。因此將上面方程式乘上，可得到：
從中，可以看出反（逆）希爾伯特變換
存在原因
概述
在地震三瞬分析中希爾伯特變換存在的問題
通過希爾伯特變換，使得我們對簡訊號和複雜信號的瞬時參數的定義及計算成為可能，能夠實現真正意義上的瞬時信號的提取，因而希爾伯特變換在信號處理上具有十分重要的地位。然而，它也存在以下問題：
原因一
希爾伯特變換隻能近似套用於窄帶信號，即只適用 的信號，其中B(B為信號頻寬)。但實際套用中，存在許多非窄帶信號，希爾伯特變換對這些信號無能為力。即便是窄帶信號，如果不能完全滿足希爾伯特變換條件，也會使結果發生錯誤。而實際信號中由於噪聲的存在，會使很多原來滿足希爾伯特變換條件的信號無法完全滿足；
原因二
對於任意給定t時刻，通過希爾伯特變換運算後的結果只能存在一個頻率值，即只能處理任何時刻為單一頻率的信號；
對於一個非平穩的數據序列，希爾伯特變換得到的結果很大程度上失去了原有的物理意義。
